第12章 整式的乘除单元测试题 2021——2022学年华东师大版八年级数学上册(word版含解析)
文档属性
| 名称 | 第12章 整式的乘除单元测试题 2021——2022学年华东师大版八年级数学上册(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 196.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 13:59:01 | ||
图片预览



文档简介
第12章 整式的乘除
一、选择题(每题3分,共24分)
1.下列运算中正确的是( )
A.a5+a5=a10 B.a7÷a=a6
C.a3·a2=a6 D.(-a3)2=-a6
2.下列计算正确的是( )
A.(a4b)3=a7b3
B.-2b(4a-b2)=-8ab-2b3
C.a·a3+a2·a2=2a4
D.(a-5)2=a2-25
3.若(x-2y)2=(x+2y)2+m,则m等于( )
A.4xy B.-4xy C.8xy D.-8xy
4.下列因式分解正确的是( )
A.x2-x=x(x+1)
B.a2-3a-4=(a+4)(a-1)
C.a2+2ab-b2=(a-b)2
D.x2-y2=(x+y)(x-y)
5.边长为a的正方形,其边长减少b后,所得正方形的面积比原正方形的面积减少( )
A.a2 B.b2 C.(a-b)2 D.2ab-b2
6.对于任意非零整数n,按图1所示的程序计算应输出的答案为( )
n→平方→+2n→÷n→-n→答案
图1
A.n2-n+2 B.3-n
C.n2-2 D.2
7.已知长方形的面积为4a2-6ab+2a,且它的一边长为2a,则其周长为( )
A.4a-3b B.8a-6b
C.4a-3b-1 D.8a-6b+2
8.已知10x=m,10y=n,则102x+3y等于( )
A.2m+3n B.m2+n2 C.6mn D.m2n3
二、填空题(每题4分,共24分)
9.因式分解:a2+ab-a= .?
10.计算:(-12)2021×= .?
11.若x2+2x+m恰好可以写成一个多项式的平方,则m= .?
12.若2m×8n=32,2m÷4n=16,则m+n的值为 .?
13.若x2-2x-2=0,则(2x+3)(x-2)-3x= .?
14.分解因式:(x-y)2-6x+6y+9= .?
三、解答题(共52分)
15.(6分)计算:
(1)x(x2+x-1)-(2x2-1)(x-4);
(2)[5xy2(x2-3xy)+(3x2y2)3]÷(5xy)2.
16.(6分)把下列多项式分解因式:
(1)(x-1)2+2(x-5);
(2)-ab(a-b)2+a(b-a)2.
17.(6分)先化简,再求值:(3x+2)(3x-2)+(x-2)2-5x(x-1),其中x=-1.
18.(8分)凤燕与丽君做游戏,两人各报一个整式,丽君报的整式作为除式,凤燕报的整式作为被除式,要求商式必须是4x2y.
(1)若凤燕报的整式是x7y5-4x5y4+16x2y,则丽君报的整式是什么?
(2)若凤燕报的整式是(-2x3y2)2+5x3y2,则丽君能报出一个整式吗?请说明理由.
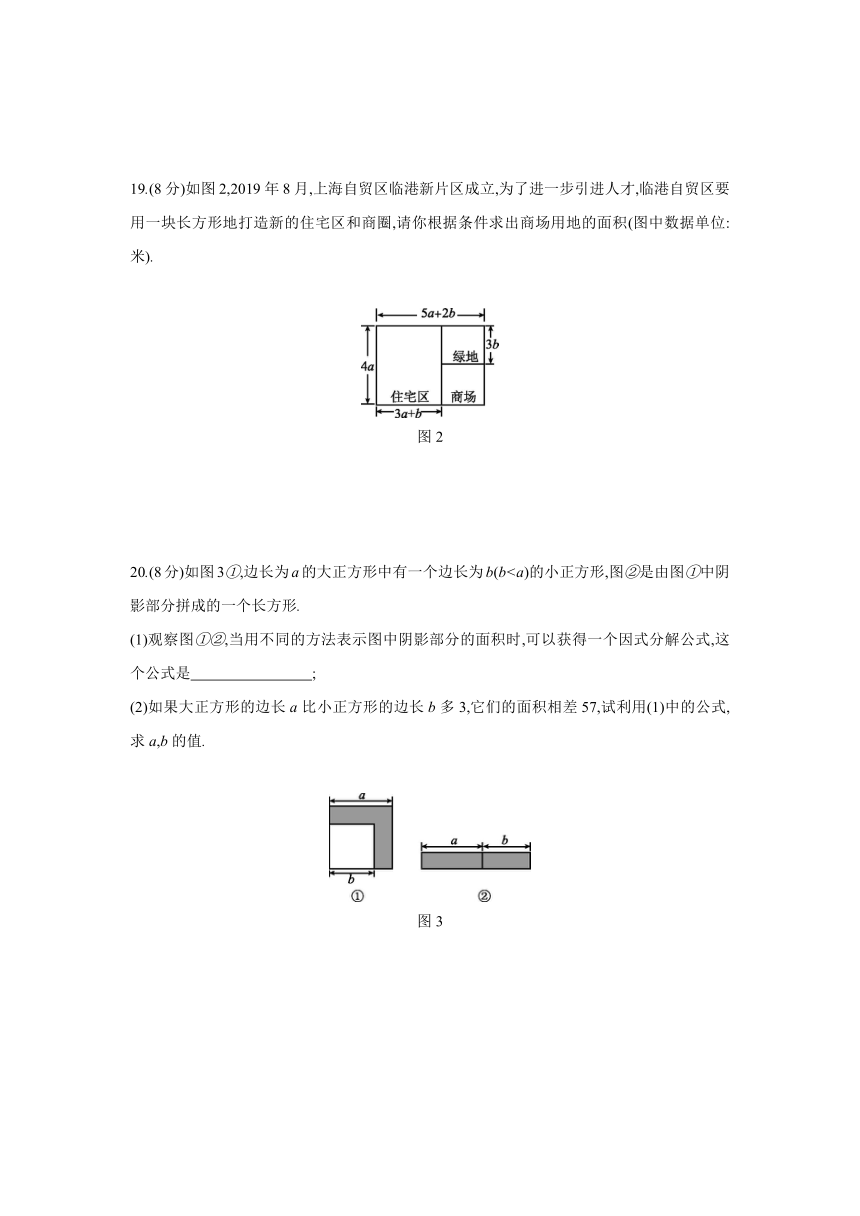
19.(8分)如图2,2019年8月,上海自贸区临港新片区成立,为了进一步引进人才,临港自贸区要用一块长方形地打造新的住宅区和商圈,请你根据条件求出商场用地的面积(图中数据单位:米).
图2
20.(8分)如图3①,边长为a的大正方形中有一个边长为b(b(1)观察图①②,当用不同的方法表示图中阴影部分的面积时,可以获得一个因式分解公式,这个公式是 ;?
(2)如果大正方形的边长a比小正方形的边长b多3,它们的面积相差57,试利用(1)中的公式,求a,b的值.
图3
21.(10分)定义新运算:对于任意实数a,b,都有a⊕b=(a+b)(a-b)+2b(a+b),等式右边是通常的加法、减法及乘法运算.例如:2⊕5=(2+5)×(2-5)+2×5×(2+5)=-21+70=49.
(1)求(-2)⊕3的值;
(2)通过计算,验证等式a⊕b=b⊕a成立.
答案
1.B [解析] a5+a5=2a5,故A不符合题意;
a7÷a=a6,故B符合题意;
a3·a2=a5,故C不符合题意;
(-a3)2=a6,故D不符合题意.
故选B.
2.C [解析] (a4b)3=a12b3,故A不符合题意;-2b(4a-b2)=-8ab+2b3,故B不符合题意;a·a3+a2·a2=2a4,故C符合题意;(a-5)2=a2-10a+25,故D不符合题意.故选C.
3.D [解析] 将等式两边分别展开,两边对应相等,进而求得m.
4.D [解析] x2-x=x(x-1),故A错误;
a2-3a-4=(a-4)(a+1),故B错误;
a2+2ab-b2不能分解因式,故C错误;
x2-y2=(x+y)(x-y),故D正确.
故选D.
5.D [解析] 原正方形的面积为a2,新正方形的面积为(a-b)2,所以新正方形的面积比原正方形的面积减少a2-(a-b)2=[a+(a-b)][a-(a-b)]=(a+a-b)(a-a+b)=b(2a-b)=2ab-b2.
6.D [解析] 运算过程如下:(n2+2n)÷n-n=n(n+2)÷n-n=n+2-n=2.
7.D [解析] 另一边长为(4a2-6ab+2a)÷2a=2a-3b+1,
所以其周长为2·2a+2(2a-3b+1)=8a-6b+2.
8.D [解析] 102x+3y=102x·103y=(10x)2·(10y)3=m2n3.故选D.
9.a(a+b-1)
10.144 [解析] (-12)2021×
=(-12)2×(-12)2019×
=(-12)2×
=(-12)2=144.
故答案为144.
11.1
12. [解析] 因为2m×8n=2m×23n=2m+3n=32=25,2m÷4n=2m÷22n=2m-2n=16=24,
所以m+3n=5,m-2n=4,
两式相加,得2m+n=9,
则原式=(2m+n)=.
故答案为.
13.-2 [解析] 因为x2-2x-2=0,所以x2-2x=2,
所以(2x+3)(x-2)-3x=2x2-x-6-3x=2x2-4x-6=2(x2-2x)-6=4-6=-2.
14.(x-y-3)2 [解析] 观察题中的特点,把-6x+6y提取公因式-6以后变成了-6(x-y),若将(x-y)看成一个整体,就可以套两数差的平方公式进行因式分解了.
(x-y)2-6x+6y+9=(x-y)2-6(x-y)+9=(x-y-3)2.
15.解:(1)原式=x3+x2-x-(2x3-8x2-x+4)
=x3+x2-x-2x3+8x2+x-4
=-x3+9x2-4.
(2)[5xy2(x2-3xy)+(3x2y2)3]÷(5xy)2
=(5x3y2-15x2y3+27x6y6)÷25x2y2
=x-y+x4y4.
16.解:(1)原式=x2-2x+1+2x-10=x2-9=(x+3)(x-3).
(2)-ab(a-b)2+a(b-a)2
=-ab(a-b)2+a(a-b)2
=-a(a-b)2(b-1).
17.解:原式=9x2-4+x2-4x+4-5x2+5x
=5x2+x.
当x=-1时,
原式=5×(-1)2+(-1)=5-1=4.
18.解:(1)丽君报的整式为(x7y5-4x5y4+16x2y)÷4x2y=x5y4-x3y3+4.
(2)丽君能报出一个整式.
理由:[(-2x3y2)2+5x3y2]÷4x2y=(4x6y4+5x3y2)÷4x2y=x4y3+xy,
即丽君能报出一个整式,为x4y3+xy.
19.解:由题意可得[(5a+2b)-(3a+b)]·(4a-3b)
=(5a+2b-3a-b)(4a-3b)
=(2a+b)(4a-3b)
=8a2-2ab-3b2,
则商场用地的面积是(8a2-2ab-3b2)平方米.
20.解:(1)a2-b2=(a+b)(a-b)
[解析] 由图①可得阴影部分的面积=a2-b2,由图②可得阴影部分的面积=(a-b)(a+b),
所以可得公式为a2-b2=(a+b)(a-b).
故答案为a2-b2=(a+b)(a-b).
(2)由题意,得a-b=3,a2-b2=57.
因为a2-b2=(a+b)(a-b)=57,
所以a+b=19,
所以解得
所以a,b的值分别是11,8.
21.解:(1)-2⊕3
=(-2+3)×(-2-3)+2×3×(-2+3)
=1×(-5)+2×3×1
=-5+6=1.
(2)因为a⊕b
=(a+b)(a-b)+2b(a+b)
=a2-b2+2ab+2b2=(a+b)2,
b⊕a
=(b+a)(b-a)+2a(b+a)
=b2-a2+2ab+2a2
=(a+b)2,
所以a⊕b=b⊕a成立.
一、选择题(每题3分,共24分)
1.下列运算中正确的是( )
A.a5+a5=a10 B.a7÷a=a6
C.a3·a2=a6 D.(-a3)2=-a6
2.下列计算正确的是( )
A.(a4b)3=a7b3
B.-2b(4a-b2)=-8ab-2b3
C.a·a3+a2·a2=2a4
D.(a-5)2=a2-25
3.若(x-2y)2=(x+2y)2+m,则m等于( )
A.4xy B.-4xy C.8xy D.-8xy
4.下列因式分解正确的是( )
A.x2-x=x(x+1)
B.a2-3a-4=(a+4)(a-1)
C.a2+2ab-b2=(a-b)2
D.x2-y2=(x+y)(x-y)
5.边长为a的正方形,其边长减少b后,所得正方形的面积比原正方形的面积减少( )
A.a2 B.b2 C.(a-b)2 D.2ab-b2
6.对于任意非零整数n,按图1所示的程序计算应输出的答案为( )
n→平方→+2n→÷n→-n→答案
图1
A.n2-n+2 B.3-n
C.n2-2 D.2
7.已知长方形的面积为4a2-6ab+2a,且它的一边长为2a,则其周长为( )
A.4a-3b B.8a-6b
C.4a-3b-1 D.8a-6b+2
8.已知10x=m,10y=n,则102x+3y等于( )
A.2m+3n B.m2+n2 C.6mn D.m2n3
二、填空题(每题4分,共24分)
9.因式分解:a2+ab-a= .?
10.计算:(-12)2021×= .?
11.若x2+2x+m恰好可以写成一个多项式的平方,则m= .?
12.若2m×8n=32,2m÷4n=16,则m+n的值为 .?
13.若x2-2x-2=0,则(2x+3)(x-2)-3x= .?
14.分解因式:(x-y)2-6x+6y+9= .?
三、解答题(共52分)
15.(6分)计算:
(1)x(x2+x-1)-(2x2-1)(x-4);
(2)[5xy2(x2-3xy)+(3x2y2)3]÷(5xy)2.
16.(6分)把下列多项式分解因式:
(1)(x-1)2+2(x-5);
(2)-ab(a-b)2+a(b-a)2.
17.(6分)先化简,再求值:(3x+2)(3x-2)+(x-2)2-5x(x-1),其中x=-1.
18.(8分)凤燕与丽君做游戏,两人各报一个整式,丽君报的整式作为除式,凤燕报的整式作为被除式,要求商式必须是4x2y.
(1)若凤燕报的整式是x7y5-4x5y4+16x2y,则丽君报的整式是什么?
(2)若凤燕报的整式是(-2x3y2)2+5x3y2,则丽君能报出一个整式吗?请说明理由.
19.(8分)如图2,2019年8月,上海自贸区临港新片区成立,为了进一步引进人才,临港自贸区要用一块长方形地打造新的住宅区和商圈,请你根据条件求出商场用地的面积(图中数据单位:米).
图2
20.(8分)如图3①,边长为a的大正方形中有一个边长为b(b
(2)如果大正方形的边长a比小正方形的边长b多3,它们的面积相差57,试利用(1)中的公式,求a,b的值.
图3
21.(10分)定义新运算:对于任意实数a,b,都有a⊕b=(a+b)(a-b)+2b(a+b),等式右边是通常的加法、减法及乘法运算.例如:2⊕5=(2+5)×(2-5)+2×5×(2+5)=-21+70=49.
(1)求(-2)⊕3的值;
(2)通过计算,验证等式a⊕b=b⊕a成立.
答案
1.B [解析] a5+a5=2a5,故A不符合题意;
a7÷a=a6,故B符合题意;
a3·a2=a5,故C不符合题意;
(-a3)2=a6,故D不符合题意.
故选B.
2.C [解析] (a4b)3=a12b3,故A不符合题意;-2b(4a-b2)=-8ab+2b3,故B不符合题意;a·a3+a2·a2=2a4,故C符合题意;(a-5)2=a2-10a+25,故D不符合题意.故选C.
3.D [解析] 将等式两边分别展开,两边对应相等,进而求得m.
4.D [解析] x2-x=x(x-1),故A错误;
a2-3a-4=(a-4)(a+1),故B错误;
a2+2ab-b2不能分解因式,故C错误;
x2-y2=(x+y)(x-y),故D正确.
故选D.
5.D [解析] 原正方形的面积为a2,新正方形的面积为(a-b)2,所以新正方形的面积比原正方形的面积减少a2-(a-b)2=[a+(a-b)][a-(a-b)]=(a+a-b)(a-a+b)=b(2a-b)=2ab-b2.
6.D [解析] 运算过程如下:(n2+2n)÷n-n=n(n+2)÷n-n=n+2-n=2.
7.D [解析] 另一边长为(4a2-6ab+2a)÷2a=2a-3b+1,
所以其周长为2·2a+2(2a-3b+1)=8a-6b+2.
8.D [解析] 102x+3y=102x·103y=(10x)2·(10y)3=m2n3.故选D.
9.a(a+b-1)
10.144 [解析] (-12)2021×
=(-12)2×(-12)2019×
=(-12)2×
=(-12)2=144.
故答案为144.
11.1
12. [解析] 因为2m×8n=2m×23n=2m+3n=32=25,2m÷4n=2m÷22n=2m-2n=16=24,
所以m+3n=5,m-2n=4,
两式相加,得2m+n=9,
则原式=(2m+n)=.
故答案为.
13.-2 [解析] 因为x2-2x-2=0,所以x2-2x=2,
所以(2x+3)(x-2)-3x=2x2-x-6-3x=2x2-4x-6=2(x2-2x)-6=4-6=-2.
14.(x-y-3)2 [解析] 观察题中的特点,把-6x+6y提取公因式-6以后变成了-6(x-y),若将(x-y)看成一个整体,就可以套两数差的平方公式进行因式分解了.
(x-y)2-6x+6y+9=(x-y)2-6(x-y)+9=(x-y-3)2.
15.解:(1)原式=x3+x2-x-(2x3-8x2-x+4)
=x3+x2-x-2x3+8x2+x-4
=-x3+9x2-4.
(2)[5xy2(x2-3xy)+(3x2y2)3]÷(5xy)2
=(5x3y2-15x2y3+27x6y6)÷25x2y2
=x-y+x4y4.
16.解:(1)原式=x2-2x+1+2x-10=x2-9=(x+3)(x-3).
(2)-ab(a-b)2+a(b-a)2
=-ab(a-b)2+a(a-b)2
=-a(a-b)2(b-1).
17.解:原式=9x2-4+x2-4x+4-5x2+5x
=5x2+x.
当x=-1时,
原式=5×(-1)2+(-1)=5-1=4.
18.解:(1)丽君报的整式为(x7y5-4x5y4+16x2y)÷4x2y=x5y4-x3y3+4.
(2)丽君能报出一个整式.
理由:[(-2x3y2)2+5x3y2]÷4x2y=(4x6y4+5x3y2)÷4x2y=x4y3+xy,
即丽君能报出一个整式,为x4y3+xy.
19.解:由题意可得[(5a+2b)-(3a+b)]·(4a-3b)
=(5a+2b-3a-b)(4a-3b)
=(2a+b)(4a-3b)
=8a2-2ab-3b2,
则商场用地的面积是(8a2-2ab-3b2)平方米.
20.解:(1)a2-b2=(a+b)(a-b)
[解析] 由图①可得阴影部分的面积=a2-b2,由图②可得阴影部分的面积=(a-b)(a+b),
所以可得公式为a2-b2=(a+b)(a-b).
故答案为a2-b2=(a+b)(a-b).
(2)由题意,得a-b=3,a2-b2=57.
因为a2-b2=(a+b)(a-b)=57,
所以a+b=19,
所以解得
所以a,b的值分别是11,8.
21.解:(1)-2⊕3
=(-2+3)×(-2-3)+2×3×(-2+3)
=1×(-5)+2×3×1
=-5+6=1.
(2)因为a⊕b
=(a+b)(a-b)+2b(a+b)
=a2-b2+2ab+2b2=(a+b)2,
b⊕a
=(b+a)(b-a)+2a(b+a)
=b2-a2+2ab+2a2
=(a+b)2,
所以a⊕b=b⊕a成立.
