7.3平行线的判定练习题 -2021——2022学年北师大版八年级数学上册(Word版含答案)
文档属性
| 名称 | 7.3平行线的判定练习题 -2021——2022学年北师大版八年级数学上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 138.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 16:48:28 | ||
图片预览

文档简介
3 平行线的判定
【基础练习】
知识点 平行线的判定
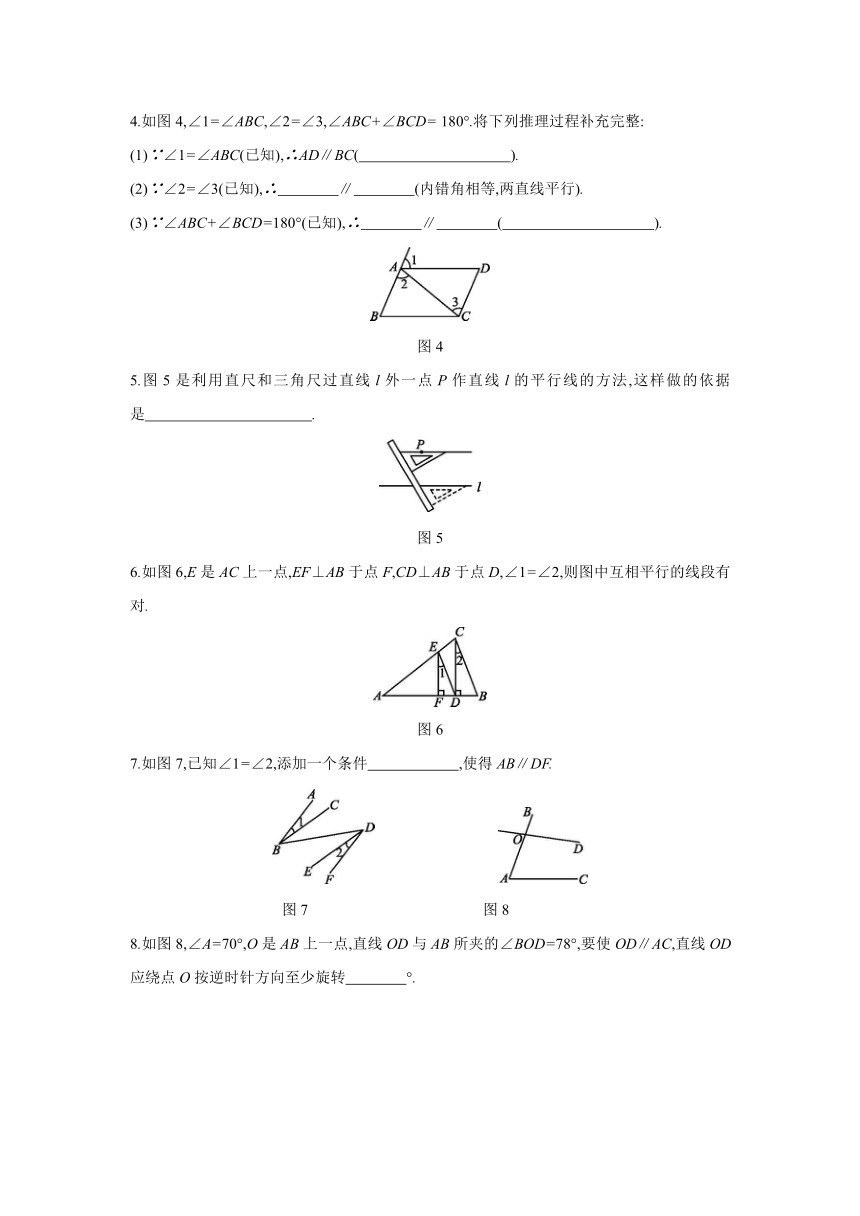
1.如图1,∠1=50°,∠2=70°,∠3=60°,下列条件能得到DE∥BC的是( )
图1
A.∠B=60°
B.∠C=60°
C.∠B=70°
D.∠C=70°
2.如图2,下列不能判定AB∥CD的是( )
图2
A.∠B=∠DCE
B.∠A=∠ACD
C.∠B+∠BCD=180°
D.∠A=∠DCE
3.如图3,下列推论及所注理由正确的是( )
图3
A.∵∠1=∠B,∴DE∥BC(内错角相等,两直线平行)
B.∵∠2=∠C,∴DE∥BC(同位角相等,两直线平行)
C.∵∠BAE+∠B=180°,∴DE∥BC(同旁内角互补,两直线平行)
D.∵∠3=∠1,∴DE∥BC(对顶角相等)
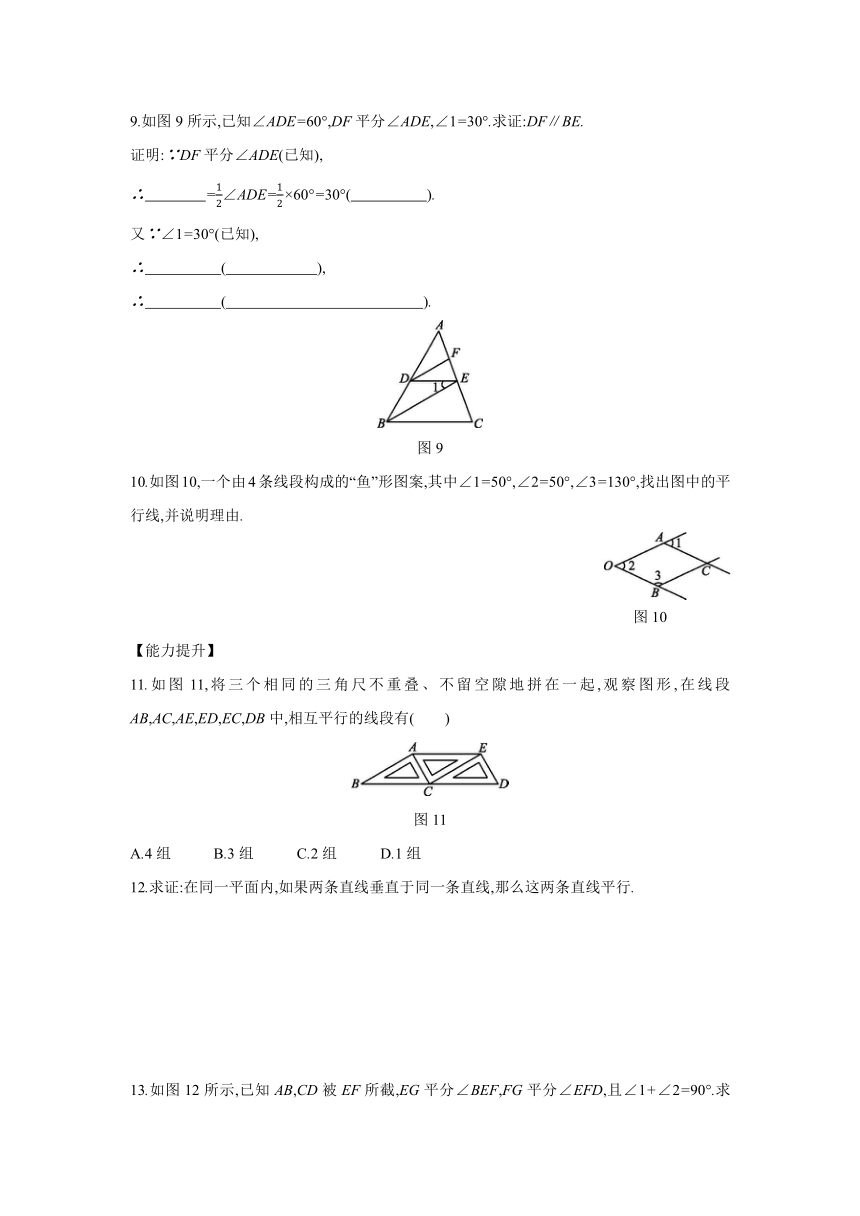
4.如图4,∠1=∠ABC,∠2=∠3,∠ABC+∠BCD=
180°.将下列推理过程补充完整:
(1)∵∠1=∠ABC(已知),∴AD∥BC( ).?
(2)∵∠2=∠3(已知),∴ ∥ (内错角相等,两直线平行).?
(3)∵∠ABC+∠BCD=180°(已知),∴ ∥ ( ).?
图4
5.图5是利用直尺和三角尺过直线l外一点P作直线l的平行线的方法,这样做的依据是 .?
图5
6.如图6,E是AC上一点,EF⊥AB于点F,CD⊥AB于点D,∠1=∠2,则图中互相平行的线段有 对.?
图6
7.如图7,已知∠1=∠2,添加一个条件 ,使得AB∥DF.?
图7
图8
8.如图8,∠A=70°,O是AB上一点,直线OD与AB所夹的∠BOD=78°,要使OD∥AC,直线OD应绕点O按逆时针方向至少旋转 °.?
9.如图9所示,已知∠ADE=60°,DF平分∠ADE,∠1=30°.求证:DF∥BE.
证明:∵DF平分∠ADE(已知),
∴ =∠ADE=×60°=30°( ).?
又∵∠1=30°(已知),
∴ ( ),?
∴ ( ).?
图9
10.如图10,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
图10
【能力提升】
11.如图11,将三个相同的三角尺不重叠、不留空隙地拼在一起,观察图形,在线段AB,AC,AE,ED,EC,DB中,相互平行的线段有( )
图11
A.4组
B.3组
C.2组
D.1组
12.求证:在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线平行.
13.如图12所示,已知AB,CD被EF所截,EG平分∠BEF,FG平分∠EFD,且∠1+∠2=90°.求证:AB∥CD.
图12
14.已知:如图13,直线AB,CD与直线EF分别相交于点M和点N,MP平分∠AMF,NQ平分∠END,∠AME=∠DNF.求证:MP∥NQ.
图13
15.如图14所示,EB⊥MN于点B,FD⊥MN于点D,∠1=∠2.AB与CD是否平行?请说明理由.
图14
16.如图15,台球运动中,台桌为一个长方形DEFG,如果母球P击中点A,经桌边反弹后击中相邻的另一桌边上的点B,再次反弹经过点C.
(1)若∠PAD=32°,求∠PAB的度数;
(2)母球P经过的路线BC与PA一定平行吗?请说明理由.
图15
答案
1.B
2.D
3.C
4.(1)同位角相等,两直线平行
(2)AB CD
(3)AB CD 同旁内角互补,两直线平行
5.同位角相等,两直线平行
6.2 [解析]
因为EF⊥AB,CD⊥AB,所以∠EFA=∠CDA=90°,所以EF∥CD,所以∠1=∠EDC.因为∠1=∠2,所以∠EDC=∠2,所以DE∥BC,即图中互相平行的线段有2对.
7.∠CBD=∠BDE(答案不唯一)
[解析]
∵∠1=∠2,∠CBD=∠BDE,∴∠1+∠CBD=∠2+∠BDE,即∠ABD=∠FDB,∴AB∥DF.
8.8
9.∠FDE 角平分线的性质 ∠FDE=∠1
等量代换 DF∥BE 内错角相等,两直线平行
10.解:OB∥AC,OA∥BC.理由:∵∠1=50°,∠2=50°,∴∠1=∠2,∴OB∥AC(同位角相等,两直线平行).∵∠2=50°,∠3=130°,∴∠2+∠3=180°,∴OA∥BC(同旁内角互补,两直线平行).
11.B [解析]
∠B=∠DCE,则AB∥EC(同位角相等,两直线平行);∠BCA=∠CAE,则AE∥DB(内错角相等,两直线平行);∠ACE=∠DEC,则AC∥ED(内错角相等,两直线平行).故相互平行的线段有AB∥EC,AE∥DB,AC∥ED,共有3组.故选B.
12.解:已知:如图,AB⊥EF,垂足为B,CD⊥EF,垂足为D.求证:AB∥CD.
证明:∵AB⊥EF,CD⊥EF,∴∠ABD=∠CDF=90°,∴AB∥CD.
13.证明:因为EG平分∠BEF(已知),
所以∠BEF=2∠1(角平分线的性质).
同理可证∠EFD=2∠2.
又因为∠1+∠2=90°(已知),
所以∠BEF+∠EFD=180°(等式的性质).
所以AB∥CD(同旁内角互补,两直线平行).
14.证明:∵∠AME=∠DNF(已知),
∠AME+∠AMN=∠DNF+∠DNM=180°(平角的定义),
∴∠AMN=∠DNM(等式的性质).
∵MP平分∠AMF,NQ平分∠END,
∴∠PMN=∠AMN,∠QNM=∠DNM(角平分线的性质),
∴∠PMN=∠QNM(等量代换),
∴MP∥NQ(内错角相等,两直线平行).
15.解:AB∥CD.理由如下:
因为EB⊥MN,FD⊥MN,
所以∠EBM=∠FDM=90°(垂直的性质).
又因为∠1=∠2(已知),
所以∠EBM-∠1=∠FDM-∠2,
即∠ABM=∠CDM,
所以AB∥CD(同位角相等,两直线平行).
16.解:(1)∵∠PAD=32°,∠PAD=∠BAE,∠PAD+∠PAB+∠BAE=180°,
∴∠PAB=180°-32°-32°=116°.
(2)BC∥PA.理由如下:
∵∠PAD=∠BAE,
∠PAB=180°-∠PAD-∠BAE,
∴∠PAB=180°-2∠BAE.
同理:∠ABC=180°-2∠ABE.
∵∠BAE+∠ABE=90°,
∴∠PAB+∠ABC=360°-2(∠BAE+∠ABE)=180°,
∴BC∥PA.
【基础练习】
知识点 平行线的判定
1.如图1,∠1=50°,∠2=70°,∠3=60°,下列条件能得到DE∥BC的是( )
图1
A.∠B=60°
B.∠C=60°
C.∠B=70°
D.∠C=70°
2.如图2,下列不能判定AB∥CD的是( )
图2
A.∠B=∠DCE
B.∠A=∠ACD
C.∠B+∠BCD=180°
D.∠A=∠DCE
3.如图3,下列推论及所注理由正确的是( )
图3
A.∵∠1=∠B,∴DE∥BC(内错角相等,两直线平行)
B.∵∠2=∠C,∴DE∥BC(同位角相等,两直线平行)
C.∵∠BAE+∠B=180°,∴DE∥BC(同旁内角互补,两直线平行)
D.∵∠3=∠1,∴DE∥BC(对顶角相等)
4.如图4,∠1=∠ABC,∠2=∠3,∠ABC+∠BCD=
180°.将下列推理过程补充完整:
(1)∵∠1=∠ABC(已知),∴AD∥BC( ).?
(2)∵∠2=∠3(已知),∴ ∥ (内错角相等,两直线平行).?
(3)∵∠ABC+∠BCD=180°(已知),∴ ∥ ( ).?
图4
5.图5是利用直尺和三角尺过直线l外一点P作直线l的平行线的方法,这样做的依据是 .?
图5
6.如图6,E是AC上一点,EF⊥AB于点F,CD⊥AB于点D,∠1=∠2,则图中互相平行的线段有 对.?
图6
7.如图7,已知∠1=∠2,添加一个条件 ,使得AB∥DF.?
图7
图8
8.如图8,∠A=70°,O是AB上一点,直线OD与AB所夹的∠BOD=78°,要使OD∥AC,直线OD应绕点O按逆时针方向至少旋转 °.?
9.如图9所示,已知∠ADE=60°,DF平分∠ADE,∠1=30°.求证:DF∥BE.
证明:∵DF平分∠ADE(已知),
∴ =∠ADE=×60°=30°( ).?
又∵∠1=30°(已知),
∴ ( ),?
∴ ( ).?
图9
10.如图10,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
图10
【能力提升】
11.如图11,将三个相同的三角尺不重叠、不留空隙地拼在一起,观察图形,在线段AB,AC,AE,ED,EC,DB中,相互平行的线段有( )
图11
A.4组
B.3组
C.2组
D.1组
12.求证:在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线平行.
13.如图12所示,已知AB,CD被EF所截,EG平分∠BEF,FG平分∠EFD,且∠1+∠2=90°.求证:AB∥CD.
图12
14.已知:如图13,直线AB,CD与直线EF分别相交于点M和点N,MP平分∠AMF,NQ平分∠END,∠AME=∠DNF.求证:MP∥NQ.
图13
15.如图14所示,EB⊥MN于点B,FD⊥MN于点D,∠1=∠2.AB与CD是否平行?请说明理由.
图14
16.如图15,台球运动中,台桌为一个长方形DEFG,如果母球P击中点A,经桌边反弹后击中相邻的另一桌边上的点B,再次反弹经过点C.
(1)若∠PAD=32°,求∠PAB的度数;
(2)母球P经过的路线BC与PA一定平行吗?请说明理由.
图15
答案
1.B
2.D
3.C
4.(1)同位角相等,两直线平行
(2)AB CD
(3)AB CD 同旁内角互补,两直线平行
5.同位角相等,两直线平行
6.2 [解析]
因为EF⊥AB,CD⊥AB,所以∠EFA=∠CDA=90°,所以EF∥CD,所以∠1=∠EDC.因为∠1=∠2,所以∠EDC=∠2,所以DE∥BC,即图中互相平行的线段有2对.
7.∠CBD=∠BDE(答案不唯一)
[解析]
∵∠1=∠2,∠CBD=∠BDE,∴∠1+∠CBD=∠2+∠BDE,即∠ABD=∠FDB,∴AB∥DF.
8.8
9.∠FDE 角平分线的性质 ∠FDE=∠1
等量代换 DF∥BE 内错角相等,两直线平行
10.解:OB∥AC,OA∥BC.理由:∵∠1=50°,∠2=50°,∴∠1=∠2,∴OB∥AC(同位角相等,两直线平行).∵∠2=50°,∠3=130°,∴∠2+∠3=180°,∴OA∥BC(同旁内角互补,两直线平行).
11.B [解析]
∠B=∠DCE,则AB∥EC(同位角相等,两直线平行);∠BCA=∠CAE,则AE∥DB(内错角相等,两直线平行);∠ACE=∠DEC,则AC∥ED(内错角相等,两直线平行).故相互平行的线段有AB∥EC,AE∥DB,AC∥ED,共有3组.故选B.
12.解:已知:如图,AB⊥EF,垂足为B,CD⊥EF,垂足为D.求证:AB∥CD.
证明:∵AB⊥EF,CD⊥EF,∴∠ABD=∠CDF=90°,∴AB∥CD.
13.证明:因为EG平分∠BEF(已知),
所以∠BEF=2∠1(角平分线的性质).
同理可证∠EFD=2∠2.
又因为∠1+∠2=90°(已知),
所以∠BEF+∠EFD=180°(等式的性质).
所以AB∥CD(同旁内角互补,两直线平行).
14.证明:∵∠AME=∠DNF(已知),
∠AME+∠AMN=∠DNF+∠DNM=180°(平角的定义),
∴∠AMN=∠DNM(等式的性质).
∵MP平分∠AMF,NQ平分∠END,
∴∠PMN=∠AMN,∠QNM=∠DNM(角平分线的性质),
∴∠PMN=∠QNM(等量代换),
∴MP∥NQ(内错角相等,两直线平行).
15.解:AB∥CD.理由如下:
因为EB⊥MN,FD⊥MN,
所以∠EBM=∠FDM=90°(垂直的性质).
又因为∠1=∠2(已知),
所以∠EBM-∠1=∠FDM-∠2,
即∠ABM=∠CDM,
所以AB∥CD(同位角相等,两直线平行).
16.解:(1)∵∠PAD=32°,∠PAD=∠BAE,∠PAD+∠PAB+∠BAE=180°,
∴∠PAB=180°-32°-32°=116°.
(2)BC∥PA.理由如下:
∵∠PAD=∠BAE,
∠PAB=180°-∠PAD-∠BAE,
∴∠PAB=180°-2∠BAE.
同理:∠ABC=180°-2∠ABE.
∵∠BAE+∠ABE=90°,
∴∠PAB+∠ABC=360°-2(∠BAE+∠ABE)=180°,
∴BC∥PA.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
