7.5 第1课时 三角形内角和定理的证明练习题 2021——2022学年北师大版八年级数学上册
文档属性
| 名称 | 7.5 第1课时 三角形内角和定理的证明练习题 2021——2022学年北师大版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 142.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 20:04:31 | ||
图片预览


文档简介
5 第1课时 三角形内角和定理的证明
【基础练习】
知识点
三角形内角和定理
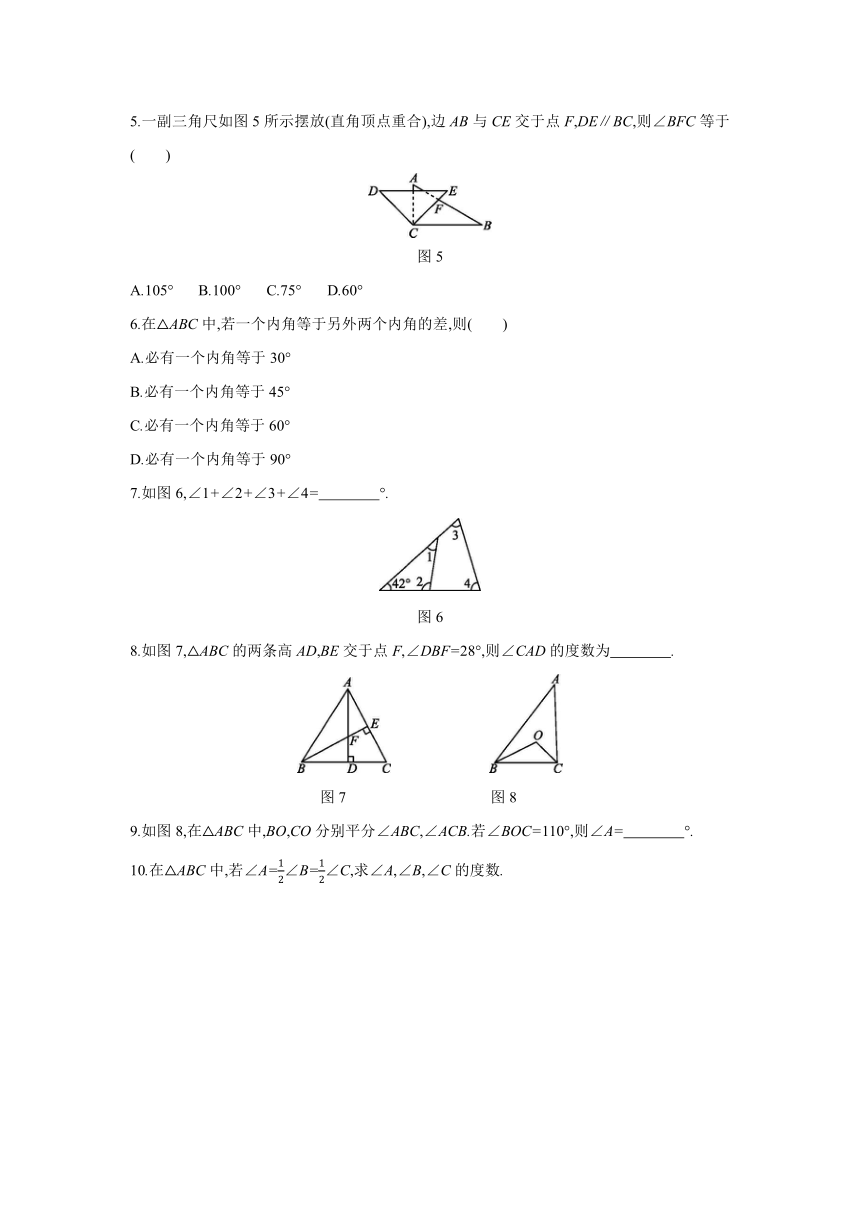
1.如图1,在△ABC中,∠A=60°,∠B=40°,则∠C等于( )
图1
A.100°
B.80°
C.60°
D.40°
2.[教材随堂练习第3题变式]
如图2,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的度数为( )
图2
A.54°
B.62°
C.64°
D.74°
3.如图3,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为( )
图3
A.40°
B.45°
C.50°
D.55°
4.如图4,直线l1∥l2,直线l3与l1,l2分别交于点A,C,BC⊥l3交l1于点B.若∠1=70°,则∠2的度数为( )
图4
A.10°
B.20°
C.30°
D.40°
5.一副三角尺如图5所示摆放(直角顶点重合),边AB与CE交于点F,DE∥BC,则∠BFC等于( )
图5
A.105°
B.100°
C.75°
D.60°
6.在△ABC中,若一个内角等于另外两个内角的差,则( )
A.必有一个内角等于30°
B.必有一个内角等于45°
C.必有一个内角等于60°
D.必有一个内角等于90°
7.如图6,∠1+∠2+∠3+∠4= °.?
图6
8.如图7,△ABC的两条高AD,BE交于点F,∠DBF=28°,则∠CAD的度数为 .?
图7
图8
9.如图8,在△ABC中,BO,CO分别平分∠ABC,∠ACB.若∠BOC=110°,则∠A= °.?
10.在△ABC中,若∠A=∠B=∠C,求∠A,∠B,∠C的度数.
11.如图9,在△ABC中,∠C=92°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P,∠BDC=58°,求∠BAP的度数.
图9
12.如图10,在△ABC中,∠B=∠C,F为AC上一点,FD⊥BC于点D,DE⊥AB于点E,∠A=56°,求∠EDF的度数.
图10
【能力提升】
13.如图11,在△ABC中,∠B+∠C=100°,AD平分∠BAC交BC于点D,DE∥AB交AC于点E,则∠ADE的度数是( )
图11
A.30°
B.40°
C.50°
D.60°
14.如图12,在△ABC中,BC边不动,点A竖直向上运动,则∠A越来越小,∠B,∠C越来越大.若∠A减小α度,∠B增加β度,∠C增加γ度,则α,β,γ三者之间的等量关系是 .?
图12
15.如图13,在△ABC中,∠A=70°,∠B=50°,D,E分别为AB,AC上的点,沿DE折叠△ABC使点A落在BC边上的点F处.若△EFC为直角三角形,则∠BDF的度数为 .?
图13
16.如图14所示,在△ABC中,已知∠C>∠B,AD⊥BC于点D,AE平分∠BAC交BC于点E.
(1)若∠C=60°,∠B=44°,求∠EAD的度数;
(2)猜想∠EAD与(∠C-∠B)的关系,并说明理由.
图14
17.如图15(a),线段AB,CD相交于点O,连接AD,CB,我们把这样的图形称为“8字形”.
(1)请直接写出图(a)中∠A,∠B,∠C,∠D之间的数量关系: .?
(2)如图(b),在图(a)的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并分别与CD,AB相交于点M,N.
①图(b)中“8字形”有 个;?
②在图(b)中,若∠D=40°,∠B=30°,试求∠P的度数;
③猜想:∠P,∠B,∠D之间的数量关系为 .?
图15
答案
1.B
2.C [解析]
因为DE∥BC,所以∠C=∠AED=54°.因为∠A=62°,所以∠B=180°-∠A-∠C=64°.
故选C.
3.A [解析]
因为∠B=67°,∠C=33°,所以∠BAC=80°.因为AD是△ABC的角平分线,所以∠CAD=∠BAC=40°.故选A.
4.B [解析]
∵l1∥l2,∴∠1=∠CAB=70°.
∵BC⊥l3交l1于点B,∴∠ACB=90°,∴∠2=180°-90°-70°=20°.
5.A [解析]
由题意知∠E=45°,∠B=30°.
∵DE∥BC,∴∠BCF=∠E=45°.在△CFB中,∠BFC=180°-∠B-∠BCF=180°-30°-45°=105°.
6.D [解析]
∵∠A+∠B+∠C=180°,∠A=∠C-∠B,∴2∠C=180°,∴∠C=90°.
7.276
8.28° [解析]
∵△ABC的两条高AD,BE交于点F,∴∠AEF=∠BDF=90°.∵∠AFE=∠BFD,∴∠CAD=∠DBF=28°.
9.40 [解析]
∵BO平分∠ABC,CO平分∠ACB,∴∠OBC=∠ABC,∠OCB=∠ACB.∵∠BOC+∠OBC+∠OCB=180°,∴∠BOC=180°-(∠ABC+∠ACB).∵∠ABC+∠ACB=180°-∠A,∴∠BOC=90°+∠A.∵∠BOC=110°,∴90°+∠A=110°,∴∠A=40°.
10.[解析]
这是一道利用三角形内角和定理求各内角度数的计算题,由已知可知∠A,∠B,∠C三者之间存在着倍数关系,即∠B=∠C=2∠A,因此可以先求∠A,再求∠B,∠C.
解:因为∠A=∠B=∠C(已知),
所以∠B=∠C=2∠A(等式的性质).
因为∠A+∠B+∠C=180°(三角形内角和等于180°),
所以∠A+2∠A+2∠A=180°(等量代换),
所以∠A=36°,
所以∠B=2∠A=72°,∠C=2∠A=72°.
11.解:∵∠BDC=58°,∠C=92°,
∴∠DBC=180°-∠BDC-∠C=30°.
∵BD平分∠ABC,
∴∠ABC=2∠DBC=60°,
∴∠BAC=180°-∠ABC-∠C=180°-60°-92°=28°.
∵AP平分∠BAC,
∴∠BAP=∠BAC=×28°=14°.
12.解:因为∠B=∠C,∠A=56°,
所以∠B=∠C=62°.
因为FD⊥BC,DE⊥AB,
所以∠BED=∠BDF=90°.
所以∠BDE=180°-90°-∠B=28°.
所以∠EDF=∠BDF-∠BDE=90°-28°=62°.
13.B
14.α=β+γ [解析]
因为三角形内角和是一个定值,为180°,所以∠A+∠B+∠C=180°,
当∠A越来越小,∠B,∠C越来越大时,∠A-α+∠B+β+∠C+γ=180°,
所以α=β+γ.
故答案为α=β+γ.
15.110°
或50°
16.解:(1)∵∠C=60°,∠B=44°,
∴∠BAC=180°-60°-44°=76°.
∵AE平分∠BAC,
∴∠BAE=∠BAC=×76°=38°.
在Rt△ABD中,∠BAD=90°-44°=46°,
∴∠EAD=∠BAD-∠BAE=46°-38°=8°.
(2)∠EAD=(∠C-∠B).
理由:由(1)得∠EAD=∠BAD-∠BAE=90°-∠B-∠BAC①.
同理可得∠EAD=∠EAC-∠DAC=∠BAC-(90°-∠C)②.
①+②,得2∠EAD=∠C-∠B,
∴∠EAD=(∠C-∠B).
17.解:(1)∠A+∠D=∠C+∠B
(2)①6
②如图,根据“8字形”角的规律,可得∠1+∠D=∠3+∠P(Ⅰ),∠2+∠P=∠4+∠B(Ⅱ).
因为AP,CP分别平分∠DAB,∠BCD,
所以∠1=∠2,∠3=∠4.
(Ⅰ)-(Ⅱ),得2∠P=∠B+∠D,
所以∠P=(30°+40°)÷2=35°.
③∠P=(∠B+∠D)
【基础练习】
知识点
三角形内角和定理
1.如图1,在△ABC中,∠A=60°,∠B=40°,则∠C等于( )
图1
A.100°
B.80°
C.60°
D.40°
2.[教材随堂练习第3题变式]
如图2,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的度数为( )
图2
A.54°
B.62°
C.64°
D.74°
3.如图3,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为( )
图3
A.40°
B.45°
C.50°
D.55°
4.如图4,直线l1∥l2,直线l3与l1,l2分别交于点A,C,BC⊥l3交l1于点B.若∠1=70°,则∠2的度数为( )
图4
A.10°
B.20°
C.30°
D.40°
5.一副三角尺如图5所示摆放(直角顶点重合),边AB与CE交于点F,DE∥BC,则∠BFC等于( )
图5
A.105°
B.100°
C.75°
D.60°
6.在△ABC中,若一个内角等于另外两个内角的差,则( )
A.必有一个内角等于30°
B.必有一个内角等于45°
C.必有一个内角等于60°
D.必有一个内角等于90°
7.如图6,∠1+∠2+∠3+∠4= °.?
图6
8.如图7,△ABC的两条高AD,BE交于点F,∠DBF=28°,则∠CAD的度数为 .?
图7
图8
9.如图8,在△ABC中,BO,CO分别平分∠ABC,∠ACB.若∠BOC=110°,则∠A= °.?
10.在△ABC中,若∠A=∠B=∠C,求∠A,∠B,∠C的度数.
11.如图9,在△ABC中,∠C=92°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P,∠BDC=58°,求∠BAP的度数.
图9
12.如图10,在△ABC中,∠B=∠C,F为AC上一点,FD⊥BC于点D,DE⊥AB于点E,∠A=56°,求∠EDF的度数.
图10
【能力提升】
13.如图11,在△ABC中,∠B+∠C=100°,AD平分∠BAC交BC于点D,DE∥AB交AC于点E,则∠ADE的度数是( )
图11
A.30°
B.40°
C.50°
D.60°
14.如图12,在△ABC中,BC边不动,点A竖直向上运动,则∠A越来越小,∠B,∠C越来越大.若∠A减小α度,∠B增加β度,∠C增加γ度,则α,β,γ三者之间的等量关系是 .?
图12
15.如图13,在△ABC中,∠A=70°,∠B=50°,D,E分别为AB,AC上的点,沿DE折叠△ABC使点A落在BC边上的点F处.若△EFC为直角三角形,则∠BDF的度数为 .?
图13
16.如图14所示,在△ABC中,已知∠C>∠B,AD⊥BC于点D,AE平分∠BAC交BC于点E.
(1)若∠C=60°,∠B=44°,求∠EAD的度数;
(2)猜想∠EAD与(∠C-∠B)的关系,并说明理由.
图14
17.如图15(a),线段AB,CD相交于点O,连接AD,CB,我们把这样的图形称为“8字形”.
(1)请直接写出图(a)中∠A,∠B,∠C,∠D之间的数量关系: .?
(2)如图(b),在图(a)的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并分别与CD,AB相交于点M,N.
①图(b)中“8字形”有 个;?
②在图(b)中,若∠D=40°,∠B=30°,试求∠P的度数;
③猜想:∠P,∠B,∠D之间的数量关系为 .?
图15
答案
1.B
2.C [解析]
因为DE∥BC,所以∠C=∠AED=54°.因为∠A=62°,所以∠B=180°-∠A-∠C=64°.
故选C.
3.A [解析]
因为∠B=67°,∠C=33°,所以∠BAC=80°.因为AD是△ABC的角平分线,所以∠CAD=∠BAC=40°.故选A.
4.B [解析]
∵l1∥l2,∴∠1=∠CAB=70°.
∵BC⊥l3交l1于点B,∴∠ACB=90°,∴∠2=180°-90°-70°=20°.
5.A [解析]
由题意知∠E=45°,∠B=30°.
∵DE∥BC,∴∠BCF=∠E=45°.在△CFB中,∠BFC=180°-∠B-∠BCF=180°-30°-45°=105°.
6.D [解析]
∵∠A+∠B+∠C=180°,∠A=∠C-∠B,∴2∠C=180°,∴∠C=90°.
7.276
8.28° [解析]
∵△ABC的两条高AD,BE交于点F,∴∠AEF=∠BDF=90°.∵∠AFE=∠BFD,∴∠CAD=∠DBF=28°.
9.40 [解析]
∵BO平分∠ABC,CO平分∠ACB,∴∠OBC=∠ABC,∠OCB=∠ACB.∵∠BOC+∠OBC+∠OCB=180°,∴∠BOC=180°-(∠ABC+∠ACB).∵∠ABC+∠ACB=180°-∠A,∴∠BOC=90°+∠A.∵∠BOC=110°,∴90°+∠A=110°,∴∠A=40°.
10.[解析]
这是一道利用三角形内角和定理求各内角度数的计算题,由已知可知∠A,∠B,∠C三者之间存在着倍数关系,即∠B=∠C=2∠A,因此可以先求∠A,再求∠B,∠C.
解:因为∠A=∠B=∠C(已知),
所以∠B=∠C=2∠A(等式的性质).
因为∠A+∠B+∠C=180°(三角形内角和等于180°),
所以∠A+2∠A+2∠A=180°(等量代换),
所以∠A=36°,
所以∠B=2∠A=72°,∠C=2∠A=72°.
11.解:∵∠BDC=58°,∠C=92°,
∴∠DBC=180°-∠BDC-∠C=30°.
∵BD平分∠ABC,
∴∠ABC=2∠DBC=60°,
∴∠BAC=180°-∠ABC-∠C=180°-60°-92°=28°.
∵AP平分∠BAC,
∴∠BAP=∠BAC=×28°=14°.
12.解:因为∠B=∠C,∠A=56°,
所以∠B=∠C=62°.
因为FD⊥BC,DE⊥AB,
所以∠BED=∠BDF=90°.
所以∠BDE=180°-90°-∠B=28°.
所以∠EDF=∠BDF-∠BDE=90°-28°=62°.
13.B
14.α=β+γ [解析]
因为三角形内角和是一个定值,为180°,所以∠A+∠B+∠C=180°,
当∠A越来越小,∠B,∠C越来越大时,∠A-α+∠B+β+∠C+γ=180°,
所以α=β+γ.
故答案为α=β+γ.
15.110°
或50°
16.解:(1)∵∠C=60°,∠B=44°,
∴∠BAC=180°-60°-44°=76°.
∵AE平分∠BAC,
∴∠BAE=∠BAC=×76°=38°.
在Rt△ABD中,∠BAD=90°-44°=46°,
∴∠EAD=∠BAD-∠BAE=46°-38°=8°.
(2)∠EAD=(∠C-∠B).
理由:由(1)得∠EAD=∠BAD-∠BAE=90°-∠B-∠BAC①.
同理可得∠EAD=∠EAC-∠DAC=∠BAC-(90°-∠C)②.
①+②,得2∠EAD=∠C-∠B,
∴∠EAD=(∠C-∠B).
17.解:(1)∠A+∠D=∠C+∠B
(2)①6
②如图,根据“8字形”角的规律,可得∠1+∠D=∠3+∠P(Ⅰ),∠2+∠P=∠4+∠B(Ⅱ).
因为AP,CP分别平分∠DAB,∠BCD,
所以∠1=∠2,∠3=∠4.
(Ⅰ)-(Ⅱ),得2∠P=∠B+∠D,
所以∠P=(30°+40°)÷2=35°.
③∠P=(∠B+∠D)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
