第七章 平行线的证明 7.5 第2课时 三角形的外角练习题 2021-2022学年北师大版八年级数学上册(word版含答案)
文档属性
| 名称 | 第七章 平行线的证明 7.5 第2课时 三角形的外角练习题 2021-2022学年北师大版八年级数学上册(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 145.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 00:00:00 | ||
图片预览




文档简介
第2课时 三角形的外角
【基础练习】
知识点1
三角形的外角定理1
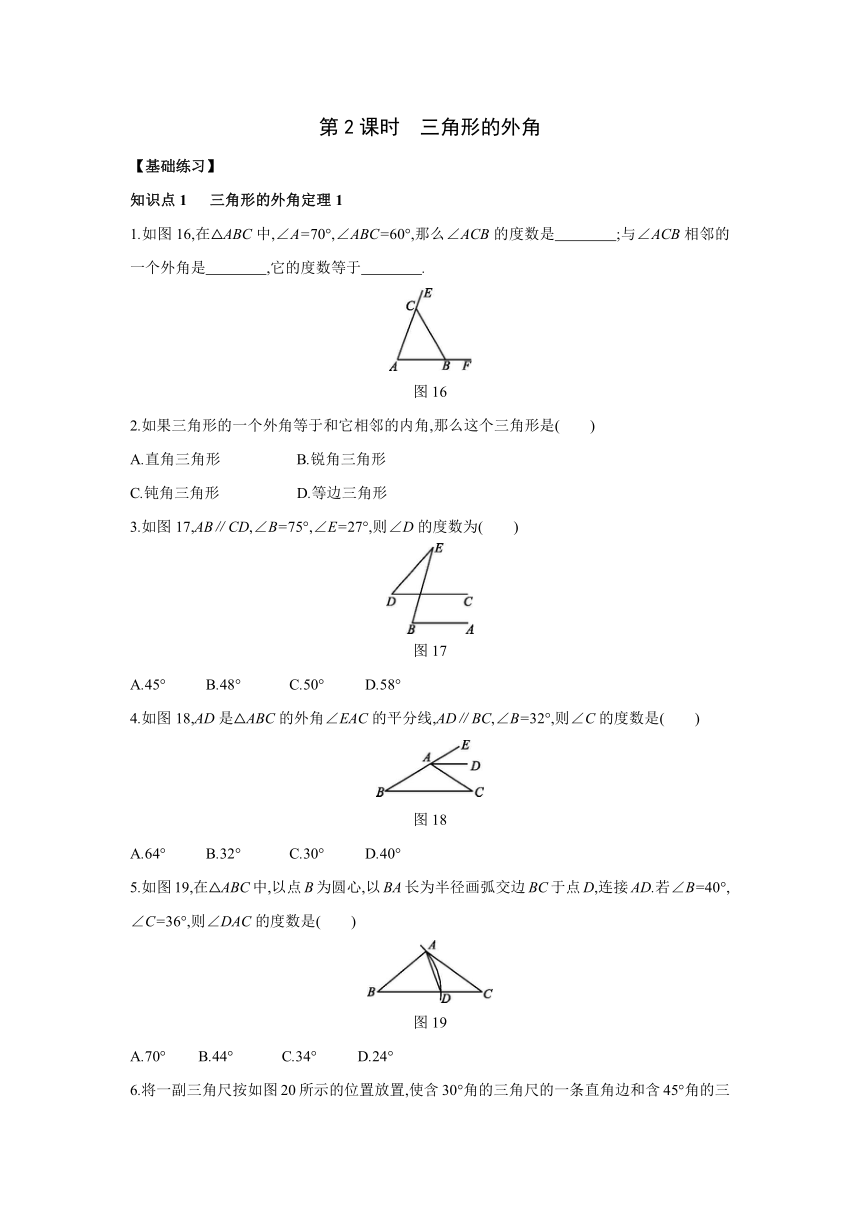
1.如图16,在△ABC中,∠A=70°,∠ABC=60°,那么∠ACB的度数是 ;与∠ACB相邻的一个外角是 ,它的度数等于 .?
图16
2.如果三角形的一个外角等于和它相邻的内角,那么这个三角形是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
3.如图17,AB∥CD,∠B=75°,∠E=27°,则∠D的度数为( )
图17
A.45°
B.48°
C.50°
D.58°
4.如图18,AD是△ABC的外角∠EAC的平分线,AD∥BC,∠B=32°,则∠C的度数是( )
图18
A.64°
B.32°
C.30°
D.40°
5.如图19,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的度数是( )
图19
A.70°
B.44°
C.34°
D.24°
6.将一副三角尺按如图20所示的位置放置,使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边放在同一条直线上,则∠α的度数是( )
图20
A.45°
B.60°
C.75°
D.85°
7.如图21,D是△ABC的边AC上一点,E是BD上一点,连接EC,若∠A=60°,∠ABD=25°,∠DCE=35°,求∠BEC的度数.
图21
8.一个零件的形状如图22所示,按规定∠A应等于90°,∠B,∠C应分别是21°和32°,现测量得∠BDC=148°,你认为这个零件合格吗?为什么?
图22
知识点2
三角形的外角定理2
9.如图23,下列说法中错误的是( )
图23
A.∠1不是△ABC的外角
B.∠ACD是△ABC的外角
C.∠ACD>∠A+∠B
D.∠B<∠1+∠2
10.如图24,P是△ABC内一点,连接BP并延长交AC于点D,连接PC,则图中∠1,∠2,∠A的大小关系是( )
图24
A.∠A>∠2>∠1
B.∠A>∠1>∠2
C.∠2>∠1>∠A
D
∠1>∠2>∠A
11.如图25,已知CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E.
求证:∠BAC>∠B.
图25
【能力提升】
12.如图26,在△CEF中,∠E=80°,∠F=50°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是
( )
图26
A.45°
B.50°
C.55°
D.80°
13.如图27所示,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG∥CE,交AB于点G,则下列说法正确的是( )
图27
A.∠2+∠3>∠1
B.∠2+∠3<∠1
C.∠2+∠3=∠1
D.以上均不对
14.如图28所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.
图28
15.如图29所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,E是AD上一点,连接BE.
求证:∠BED>∠C.
图29
16.已知:如图30,在△ABC中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM平分∠ABC,E为射线BM上一点.
(1)连接CE.
①若CE∥AB,求∠BEC的度数;
②若CE平分∠ACD,求∠BEC的度数.
(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.
图30
答案
1.50° ∠BCE 130° [解析]
由三角形内角和定理,得∠ACB=180°-70°-60°=50°,则∠BCE=180°-∠ACB=130°.
2.A [解析]
三角形的一个外角与和它相邻的内角的度数和为180°.又因为三角形的一个外角等于和它相邻的内角,所以三角形的这个内角为90°,即这个三角形是直角三角形.
3.B 4.B 5.C 6.C
7.解:∵∠BDC是△ABD的外角,
∴∠BDC=∠A+∠ABD=60°+25°=85°.
同理∠BEC=∠BDC+∠DCE=85°+35°=120°.
8.解:不合格.理由:如图,延长CD与AB相交于点F.
若此零件合格,则∠DFB=∠C+∠A=32°+90°=122°,∠BDC=∠DFB+∠B=122°+21°=143°.
因为实际量得的∠BDC=148°,143°≠148°,
所以这个零件不合格.
9.C 10.D
11.证明:∵CE是∠ACD的平分线,∴∠ACE=∠ECD.∵∠ECD是△BEC的外角,
∴∠ECD>∠B.∵∠BAC是△AEC的外角,∴∠BAC>∠ACE,∴∠BAC>∠ECD,
∴∠BAC>∠B.
12.B [解析]
在△CEF中,∵∠E=80°,∠F=50°,∴∠ECF=50°.
如图,延长BC交AD于点M.
∵AB∥CF,AD∥CE,
∴∠B=∠BCF,∠BMD=∠BCE=50°+∠BCF.
又∵∠BMD=∠A+∠B,∴∠A=50°.
13.C
14.解:设∠1=∠2=x,则∠3=∠4=2x.
因为∠BAC=63°,
所以∠2+∠4=117°,即x+2x=117°.
所以x=39°.所以∠1=39°,
所以∠DAC=∠BAC-∠1=63°-39°=24°.
15.[解析]
要证明一个角大于另一个角,可用三角形的一个外角大于任何一个和它不相邻的内角,但显然∠BED与∠C之间并不存在外角和内角的关系,所以一定存在一个“中间量”,这个中间量起着桥梁的作用:∠BED>∠BAD=∠C.这种策略是证明角之间不等关系的常用方法.
证明:因为∠BAC=90°,
所以∠BAD+∠CAD=90°.
因为AD⊥BC,
所以∠ADC=90°.
所以∠C+∠CAD=180°-90°=90°.
所以∠BAD=∠C.
因为∠BED是△BAE的外角,
所以∠BED>∠BAD(三角形的一个外角大于任何一个和它不相邻的内角).
所以∠BED>∠C.
[点评]
证明两个角的大小关系,一般用到三角形外角与内角之间的关系,这是解题的突破口,但它们之间往往没有直接的联系,这时需要找中间量“过渡”或作辅助线“架桥”,这是解题的关键.
16.解:(1)①因为∠A=60°,∠ACB=40°,
所以∠ABC=80°.
因为BM平分∠ABC,
所以∠ABE=∠ABC=40°.
因为CE∥AB,所以∠BEC=∠ABE=40°.
②因为∠A=60°,∠ACB=40°,
所以∠ABC=80°,
∠ACD=180°-∠ACB=180°-40°=140°.
因为BM平分∠ABC,CE平分∠ACD,
所以∠CBE=∠ABC=40°,
∠ECD=∠ACD=70°.
所以∠BEC=∠ECD-∠CBE=70°-40°=30°.
(2)①若CE⊥BC,则∠ECD=90°.
因为∠CBE=40°,所以∠BEC=50°;
②若CE⊥AB,
因为∠ABE=40°,
所以∠BEC=90°+40°=130°;
③若CE⊥AC,
因为∠CBE=40°,∠ACB=40°,
所以∠BEC=180°-40°-40°-90°=10°.
综上所述,∠BEC的度数为50°或130°或10°.
【基础练习】
知识点1
三角形的外角定理1
1.如图16,在△ABC中,∠A=70°,∠ABC=60°,那么∠ACB的度数是 ;与∠ACB相邻的一个外角是 ,它的度数等于 .?
图16
2.如果三角形的一个外角等于和它相邻的内角,那么这个三角形是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
3.如图17,AB∥CD,∠B=75°,∠E=27°,则∠D的度数为( )
图17
A.45°
B.48°
C.50°
D.58°
4.如图18,AD是△ABC的外角∠EAC的平分线,AD∥BC,∠B=32°,则∠C的度数是( )
图18
A.64°
B.32°
C.30°
D.40°
5.如图19,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的度数是( )
图19
A.70°
B.44°
C.34°
D.24°
6.将一副三角尺按如图20所示的位置放置,使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边放在同一条直线上,则∠α的度数是( )
图20
A.45°
B.60°
C.75°
D.85°
7.如图21,D是△ABC的边AC上一点,E是BD上一点,连接EC,若∠A=60°,∠ABD=25°,∠DCE=35°,求∠BEC的度数.
图21
8.一个零件的形状如图22所示,按规定∠A应等于90°,∠B,∠C应分别是21°和32°,现测量得∠BDC=148°,你认为这个零件合格吗?为什么?
图22
知识点2
三角形的外角定理2
9.如图23,下列说法中错误的是( )
图23
A.∠1不是△ABC的外角
B.∠ACD是△ABC的外角
C.∠ACD>∠A+∠B
D.∠B<∠1+∠2
10.如图24,P是△ABC内一点,连接BP并延长交AC于点D,连接PC,则图中∠1,∠2,∠A的大小关系是( )
图24
A.∠A>∠2>∠1
B.∠A>∠1>∠2
C.∠2>∠1>∠A
D
∠1>∠2>∠A
11.如图25,已知CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E.
求证:∠BAC>∠B.
图25
【能力提升】
12.如图26,在△CEF中,∠E=80°,∠F=50°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是
( )
图26
A.45°
B.50°
C.55°
D.80°
13.如图27所示,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG∥CE,交AB于点G,则下列说法正确的是( )
图27
A.∠2+∠3>∠1
B.∠2+∠3<∠1
C.∠2+∠3=∠1
D.以上均不对
14.如图28所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.
图28
15.如图29所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,E是AD上一点,连接BE.
求证:∠BED>∠C.
图29
16.已知:如图30,在△ABC中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM平分∠ABC,E为射线BM上一点.
(1)连接CE.
①若CE∥AB,求∠BEC的度数;
②若CE平分∠ACD,求∠BEC的度数.
(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.
图30
答案
1.50° ∠BCE 130° [解析]
由三角形内角和定理,得∠ACB=180°-70°-60°=50°,则∠BCE=180°-∠ACB=130°.
2.A [解析]
三角形的一个外角与和它相邻的内角的度数和为180°.又因为三角形的一个外角等于和它相邻的内角,所以三角形的这个内角为90°,即这个三角形是直角三角形.
3.B 4.B 5.C 6.C
7.解:∵∠BDC是△ABD的外角,
∴∠BDC=∠A+∠ABD=60°+25°=85°.
同理∠BEC=∠BDC+∠DCE=85°+35°=120°.
8.解:不合格.理由:如图,延长CD与AB相交于点F.
若此零件合格,则∠DFB=∠C+∠A=32°+90°=122°,∠BDC=∠DFB+∠B=122°+21°=143°.
因为实际量得的∠BDC=148°,143°≠148°,
所以这个零件不合格.
9.C 10.D
11.证明:∵CE是∠ACD的平分线,∴∠ACE=∠ECD.∵∠ECD是△BEC的外角,
∴∠ECD>∠B.∵∠BAC是△AEC的外角,∴∠BAC>∠ACE,∴∠BAC>∠ECD,
∴∠BAC>∠B.
12.B [解析]
在△CEF中,∵∠E=80°,∠F=50°,∴∠ECF=50°.
如图,延长BC交AD于点M.
∵AB∥CF,AD∥CE,
∴∠B=∠BCF,∠BMD=∠BCE=50°+∠BCF.
又∵∠BMD=∠A+∠B,∴∠A=50°.
13.C
14.解:设∠1=∠2=x,则∠3=∠4=2x.
因为∠BAC=63°,
所以∠2+∠4=117°,即x+2x=117°.
所以x=39°.所以∠1=39°,
所以∠DAC=∠BAC-∠1=63°-39°=24°.
15.[解析]
要证明一个角大于另一个角,可用三角形的一个外角大于任何一个和它不相邻的内角,但显然∠BED与∠C之间并不存在外角和内角的关系,所以一定存在一个“中间量”,这个中间量起着桥梁的作用:∠BED>∠BAD=∠C.这种策略是证明角之间不等关系的常用方法.
证明:因为∠BAC=90°,
所以∠BAD+∠CAD=90°.
因为AD⊥BC,
所以∠ADC=90°.
所以∠C+∠CAD=180°-90°=90°.
所以∠BAD=∠C.
因为∠BED是△BAE的外角,
所以∠BED>∠BAD(三角形的一个外角大于任何一个和它不相邻的内角).
所以∠BED>∠C.
[点评]
证明两个角的大小关系,一般用到三角形外角与内角之间的关系,这是解题的突破口,但它们之间往往没有直接的联系,这时需要找中间量“过渡”或作辅助线“架桥”,这是解题的关键.
16.解:(1)①因为∠A=60°,∠ACB=40°,
所以∠ABC=80°.
因为BM平分∠ABC,
所以∠ABE=∠ABC=40°.
因为CE∥AB,所以∠BEC=∠ABE=40°.
②因为∠A=60°,∠ACB=40°,
所以∠ABC=80°,
∠ACD=180°-∠ACB=180°-40°=140°.
因为BM平分∠ABC,CE平分∠ACD,
所以∠CBE=∠ABC=40°,
∠ECD=∠ACD=70°.
所以∠BEC=∠ECD-∠CBE=70°-40°=30°.
(2)①若CE⊥BC,则∠ECD=90°.
因为∠CBE=40°,所以∠BEC=50°;
②若CE⊥AB,
因为∠ABE=40°,
所以∠BEC=90°+40°=130°;
③若CE⊥AC,
因为∠CBE=40°,∠ACB=40°,
所以∠BEC=180°-40°-40°-90°=10°.
综上所述,∠BEC的度数为50°或130°或10°.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
