第二十六章综合运用数学知识解决实际问题单元测试题 2020——2021学年京改版九年级数学下册(Word版含答案)
文档属性
| 名称 | 第二十六章综合运用数学知识解决实际问题单元测试题 2020——2021学年京改版九年级数学下册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 178.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 17:01:27 | ||
图片预览


文档简介
第二十六章 综合运用数学知识解决实际问题
一、选择题(每题6分,共30分)
1.某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图1所示,在地面上取一点C,使C到A,B两点的距离均可测量,测量找到AC和BC的中点D,E,测得DE的长为1100
m,则隧道AB的长度为
( )
图1
A.3300
m
B.2200
m
C.1100
m
D.550
m
2.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图2.当小明把100个纸杯整齐地叠放在一起时,它们的高度约是
( )
图2
A.106
cm
B.110
cm
C.114
cm
D.116
cm
3.油电混动汽车是一种节油、环保的新技术汽车.它将行驶过程中部分原本被浪费的能量回收储存于内置的蓄电池中.汽车在低速行驶时,使用蓄电池带动电动机驱动汽车,节约燃油.某品牌油电混动汽车与普通汽车的相关成本数据估算如下表:
油电混动汽车
普通汽车
购买价格(万元)
17.48
15.98
每百千米燃油成本(元)
31
46
某人计划购入一辆上述品牌的汽车.他估算了未来10年的用车成本,在只考虑车价和燃油成本的情况下,发现选择油电混动汽车的成本不高于选择普通汽车的成本.则他在估算时,预计平均每年行驶的千米数至少为
( )
A.5000千米
B.10000千米
C.15000千米
D.20000
千米
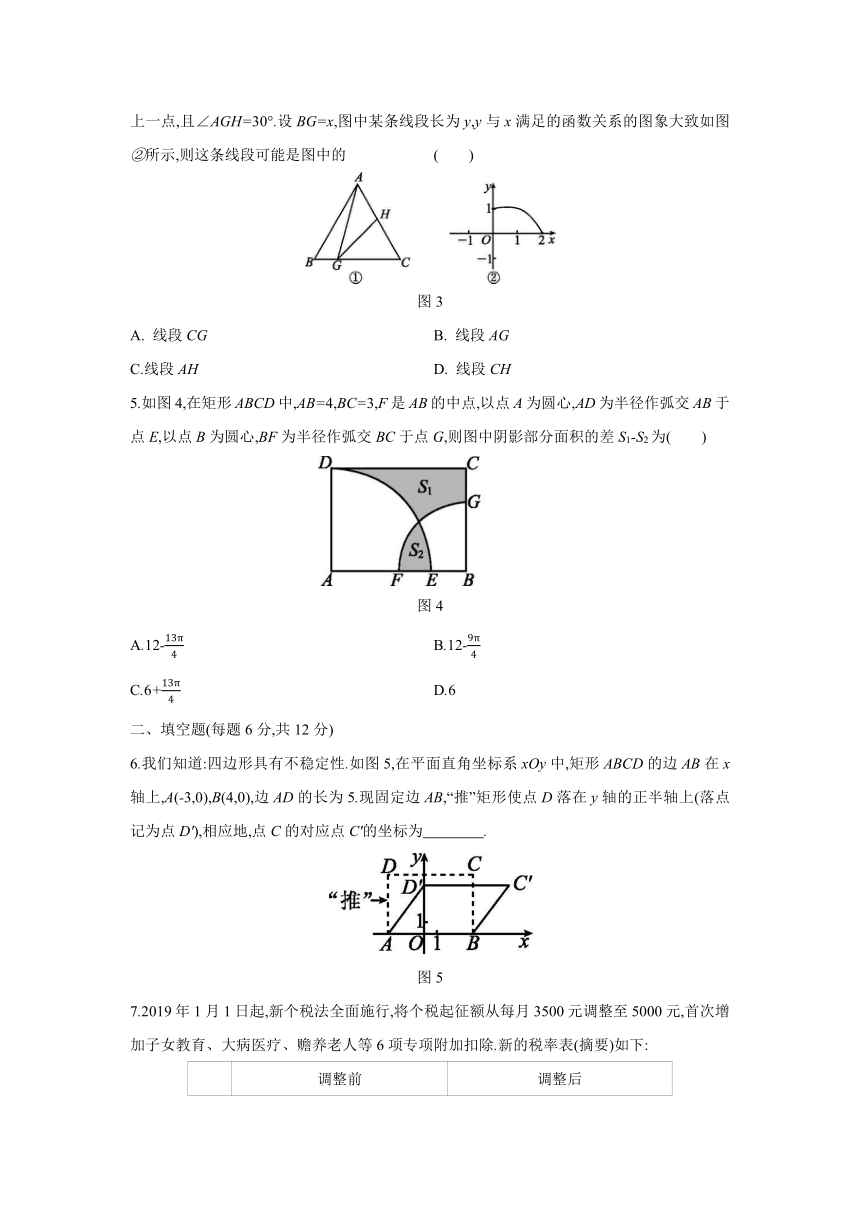
4.如图3①,在等边三角形ABC中,AB=2,G是BC边上一个动点且不与点B,C重合,H是AC边上一点,且∠AGH=30°.设BG=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图②所示,则这条线段可能是图中的
( )
图3
A.
线段CG
B.
线段AG
C.线段AH
D.
线段CH
5.如图4,在矩形ABCD中,AB=4,BC=3,F是AB的中点,以点A为圆心,AD为半径作弧交AB于点E,以点B为圆心,BF为半径作弧交BC于点G,则图中阴影部分面积的差S1-S2为( )
图4
A.12-
B.12-
C.6+
D.6
二、填空题(每题6分,共12分)
6.我们知道:四边形具有不稳定性.如图5,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,A(-3,0),B(4,0),边AD的长为5.现固定边AB,“推”矩形使点D落在y轴的正半轴上(落点记为点D'),相应地,点C的对应点C'的坐标为 .?
图5
7.2019年1月1日起,新个税法全面施行,将个税起征额从每月3500元调整至5000元,首次增加子女教育、大病医疗、赡养老人等6项专项附加扣除.新的税率表(摘要)如下:
调整前
调整后
分级
应纳税额
税率
应纳税额
税率
1
不超过1500元的
部分
3%
不超过3000元的部分
3%
2
超过1500元至4500元的部分
10%
超过3000元至12000元的部分
10%
(注:应纳税额=纳税所得额-起征额-专项附加扣除)
小吴2019年1月纳税所得额是7800元,专项附加扣除2000元,则小吴本月应缴税款 元;与此次个税调整前相比,他少缴税款 元.?
三、解答题(共58分)
8.(13分)如图6,在一次对某海岛巡航过程中,巡航飞机的飞行高度为2001米,在点A测得岛上山峰顶点F的俯角为30°,保持方向不变前进1200米到达点B后测得点F的俯角为45°.请据此计算该海岛的最高海拔是多少米.(结果精确到1米)
图6
9.(15分)在某市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板.经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元;
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有哪几种购买方案,哪种方案费用最低.
10.(15分)在重阳节敬老爱老活动中,某校计划组织志愿者服务小组到“夕阳红”敬老院为老人服务,准备从九年级(1)班中的3名男生小亮、小明、小伟和2名女生小丽、小敏中随机选取一名男生和一名女生参加学校志愿者服务小组.
(1)请用画树状图法或列表法写出所有可能出现的结果;
(2)求出恰好选中男生小明与女生小丽的概率.
11.(15分)在“美丽广西,清洁乡村”活动中,李家村村主任提出了两种购买垃圾桶的方案.方案一:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用为250元;方案二:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用为500元.设方案一的购买费和每月垃圾处理费共为y1元,交费时间为x个月;方案二的购买费和每月垃圾处理费共为y2元,交费时间为x个月.
(1)直接写出y1,y2与x之间的函数表达式(不要求写自变量的取值范围);
(2)在如图7所示的平面直角坐标系内,分别画出函数y1,y2的图象;
(3)在垃圾桶使用寿命相同的情况下,哪种方案省钱?
图7
答案
1.B 2.A
3.B [解析]
设平均每年行驶的千米数为x千米,根据题意,得174800+≤159800+,
解得x≥10000.即平均每年行驶的千米数至少为10000千米.
4.D 5.A 6.(7,4)
7.24 301 [解析]
根据调整后应纳税额=纳税所得额-起征额-专项附加扣除,小吴2019年1月应纳税额为7800-5000-2000=800(元),
∴小吴本月应缴税款:800×3%=24(元).
按调整前来计算应纳税额为7800-3500=4300(元),
应纳税款为1500×3%+(4300-1500)×10%=325(元),
故与此次个税调整前相比,他少缴税款301元.
8.解:过点F作FC⊥AB,交AB的延长线于点C.设CF=x米.
在Rt△ACF和Rt△BCF中,
∵∠BAF=30°,∠CBF=45°,
∴BC=CF=x米,=tan30°,
即AC=x米.
∵AC-BC=AB=1200米,
∴x-x=1200,
解得x=600(+1),
则DF=h-x=2001-600(+1)≈362(米).
答:该海岛的最高海拔约是362米.
9.解:(1)设每台电脑x万元,每台电子白板y万元.
根据题意,得
解得
答:每台电脑0.5万元,每台电子白板1.5万元.
(2)设购进电脑a台,则购进电子白板(30-a)台.
根据题意,得
解得15≤a≤17,即a的值为15,16,17.
故共有三种方案.
方案一:购进电脑15台,电子白板15台.总费用为0.5×15+1.5×15=30(万元);
方案二:购进电脑16台,电子白板14台.总费用为0.5×16+1.5×14=29(万元);
方案三:购进电脑17台,电子白板13台.总费用为0.5×17+1.5×13=28(万元).
因为28<29<30,所以方案三费用最低.
10.解:(1)列表如下:
小亮
小明
小伟
小丽
小丽,小亮
小丽,小明
小丽,小伟
小敏
小敏,小亮
小敏,小明
小敏,小伟
(2)由(1),得共有6种等可能的情况,而正好选中男生小明与女生小丽的有1种情况,
∴P(恰好选中男生小明与女生小丽)=.
11.解:(1)由题意,得y1=250x+3000,y2=500x+1000.
(2)如图所示.
(3)由图象可知:①当使用时间大于8个月时,直线y1落在直线y2的下方,y1②当使用时间小于8个月时,直线y2落在直线y1的下方,y2③当使用时间等于8个月时,y1=y2,即方案一与方案二花费相同.
一、选择题(每题6分,共30分)
1.某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图1所示,在地面上取一点C,使C到A,B两点的距离均可测量,测量找到AC和BC的中点D,E,测得DE的长为1100
m,则隧道AB的长度为
( )
图1
A.3300
m
B.2200
m
C.1100
m
D.550
m
2.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图2.当小明把100个纸杯整齐地叠放在一起时,它们的高度约是
( )
图2
A.106
cm
B.110
cm
C.114
cm
D.116
cm
3.油电混动汽车是一种节油、环保的新技术汽车.它将行驶过程中部分原本被浪费的能量回收储存于内置的蓄电池中.汽车在低速行驶时,使用蓄电池带动电动机驱动汽车,节约燃油.某品牌油电混动汽车与普通汽车的相关成本数据估算如下表:
油电混动汽车
普通汽车
购买价格(万元)
17.48
15.98
每百千米燃油成本(元)
31
46
某人计划购入一辆上述品牌的汽车.他估算了未来10年的用车成本,在只考虑车价和燃油成本的情况下,发现选择油电混动汽车的成本不高于选择普通汽车的成本.则他在估算时,预计平均每年行驶的千米数至少为
( )
A.5000千米
B.10000千米
C.15000千米
D.20000
千米
4.如图3①,在等边三角形ABC中,AB=2,G是BC边上一个动点且不与点B,C重合,H是AC边上一点,且∠AGH=30°.设BG=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图②所示,则这条线段可能是图中的
( )
图3
A.
线段CG
B.
线段AG
C.线段AH
D.
线段CH
5.如图4,在矩形ABCD中,AB=4,BC=3,F是AB的中点,以点A为圆心,AD为半径作弧交AB于点E,以点B为圆心,BF为半径作弧交BC于点G,则图中阴影部分面积的差S1-S2为( )
图4
A.12-
B.12-
C.6+
D.6
二、填空题(每题6分,共12分)
6.我们知道:四边形具有不稳定性.如图5,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,A(-3,0),B(4,0),边AD的长为5.现固定边AB,“推”矩形使点D落在y轴的正半轴上(落点记为点D'),相应地,点C的对应点C'的坐标为 .?
图5
7.2019年1月1日起,新个税法全面施行,将个税起征额从每月3500元调整至5000元,首次增加子女教育、大病医疗、赡养老人等6项专项附加扣除.新的税率表(摘要)如下:
调整前
调整后
分级
应纳税额
税率
应纳税额
税率
1
不超过1500元的
部分
3%
不超过3000元的部分
3%
2
超过1500元至4500元的部分
10%
超过3000元至12000元的部分
10%
(注:应纳税额=纳税所得额-起征额-专项附加扣除)
小吴2019年1月纳税所得额是7800元,专项附加扣除2000元,则小吴本月应缴税款 元;与此次个税调整前相比,他少缴税款 元.?
三、解答题(共58分)
8.(13分)如图6,在一次对某海岛巡航过程中,巡航飞机的飞行高度为2001米,在点A测得岛上山峰顶点F的俯角为30°,保持方向不变前进1200米到达点B后测得点F的俯角为45°.请据此计算该海岛的最高海拔是多少米.(结果精确到1米)
图6
9.(15分)在某市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板.经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元;
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有哪几种购买方案,哪种方案费用最低.
10.(15分)在重阳节敬老爱老活动中,某校计划组织志愿者服务小组到“夕阳红”敬老院为老人服务,准备从九年级(1)班中的3名男生小亮、小明、小伟和2名女生小丽、小敏中随机选取一名男生和一名女生参加学校志愿者服务小组.
(1)请用画树状图法或列表法写出所有可能出现的结果;
(2)求出恰好选中男生小明与女生小丽的概率.
11.(15分)在“美丽广西,清洁乡村”活动中,李家村村主任提出了两种购买垃圾桶的方案.方案一:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用为250元;方案二:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用为500元.设方案一的购买费和每月垃圾处理费共为y1元,交费时间为x个月;方案二的购买费和每月垃圾处理费共为y2元,交费时间为x个月.
(1)直接写出y1,y2与x之间的函数表达式(不要求写自变量的取值范围);
(2)在如图7所示的平面直角坐标系内,分别画出函数y1,y2的图象;
(3)在垃圾桶使用寿命相同的情况下,哪种方案省钱?
图7
答案
1.B 2.A
3.B [解析]
设平均每年行驶的千米数为x千米,根据题意,得174800+≤159800+,
解得x≥10000.即平均每年行驶的千米数至少为10000千米.
4.D 5.A 6.(7,4)
7.24 301 [解析]
根据调整后应纳税额=纳税所得额-起征额-专项附加扣除,小吴2019年1月应纳税额为7800-5000-2000=800(元),
∴小吴本月应缴税款:800×3%=24(元).
按调整前来计算应纳税额为7800-3500=4300(元),
应纳税款为1500×3%+(4300-1500)×10%=325(元),
故与此次个税调整前相比,他少缴税款301元.
8.解:过点F作FC⊥AB,交AB的延长线于点C.设CF=x米.
在Rt△ACF和Rt△BCF中,
∵∠BAF=30°,∠CBF=45°,
∴BC=CF=x米,=tan30°,
即AC=x米.
∵AC-BC=AB=1200米,
∴x-x=1200,
解得x=600(+1),
则DF=h-x=2001-600(+1)≈362(米).
答:该海岛的最高海拔约是362米.
9.解:(1)设每台电脑x万元,每台电子白板y万元.
根据题意,得
解得
答:每台电脑0.5万元,每台电子白板1.5万元.
(2)设购进电脑a台,则购进电子白板(30-a)台.
根据题意,得
解得15≤a≤17,即a的值为15,16,17.
故共有三种方案.
方案一:购进电脑15台,电子白板15台.总费用为0.5×15+1.5×15=30(万元);
方案二:购进电脑16台,电子白板14台.总费用为0.5×16+1.5×14=29(万元);
方案三:购进电脑17台,电子白板13台.总费用为0.5×17+1.5×13=28(万元).
因为28<29<30,所以方案三费用最低.
10.解:(1)列表如下:
小亮
小明
小伟
小丽
小丽,小亮
小丽,小明
小丽,小伟
小敏
小敏,小亮
小敏,小明
小敏,小伟
(2)由(1),得共有6种等可能的情况,而正好选中男生小明与女生小丽的有1种情况,
∴P(恰好选中男生小明与女生小丽)=.
11.解:(1)由题意,得y1=250x+3000,y2=500x+1000.
(2)如图所示.
(3)由图象可知:①当使用时间大于8个月时,直线y1落在直线y2的下方,y1
