第二十五章概率的求法与应用练习题 2020——2021学年京改版九年级数学下册(Word版含答案)
文档属性
| 名称 | 第二十五章概率的求法与应用练习题 2020——2021学年京改版九年级数学下册(Word版含答案) | 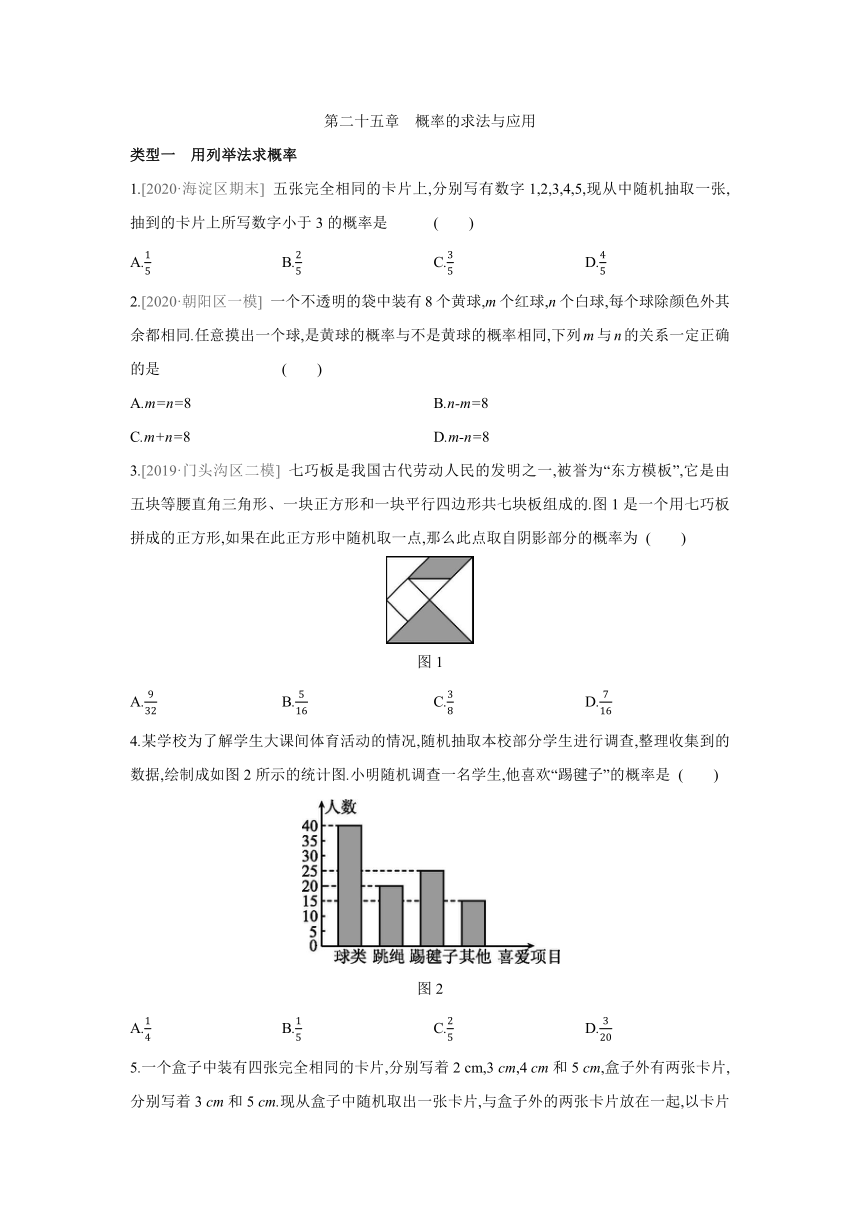 | |
| 格式 | docx | ||
| 文件大小 | 150.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 17:01:00 | ||
图片预览



文档简介
第二十五章 概率的求法与应用
类型一 用列举法求概率
1.[2020·海淀区期末]
五张完全相同的卡片上,分别写有数字1,2,3,4,5,现从中随机抽取一张,抽到的卡片上所写数字小于3的概率是
( )
A.
B.
C.
D.
2.[2020·朝阳区一模]
一个不透明的袋中装有8个黄球,m个红球,n个白球,每个球除颜色外其余都相同.任意摸出一个球,是黄球的概率与不是黄球的概率相同,下列m与n的关系一定正确的是
( )
A.m=n=8
B.n-m=8
C.m+n=8
D.m-n=8
3.[2019·门头沟区二模]
七巧板是我国古代劳动人民的发明之一,被誉为“东方模板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.图1是一个用七巧板拼成的正方形,如果在此正方形中随机取一点,那么此点取自阴影部分的概率为
( )
图1
A.
B.
C.
D.
4.某学校为了解学生大课间体育活动的情况,随机抽取本校部分学生进行调查,整理收集到的数据,绘制成如图2所示的统计图.小明随机调查一名学生,他喜欢“踢毽子”的概率是
( )
图2
A.
B.
C.
D.
5.一个盒子中装有四张完全相同的卡片,分别写着2
cm,3
cm,4
cm和5
cm,盒子外有两张卡片,分别写着3
cm和5
cm.现从盒子中随机取出一张卡片,与盒子外的两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,那么这三条线段能构成三角形的概率是
( )
A.
B.
C.
D.
类型二 用列表法、画树状图法求概率
6.在一个不透明的袋子里装有两个红球和两个黄球,它们除颜色不同外其余都相同.从中随机摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,两次都摸到黄球的概率是
( )
A.
B.
C.
D.
7.[2020·海淀区模拟]
从2020年5月1日起,北京正式施行“垃圾分类”,如图3是生活中的四个不同的垃圾分类投放桶.小明投放了两袋垃圾,不同类的概率是
( )
图3
A.
B.
C.
D.
类型三 概率与游戏公平性
8.现有A,B两个不透明的袋子,分别装有3个除颜色外其余完全相同的小球,其中A袋中装有2个白球,1个红球;B袋中装有2个红球,1个白球.小林和小华商定了一个游戏规则:从摇匀后的A,B两袋中各随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画树状图法,说明这个游戏对双方是否公平.
类型四 用频率估计概率
9.[2020·密云区二模]
新冠疫情发生以来,为保证防控期间的口罩供应,某公司加紧转产,开设多条生产线争分夺秒赶制口罩,从最初转产时的陌生,到正式投产后达成日均生产100万个口罩的产能.不仅效率高,而且口罩送检合格率也不断提升,真正体现了“大国速度”.以下是质监局对一批口罩进行质量抽检的相关数据,统计如下:
抽检数量n/个
20
50
100
200
500
1000
2000
5000
10000
合格数量m/个
19
46
93
185
459
922
1840
4595
9213
口罩合格率
0.950
0.920
0.930
0.925
0.918
0.922
0.920
0.919
0.921
下面四个推断合理的是
( )
A.当抽检口罩的数量是10000个时,口罩合格的数量是9213个,所以这批口罩中“口罩合格”的概率是0.921
B.由于抽检口罩的数量分别是50个和2000个时,口罩合格率均是0.920,所以可以估计这批口罩中“口罩合格”的概率是0.920
C.随着抽检数量的增加,“口罩合格”的频率总在0.920附近摆动,显示出一定的稳定性,所以可以估计这批口罩中“口罩合格”的概率是0.920
D.当抽检口罩的数量达到20000个时,“口罩合格”的概率一定是0.921
类型五 概率在实际生活中的应用
10.有两把不同的锁和三把钥匙,其中两把钥匙能打开同一把锁,第三把钥匙能打开另一把锁.任意取出一把钥匙去开任意的一把锁,一次能打开锁的概率是 .?
11.为了备战九年级物理、化学实验操作考试,某校对九年级学生进行了模拟训练.物理、化学各有4个不同的操作实验题目,物理用号码①,②,③,④代表,化学用字母a,b,c,d代表.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.
(1)请用画树状图法或列表法表示某个同学抽签的各种可能情况;
(2)小张同学对物理的①,②和化学的b,c号实验准备得较好,他同时抽到两科都准备得较好的实验题目的概率是多少?
类型六 概率与其他知识的综合应用
12.如图4,电路图上有四个开关A,B,C,D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光.
(1)任意闭合其中一个开关,则小灯泡发光的概率为 ;?
(2)任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.
图4
类型七 数学活动
13.在一个口袋中有4个完全相同的小球,把它们分别标上数字-1,0,1,2,随机地摸出一个小球记录数字,然后放回,再随机地摸出一个小球记录数字.求下列事件发生的概率:
(1)两次摸到的小球上的数字都是正数的概率P(A);
(2)两次摸到的小球上的数字和等于0的概率P(B).
答案
1.B 2.C 3.C 4.A
5.D 6.C 7.D
8.解:列表如下:
B
A
红1
红2
白
白1
(白1,红1)
(白1,红2)
(白1,白)
白2
(白2,红1)
(白2,红2)
(白2,白)
红
(红,红1)
(红,红2)
(红,白)
由上表可知,一共有9种等可能的结果,其中颜色相同的结果有4种,颜色不同的结果有5种.
∴P(颜色相同)=,P(颜色不同)=.
∵<,∴这个游戏对双方不公平.
9.C 10.
11.解:(1)画树状图如下:
或列表如下:
化学
物理
a
b
c
d
①
(①,a)
(①,b)
(①,c)
(①,d)
②
(②,a)
(②,b)
(②,c)
(②,d)
③
(③,a)
(③,b)
(③,c)
(③,d)
④
(④,a)
(④,b)
(④,c)
(④,d)
(2)由(1)可得所有等可能的情况共有16种,小张同学同时抽到两科都准备得较好的实验题目[即(①,b),(②,b),(①,c),(②,c)]的概率P==.
12.解:(1)
(2)画出树状图如下:
任意闭合其中两个开关的等可能的情况共有12种,其中能使小灯泡发光的情况有6种,所以P(小灯泡发光)==.
13.解:(1)画树状图如下:
所有可能出现的等可能结果共有16种,两个数字都是正数的结果有4种,所以P(A)==.
(2)由(1),得所有可能出现的等可能结果共有16种,其中两次的数字和为0的结果有3种,所以P(B)=.
类型一 用列举法求概率
1.[2020·海淀区期末]
五张完全相同的卡片上,分别写有数字1,2,3,4,5,现从中随机抽取一张,抽到的卡片上所写数字小于3的概率是
( )
A.
B.
C.
D.
2.[2020·朝阳区一模]
一个不透明的袋中装有8个黄球,m个红球,n个白球,每个球除颜色外其余都相同.任意摸出一个球,是黄球的概率与不是黄球的概率相同,下列m与n的关系一定正确的是
( )
A.m=n=8
B.n-m=8
C.m+n=8
D.m-n=8
3.[2019·门头沟区二模]
七巧板是我国古代劳动人民的发明之一,被誉为“东方模板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.图1是一个用七巧板拼成的正方形,如果在此正方形中随机取一点,那么此点取自阴影部分的概率为
( )
图1
A.
B.
C.
D.
4.某学校为了解学生大课间体育活动的情况,随机抽取本校部分学生进行调查,整理收集到的数据,绘制成如图2所示的统计图.小明随机调查一名学生,他喜欢“踢毽子”的概率是
( )
图2
A.
B.
C.
D.
5.一个盒子中装有四张完全相同的卡片,分别写着2
cm,3
cm,4
cm和5
cm,盒子外有两张卡片,分别写着3
cm和5
cm.现从盒子中随机取出一张卡片,与盒子外的两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,那么这三条线段能构成三角形的概率是
( )
A.
B.
C.
D.
类型二 用列表法、画树状图法求概率
6.在一个不透明的袋子里装有两个红球和两个黄球,它们除颜色不同外其余都相同.从中随机摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,两次都摸到黄球的概率是
( )
A.
B.
C.
D.
7.[2020·海淀区模拟]
从2020年5月1日起,北京正式施行“垃圾分类”,如图3是生活中的四个不同的垃圾分类投放桶.小明投放了两袋垃圾,不同类的概率是
( )
图3
A.
B.
C.
D.
类型三 概率与游戏公平性
8.现有A,B两个不透明的袋子,分别装有3个除颜色外其余完全相同的小球,其中A袋中装有2个白球,1个红球;B袋中装有2个红球,1个白球.小林和小华商定了一个游戏规则:从摇匀后的A,B两袋中各随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画树状图法,说明这个游戏对双方是否公平.
类型四 用频率估计概率
9.[2020·密云区二模]
新冠疫情发生以来,为保证防控期间的口罩供应,某公司加紧转产,开设多条生产线争分夺秒赶制口罩,从最初转产时的陌生,到正式投产后达成日均生产100万个口罩的产能.不仅效率高,而且口罩送检合格率也不断提升,真正体现了“大国速度”.以下是质监局对一批口罩进行质量抽检的相关数据,统计如下:
抽检数量n/个
20
50
100
200
500
1000
2000
5000
10000
合格数量m/个
19
46
93
185
459
922
1840
4595
9213
口罩合格率
0.950
0.920
0.930
0.925
0.918
0.922
0.920
0.919
0.921
下面四个推断合理的是
( )
A.当抽检口罩的数量是10000个时,口罩合格的数量是9213个,所以这批口罩中“口罩合格”的概率是0.921
B.由于抽检口罩的数量分别是50个和2000个时,口罩合格率均是0.920,所以可以估计这批口罩中“口罩合格”的概率是0.920
C.随着抽检数量的增加,“口罩合格”的频率总在0.920附近摆动,显示出一定的稳定性,所以可以估计这批口罩中“口罩合格”的概率是0.920
D.当抽检口罩的数量达到20000个时,“口罩合格”的概率一定是0.921
类型五 概率在实际生活中的应用
10.有两把不同的锁和三把钥匙,其中两把钥匙能打开同一把锁,第三把钥匙能打开另一把锁.任意取出一把钥匙去开任意的一把锁,一次能打开锁的概率是 .?
11.为了备战九年级物理、化学实验操作考试,某校对九年级学生进行了模拟训练.物理、化学各有4个不同的操作实验题目,物理用号码①,②,③,④代表,化学用字母a,b,c,d代表.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.
(1)请用画树状图法或列表法表示某个同学抽签的各种可能情况;
(2)小张同学对物理的①,②和化学的b,c号实验准备得较好,他同时抽到两科都准备得较好的实验题目的概率是多少?
类型六 概率与其他知识的综合应用
12.如图4,电路图上有四个开关A,B,C,D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光.
(1)任意闭合其中一个开关,则小灯泡发光的概率为 ;?
(2)任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.
图4
类型七 数学活动
13.在一个口袋中有4个完全相同的小球,把它们分别标上数字-1,0,1,2,随机地摸出一个小球记录数字,然后放回,再随机地摸出一个小球记录数字.求下列事件发生的概率:
(1)两次摸到的小球上的数字都是正数的概率P(A);
(2)两次摸到的小球上的数字和等于0的概率P(B).
答案
1.B 2.C 3.C 4.A
5.D 6.C 7.D
8.解:列表如下:
B
A
红1
红2
白
白1
(白1,红1)
(白1,红2)
(白1,白)
白2
(白2,红1)
(白2,红2)
(白2,白)
红
(红,红1)
(红,红2)
(红,白)
由上表可知,一共有9种等可能的结果,其中颜色相同的结果有4种,颜色不同的结果有5种.
∴P(颜色相同)=,P(颜色不同)=.
∵<,∴这个游戏对双方不公平.
9.C 10.
11.解:(1)画树状图如下:
或列表如下:
化学
物理
a
b
c
d
①
(①,a)
(①,b)
(①,c)
(①,d)
②
(②,a)
(②,b)
(②,c)
(②,d)
③
(③,a)
(③,b)
(③,c)
(③,d)
④
(④,a)
(④,b)
(④,c)
(④,d)
(2)由(1)可得所有等可能的情况共有16种,小张同学同时抽到两科都准备得较好的实验题目[即(①,b),(②,b),(①,c),(②,c)]的概率P==.
12.解:(1)
(2)画出树状图如下:
任意闭合其中两个开关的等可能的情况共有12种,其中能使小灯泡发光的情况有6种,所以P(小灯泡发光)==.
13.解:(1)画树状图如下:
所有可能出现的等可能结果共有16种,两个数字都是正数的结果有4种,所以P(A)==.
(2)由(1),得所有可能出现的等可能结果共有16种,其中两次的数字和为0的结果有3种,所以P(B)=.
