第三章位置与坐标单元测试题-2021——2022学年北师大版八年级数学上册(Word版含答案)
文档属性
| 名称 | 第三章位置与坐标单元测试题-2021——2022学年北师大版八年级数学上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 254.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 16:58:42 | ||
图片预览


文档简介
第三章 位置与坐标
一、选择题(每小题4分,共24分)
1.下列能确定一个地点的位置的是( )
A.偏西50°,1000
m
B.东南方向,距此800
m
C.距此1000
m
D.正北方向
2.在平面直角坐标系中,将点A(0,0),B(2,4),C(3,0),D(5,4),E(6,0)顺次连接起来,此图形像英文字母( )
A.V
B.E
C.W
D.M
3.若点P(a,b)在第四象限,则点M(b-a,a-b)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.已知点A(m+1,-2)和点B(3,m-1),若直线AB∥x轴,则m的值为( )
A.2
B.-4
C.-1
D.3
5.若点P(1,a)与点Q关于x轴对称,点Q与点R(-b,2)关于y轴对称,则代数式(a+b)2021的值为
( )
A.-1
B.1
C.-2
D.2
6.小明为画一个零件的轴截面(如图3-2-1①),以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图1所示的平面直角坐标系.若坐标轴的单位长度取1
mm,则图中转折点P的坐标表示正确的是( )
图1
A.(5,30)
B.(8,10)
C.(9,10)
D.(10,10)
二、填空题(每小题4分,共20分)
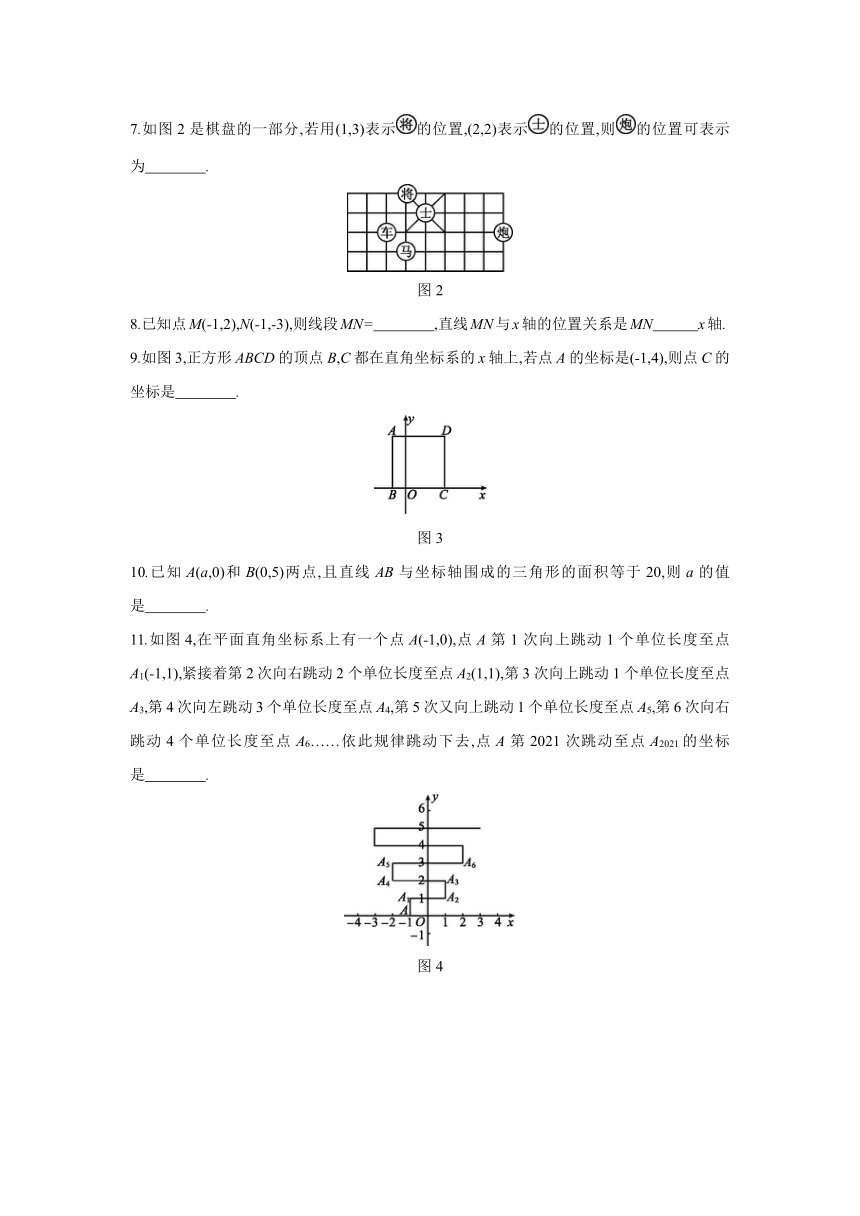
7.如图2是棋盘的一部分,若用(1,3)表示的位置,(2,2)表示的位置,则的位置可表示为 .?
图2
8.已知点M(-1,2),N(-1,-3),则线段MN= ,直线MN与x轴的位置关系是MN x轴.?
9.如图3,正方形ABCD的顶点B,C都在直角坐标系的x轴上,若点A的坐标是(-1,4),则点C的坐标是 .?
图3
10.已知A(a,0)和B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于20,则a的值是
.?
11.如图4,在平面直角坐标系上有一个点A(-1,0),点A第1次向上跳动1个单位长度至点A1(-1,1),紧接着第2次向右跳动2个单位长度至点A2(1,1),第3次向上跳动1个单位长度至点A3,第4次向左跳动3个单位长度至点A4,第5次又向上跳动1个单位长度至点A5,第6次向右跳动4个单位长度至点A6……依此规律跳动下去,点A第2021次跳动至点A2021的坐标是 .?
图4
三、解答题(共56分)
12.(10分)周末,小明、小华、小丽三名同学相约到政府广场上玩.出发前,他们每人带了一张利用平面直角坐标系画出的草图,其中市政府的坐标是(2,0),某酒店的坐标是(4,2).
(1)如图5所示是省略了平面直角坐标系后的示意图,请你根据上述信息,画出这个平面直角坐标系;
(2)在此坐标系中,某研究所的坐标是 ,公交车站的坐标是 ;?
(3)小华、小丽两人到了升旗台附近,这时还没有看见小明,于是打电话问小明的位置,小明说他所在位置的坐标为(5,-4),请你在图中用字母A标出小明的位置;
(4)在(3)的前提下,过了一段时间,又打电话问小明的位置,小明说他向北走了3个单位长度,此时小明所在位置的坐标是 .?
图5
13.(10分)如图6所示,△ABC在正方形网格中,若点A的坐标为(0,3),点B的坐标为(-3,-1),按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点C的坐标;
(3)作出△ABC关于x轴对称的图形△A'B'C'(不用写作法).
图6
14.(12分)已知点P(2m-6,m+2).
(1)若点P在y轴上,则点P的坐标为 ;?
(2)若点P的纵坐标比横坐标大6,则点P在第几象限?
(3)若点P和点Q都在过点A(2,3)且与x轴平行的直线上,AQ=3,求点P,Q的坐标.
15.(12分)已知Rt△ABC两个非直角顶点的坐标分别为A(-1,0),B(4,0),且AC=4.
求:(1)△ABC的面积;
(2)顶点C的坐标.
16.(12分)如图7,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a,b满足+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动一周.
(1)点B的坐标为 ;当点P移动3.5秒时,点P的坐标为 .?
(2)在移动过程中,当点P到x轴的距离为4个单位长度时,求点P移动的时间.
(3)在O-C-B线路的移动过程中,当△OBP的面积是10时,求点P移动的时间.
图7
答案1.B 2.D
3.B [解析]
因为点P(a,b)在第四象限,所以a>0,b<0,所以b-a<0,a-b>0,所以点M(b-a,a-b)在第二象限.
4.C [解析]
因为点A(m+1,-2),B(3,m-1),直线AB∥x轴,所以m-1=-2,解得m=-1.故选C.
5.A
6.C [解析]
如图,过点B作BD⊥y轴于点D,
所以CD=50÷2-16=9,OA=OD-AD=40-30=10,所以P(9,10).
7.(6,1) 8.5 ⊥
9.(3,0) [解析]
因为四边形ABCD为正方形,点A的坐标是(-1,4),所以BC=AB=4,OB=1,所以OC=BC-OB=4-1=3,所以点C的坐标为(3,0).
10.8或-8
11.(-506,1011) [解析]
设点A第n次跳动后至点An,根据部分点An坐标的变化找出规律“A4n(-n-1,2n),A4n+1(-n-1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数)”,依此规律结合2020=505×4,可得A2021(-505-1,505×2+1),即(-506,1011).
12.解:(1)如图所示,以升旗台为坐标原点建立平面直角坐标系.
(2)(-1,-3) (0,3)
(3)点A如图所示.
(4)(5,-1)
13.解:(1)所建立的平面直角坐标系如图所示.
(2)点C的坐标为(1,1).
(3)△A'B'C'如图所示.
14.解:(1)因为点P在y轴上,所以2m-6=0,解得m=3,所以点P的坐标为(0,5).故答案为(0,5).
(2)根据题意,得2m-6+6=m+2,解得m=2,
所以点P的坐标为(-2,4).
所以点P在第二象限.
(3)因为点P和点Q都在过点A(2,3)且与x轴平行的直线上,所以点P和点Q的纵坐标都为3.
所以m+2=3,解得m=1.
所以点P的坐标为(-4,3).
因为AQ=3,所以点Q的横坐标为-1或5.
所以点Q的坐标为(-1,3)或(5,3).
15.(1)6
(2)(2.2,2.4)或(2.2,-2.4)
16.解(1)(4,6) (1,6)
(2)由题意可得,在移动过程中,当点P到x轴的距离为4个单位长度时,存在两种情况:
第一种情况,当点P在OC上时,
点P移动的时间是4÷2=2(秒);
第二种情况,当点P在BA上时.
点P移动的时间是(6+4+2)÷2=6(秒).
故在移动过程中,当点P到x轴的距离为4个单位长度时,点P移动的时间是2秒或6秒.
(3)如图①所示,当点P在OC上时.
因为△OBP的面积是10,
所以BC·OP=10,即×4×OP=10,
解得OP=5,
所以此时点P移动的时间为5÷2=2.5(秒);
如图②所示,当点P在BC上时.
因为△OBP的面积为10,
所以OC·BP=10,即×6×BP=10,
解得BP=,
所以CP=4-=,
所以此时点P移动的时间为6+÷2=(秒).
综上,点P移动的时间为2.5秒或秒.
一、选择题(每小题4分,共24分)
1.下列能确定一个地点的位置的是( )
A.偏西50°,1000
m
B.东南方向,距此800
m
C.距此1000
m
D.正北方向
2.在平面直角坐标系中,将点A(0,0),B(2,4),C(3,0),D(5,4),E(6,0)顺次连接起来,此图形像英文字母( )
A.V
B.E
C.W
D.M
3.若点P(a,b)在第四象限,则点M(b-a,a-b)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.已知点A(m+1,-2)和点B(3,m-1),若直线AB∥x轴,则m的值为( )
A.2
B.-4
C.-1
D.3
5.若点P(1,a)与点Q关于x轴对称,点Q与点R(-b,2)关于y轴对称,则代数式(a+b)2021的值为
( )
A.-1
B.1
C.-2
D.2
6.小明为画一个零件的轴截面(如图3-2-1①),以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图1所示的平面直角坐标系.若坐标轴的单位长度取1
mm,则图中转折点P的坐标表示正确的是( )
图1
A.(5,30)
B.(8,10)
C.(9,10)
D.(10,10)
二、填空题(每小题4分,共20分)
7.如图2是棋盘的一部分,若用(1,3)表示的位置,(2,2)表示的位置,则的位置可表示为 .?
图2
8.已知点M(-1,2),N(-1,-3),则线段MN= ,直线MN与x轴的位置关系是MN x轴.?
9.如图3,正方形ABCD的顶点B,C都在直角坐标系的x轴上,若点A的坐标是(-1,4),则点C的坐标是 .?
图3
10.已知A(a,0)和B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于20,则a的值是
.?
11.如图4,在平面直角坐标系上有一个点A(-1,0),点A第1次向上跳动1个单位长度至点A1(-1,1),紧接着第2次向右跳动2个单位长度至点A2(1,1),第3次向上跳动1个单位长度至点A3,第4次向左跳动3个单位长度至点A4,第5次又向上跳动1个单位长度至点A5,第6次向右跳动4个单位长度至点A6……依此规律跳动下去,点A第2021次跳动至点A2021的坐标是 .?
图4
三、解答题(共56分)
12.(10分)周末,小明、小华、小丽三名同学相约到政府广场上玩.出发前,他们每人带了一张利用平面直角坐标系画出的草图,其中市政府的坐标是(2,0),某酒店的坐标是(4,2).
(1)如图5所示是省略了平面直角坐标系后的示意图,请你根据上述信息,画出这个平面直角坐标系;
(2)在此坐标系中,某研究所的坐标是 ,公交车站的坐标是 ;?
(3)小华、小丽两人到了升旗台附近,这时还没有看见小明,于是打电话问小明的位置,小明说他所在位置的坐标为(5,-4),请你在图中用字母A标出小明的位置;
(4)在(3)的前提下,过了一段时间,又打电话问小明的位置,小明说他向北走了3个单位长度,此时小明所在位置的坐标是 .?
图5
13.(10分)如图6所示,△ABC在正方形网格中,若点A的坐标为(0,3),点B的坐标为(-3,-1),按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点C的坐标;
(3)作出△ABC关于x轴对称的图形△A'B'C'(不用写作法).
图6
14.(12分)已知点P(2m-6,m+2).
(1)若点P在y轴上,则点P的坐标为 ;?
(2)若点P的纵坐标比横坐标大6,则点P在第几象限?
(3)若点P和点Q都在过点A(2,3)且与x轴平行的直线上,AQ=3,求点P,Q的坐标.
15.(12分)已知Rt△ABC两个非直角顶点的坐标分别为A(-1,0),B(4,0),且AC=4.
求:(1)△ABC的面积;
(2)顶点C的坐标.
16.(12分)如图7,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a,b满足+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动一周.
(1)点B的坐标为 ;当点P移动3.5秒时,点P的坐标为 .?
(2)在移动过程中,当点P到x轴的距离为4个单位长度时,求点P移动的时间.
(3)在O-C-B线路的移动过程中,当△OBP的面积是10时,求点P移动的时间.
图7
答案1.B 2.D
3.B [解析]
因为点P(a,b)在第四象限,所以a>0,b<0,所以b-a<0,a-b>0,所以点M(b-a,a-b)在第二象限.
4.C [解析]
因为点A(m+1,-2),B(3,m-1),直线AB∥x轴,所以m-1=-2,解得m=-1.故选C.
5.A
6.C [解析]
如图,过点B作BD⊥y轴于点D,
所以CD=50÷2-16=9,OA=OD-AD=40-30=10,所以P(9,10).
7.(6,1) 8.5 ⊥
9.(3,0) [解析]
因为四边形ABCD为正方形,点A的坐标是(-1,4),所以BC=AB=4,OB=1,所以OC=BC-OB=4-1=3,所以点C的坐标为(3,0).
10.8或-8
11.(-506,1011) [解析]
设点A第n次跳动后至点An,根据部分点An坐标的变化找出规律“A4n(-n-1,2n),A4n+1(-n-1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数)”,依此规律结合2020=505×4,可得A2021(-505-1,505×2+1),即(-506,1011).
12.解:(1)如图所示,以升旗台为坐标原点建立平面直角坐标系.
(2)(-1,-3) (0,3)
(3)点A如图所示.
(4)(5,-1)
13.解:(1)所建立的平面直角坐标系如图所示.
(2)点C的坐标为(1,1).
(3)△A'B'C'如图所示.
14.解:(1)因为点P在y轴上,所以2m-6=0,解得m=3,所以点P的坐标为(0,5).故答案为(0,5).
(2)根据题意,得2m-6+6=m+2,解得m=2,
所以点P的坐标为(-2,4).
所以点P在第二象限.
(3)因为点P和点Q都在过点A(2,3)且与x轴平行的直线上,所以点P和点Q的纵坐标都为3.
所以m+2=3,解得m=1.
所以点P的坐标为(-4,3).
因为AQ=3,所以点Q的横坐标为-1或5.
所以点Q的坐标为(-1,3)或(5,3).
15.(1)6
(2)(2.2,2.4)或(2.2,-2.4)
16.解(1)(4,6) (1,6)
(2)由题意可得,在移动过程中,当点P到x轴的距离为4个单位长度时,存在两种情况:
第一种情况,当点P在OC上时,
点P移动的时间是4÷2=2(秒);
第二种情况,当点P在BA上时.
点P移动的时间是(6+4+2)÷2=6(秒).
故在移动过程中,当点P到x轴的距离为4个单位长度时,点P移动的时间是2秒或6秒.
(3)如图①所示,当点P在OC上时.
因为△OBP的面积是10,
所以BC·OP=10,即×4×OP=10,
解得OP=5,
所以此时点P移动的时间为5÷2=2.5(秒);
如图②所示,当点P在BC上时.
因为△OBP的面积为10,
所以OC·BP=10,即×6×BP=10,
解得BP=,
所以CP=4-=,
所以此时点P移动的时间为6+÷2=(秒).
综上,点P移动的时间为2.5秒或秒.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
