2021——2022学年华东师大版八年级数学上册第13章全等三角形单元测试题(word解析版)
文档属性
| 名称 | 2021——2022学年华东师大版八年级数学上册第13章全等三角形单元测试题(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 143.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
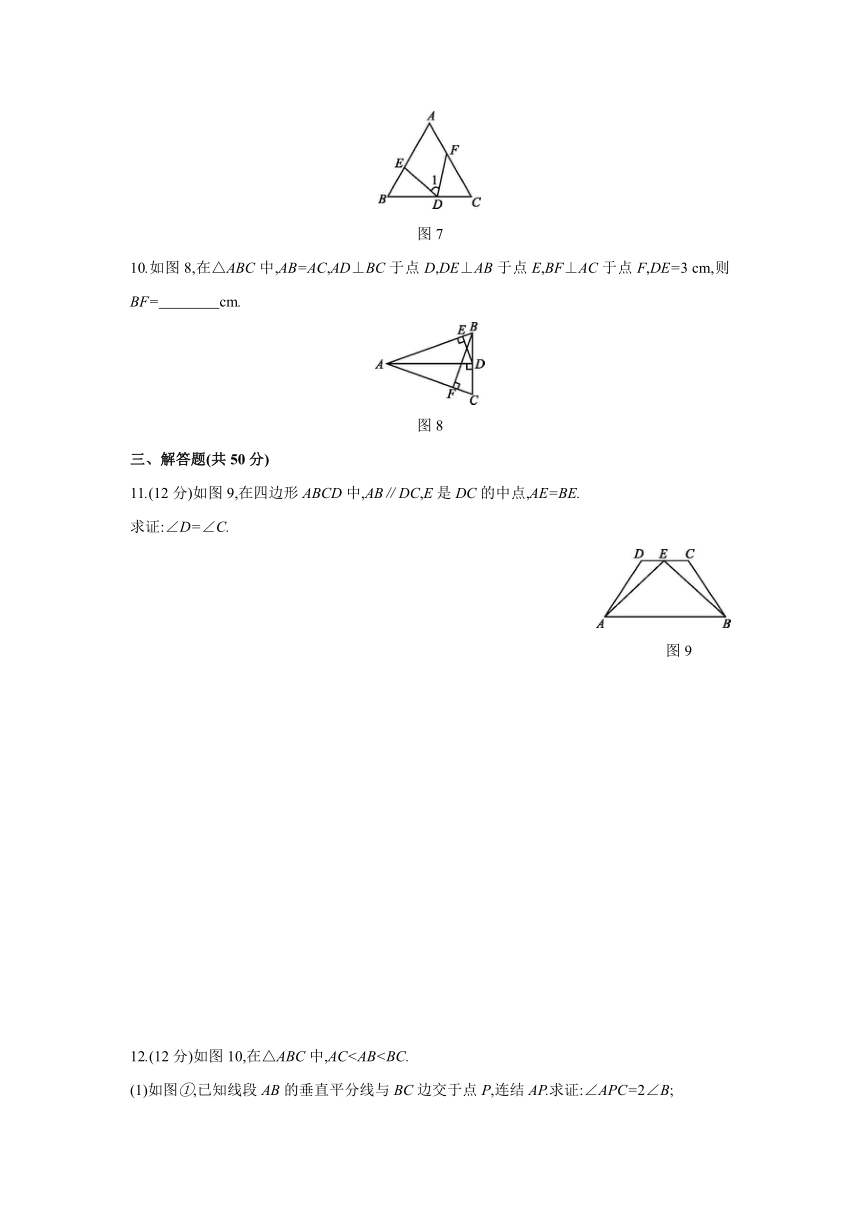
| 科目 | 数学 | ||
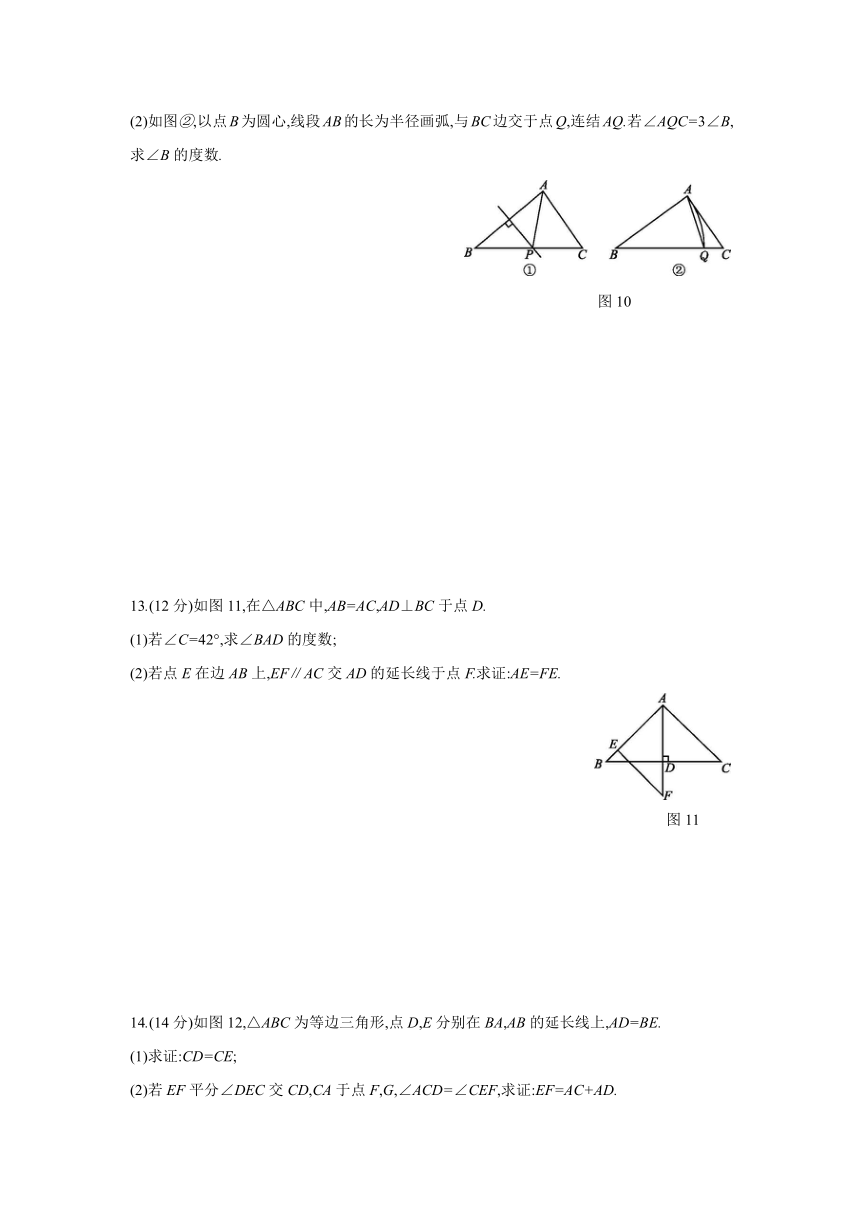
| 更新时间 | 2021-07-01 00:00:00 | ||
图片预览


文档简介
第13章 全等三角形
一、选择题(每题5分,共25分)
1.若一个三角形每条边上的中线都是这条边上的高,则对该三角形的形状描述最准确的是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等边三角形
2.如图1,有两把完全相同的直尺,一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠AOB的平分线.”他这样做的依据是( )
图1
A.角平分线上的点到这个角两边的距离相等
B.角的内部到角两边距离相等的点在角的平分线上
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
3.如图2所示,AD为∠BAC的平分线,添加下列一个条件后,仍无法判定△ABD≌△ACD的是( )
图2
A.∠B=∠C
B.BD=CD
C.∠BDA=∠CDA
D.AB=AC
4.如图3所示,D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
图3
A.AC>BC
B.AC=BC
C.∠A>∠ABC
D.∠A=∠ABC
5.如图4,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线与AC,AD,AB分别交于点E,O,F,则图中全等三角形有( )
图4
A.1对
B.2对
C.3对
D.4对
二、填空题(每题5分,共25分)
6.命题“如果两个实数相等,那么它们的平方相等”的逆命题是
,逆命题是 (填“真”或“假”)命题.?
7.如图5所示,已知点B,F,C,E在同一条直线上,△ABC≌△DFE,且AC与DE是对应边.若BE=14
cm,FC=4
cm,则BC= .?
图5
8.如图6,在等腰三角形纸片ABC中,AB=AC,∠A=50°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE= °.?
图6
9.如图7,在△ABC中,点D在BC边上,∠B=∠C=∠1,BD=CF=3,BE=2,则BC= .?
图7
10.如图8,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=3
cm,则BF= cm.?
图8
三、解答题(共50分)
11.(12分)如图9,在四边形ABCD中,AB∥DC,E是DC的中点,AE=BE.
求证:∠D=∠C.
图9
12.(12分)如图10,在△ABC中,AC(1)如图①,已知线段AB的垂直平分线与BC边交于点P,连结AP.求证:∠APC=2∠B;
(2)如图②,以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连结AQ.若∠AQC=3∠B,求∠B的度数.
图10
13.(12分)如图11,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在边AB上,EF∥AC交AD的延长线于点F.求证:AE=FE.
图11
14.(14分)如图12,△ABC为等边三角形,点D,E分别在BA,AB的延长线上,AD=BE.
(1)求证:CD=CE;
(2)若EF平分∠DEC交CD,CA于点F,G,∠ACD=∠CEF,求证:EF=AC+AD.
图12
答案
1.D
2.B [解析]
如图所示,过点P作PE⊥OA于点E,PF⊥OB于点F.
又∵两把完全相同的长方形直尺的宽度相等,∴PE=PF,∴OP平分∠AOB(角的内部到角两边距离相等的点在角的平分线上).故选B.
3.B [解析]
∵AD为∠BAC的平分线,
∴∠BAD=∠CAD.
又∵AD=AD,
∴若添加∠B=∠C,则△ABD≌△ACD(A.A.S.),故选项A不符合题意;
若添加BD=CD,则无法判定△ABD≌△ACD,故选项B符合题意;
若添加∠BDA=∠CDA,则△ABD≌△ACD(A.S.A.),故选项C不符合题意;
若添加AB=AC,则△ABD≌△ACD(S.A.S.),故选项D不符合题意.
故选B.
4.A [解析]
∵AD=BD,∴∠A=∠ABD,
∴∠ABC>∠A,
∴C选项和D选项错误;
∵AC=AD+CD=BD+CD,BD+CD>BC,
∴AC>BC,∴A选项正确,B选项错误.
故选A.
5.D [解析]
∵AB=AC,D为BC的中点,
∴CD=BD,∠BDO=∠CDO=90°.
在△ABD和△ACD中,
∵AB=AC,AD=AD,BD=CD,
∴△ABD≌△ACD.
∵EF垂直平分AC,
∴OA=OC,AE=CE.
在△AOE和△COE中,
∵OA=OC,OE=OE,AE=CE,
∴△AOE≌△COE.
在△BOD和△COD中,
∵BD=CD,∠BDO=∠CDO,OD=OD,
∴△BOD≌△COD,
∴OB=OC.
在△AOC和△AOB中,
∵AC=AB,OA=OA,OC=OB,
∴△AOC≌△AOB.
故选D.
6.如果两个实数的平方相等,那么这两个实数相等 假
[解析]
命题“如果两个实数相等,那么它们的平方相等”的逆命题是“如果两个实数的平方相等,那么这两个实数相等”,当a2=b2时,a=±b,则逆命题是假命题.
7.9
cm
8.15 [解析]
∵AB=AC,∠A=50°,
∴∠ACB=∠ABC=×(180°-50°)=65°.
∵将△ABC折叠,使点A落在点B处,折痕为DE,∠A=50°,∴∠ABE=∠A=50°,
∴∠CBE=∠ABC-∠ABE=65°-50°=15°.
故答案为15.
9.5 [解析]
∵∠EDC=∠B+∠BED=∠1+∠CDF,且∠1=∠B,
∴∠BED=∠CDF.
在△BED和△CDF中,
∵∠B=∠C,∠BED=∠CDF,BD=CF,
∴△BED≌△CDF(A.A.S.),
∴CD=BE=2.
又∵BD=3,
∴BC=BD+CD=3+2=5.
故答案为5.
10.6 [解析]
∵AB=AC,AD⊥BC,∴BD=CD,∴S△ABC=2S△ABD=2×AB·DE=AB·DE=3AB.
∵S△ABC=AC·BF,∴AC·BF=3AB.∵AC=AB,∴BF=3,∴BF=6.故答案为6.
11.证明:∵AE=BE,∴∠EAB=∠EBA.
∵AB∥DC,∴∠DEA=∠EAB,∠CEB=∠EBA,∴∠DEA=∠CEB.
∵E是DC的中点,∴DE=CE.
在△ADE和△BCE中,
∵DE=CE,∠DEA=∠CEB,AE=BE,
∴△ADE≌△BCE(S.A.S.),∴∠D=∠C.
12.解:(1)证明:∵线段AB的垂直平分线与BC边交于点P,∴PA=PB,∴∠B=∠BAP.
∵∠APC=∠B+∠BAP,∴∠APC=2∠B.
(2)根据题意可知BA=BQ,∴∠BAQ=∠BQA.
∵∠AQC=3∠B,∠AQC=∠B+∠BAQ,
∴∠BAQ=∠BQA=2∠B.
∵∠BAQ+∠BQA+∠B=180°,
∴5∠B=180°,
∴∠B=36°.
13.解:(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°.
又∵∠C=42°,
∴∠BAD=∠CAD=90°-42°=48°.
(2)证明:∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD.
∵EF∥AC,
∴∠F=∠CAD,
∴∠BAD=∠F,
∴AE=FE.
14.证明:(1)∵△ABC为等边三角形,
∴∠BAC=∠ABC=∠ACB=60°,AB=BC=AC,
∴∠DAC=∠EBC=120°.
又∵AD=BE,
∴△ACD≌△BCE(S.A.S.),
∴CD=CE.
(2)∵△ACD≌△BCE,
∴∠ACD=∠BCE,AD=BE.
∵EF平分∠DEC,
∴∠DEF=∠CEF.
∵∠ACD=∠CEF,
∴∠ACD=∠CEF=∠DEF=∠BCE.
∵∠EGC=∠AEG+∠BAC=∠AEG+60°,∠ECG=∠BCE+∠ACB=∠BCE+60°,
∴∠EGC=∠ECG,
∴EC=EG.
∵∠EGC=∠AEG+∠BAC=∠EFC+∠ACD,
∴∠BAC=∠EFC,即∠EAG=∠EFC.
又∵∠CEF=∠GEA,EC=EG,
∴△EFC≌△EAG(A.A.S.),
∴EF=EA.
∵EA=AB+BE=AC+AD,
∴EF=AC+AD.
一、选择题(每题5分,共25分)
1.若一个三角形每条边上的中线都是这条边上的高,则对该三角形的形状描述最准确的是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等边三角形
2.如图1,有两把完全相同的直尺,一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠AOB的平分线.”他这样做的依据是( )
图1
A.角平分线上的点到这个角两边的距离相等
B.角的内部到角两边距离相等的点在角的平分线上
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
3.如图2所示,AD为∠BAC的平分线,添加下列一个条件后,仍无法判定△ABD≌△ACD的是( )
图2
A.∠B=∠C
B.BD=CD
C.∠BDA=∠CDA
D.AB=AC
4.如图3所示,D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
图3
A.AC>BC
B.AC=BC
C.∠A>∠ABC
D.∠A=∠ABC
5.如图4,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线与AC,AD,AB分别交于点E,O,F,则图中全等三角形有( )
图4
A.1对
B.2对
C.3对
D.4对
二、填空题(每题5分,共25分)
6.命题“如果两个实数相等,那么它们的平方相等”的逆命题是
,逆命题是 (填“真”或“假”)命题.?
7.如图5所示,已知点B,F,C,E在同一条直线上,△ABC≌△DFE,且AC与DE是对应边.若BE=14
cm,FC=4
cm,则BC= .?
图5
8.如图6,在等腰三角形纸片ABC中,AB=AC,∠A=50°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE= °.?
图6
9.如图7,在△ABC中,点D在BC边上,∠B=∠C=∠1,BD=CF=3,BE=2,则BC= .?
图7
10.如图8,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=3
cm,则BF= cm.?
图8
三、解答题(共50分)
11.(12分)如图9,在四边形ABCD中,AB∥DC,E是DC的中点,AE=BE.
求证:∠D=∠C.
图9
12.(12分)如图10,在△ABC中,AC
(2)如图②,以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连结AQ.若∠AQC=3∠B,求∠B的度数.
图10
13.(12分)如图11,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在边AB上,EF∥AC交AD的延长线于点F.求证:AE=FE.
图11
14.(14分)如图12,△ABC为等边三角形,点D,E分别在BA,AB的延长线上,AD=BE.
(1)求证:CD=CE;
(2)若EF平分∠DEC交CD,CA于点F,G,∠ACD=∠CEF,求证:EF=AC+AD.
图12
答案
1.D
2.B [解析]
如图所示,过点P作PE⊥OA于点E,PF⊥OB于点F.
又∵两把完全相同的长方形直尺的宽度相等,∴PE=PF,∴OP平分∠AOB(角的内部到角两边距离相等的点在角的平分线上).故选B.
3.B [解析]
∵AD为∠BAC的平分线,
∴∠BAD=∠CAD.
又∵AD=AD,
∴若添加∠B=∠C,则△ABD≌△ACD(A.A.S.),故选项A不符合题意;
若添加BD=CD,则无法判定△ABD≌△ACD,故选项B符合题意;
若添加∠BDA=∠CDA,则△ABD≌△ACD(A.S.A.),故选项C不符合题意;
若添加AB=AC,则△ABD≌△ACD(S.A.S.),故选项D不符合题意.
故选B.
4.A [解析]
∵AD=BD,∴∠A=∠ABD,
∴∠ABC>∠A,
∴C选项和D选项错误;
∵AC=AD+CD=BD+CD,BD+CD>BC,
∴AC>BC,∴A选项正确,B选项错误.
故选A.
5.D [解析]
∵AB=AC,D为BC的中点,
∴CD=BD,∠BDO=∠CDO=90°.
在△ABD和△ACD中,
∵AB=AC,AD=AD,BD=CD,
∴△ABD≌△ACD.
∵EF垂直平分AC,
∴OA=OC,AE=CE.
在△AOE和△COE中,
∵OA=OC,OE=OE,AE=CE,
∴△AOE≌△COE.
在△BOD和△COD中,
∵BD=CD,∠BDO=∠CDO,OD=OD,
∴△BOD≌△COD,
∴OB=OC.
在△AOC和△AOB中,
∵AC=AB,OA=OA,OC=OB,
∴△AOC≌△AOB.
故选D.
6.如果两个实数的平方相等,那么这两个实数相等 假
[解析]
命题“如果两个实数相等,那么它们的平方相等”的逆命题是“如果两个实数的平方相等,那么这两个实数相等”,当a2=b2时,a=±b,则逆命题是假命题.
7.9
cm
8.15 [解析]
∵AB=AC,∠A=50°,
∴∠ACB=∠ABC=×(180°-50°)=65°.
∵将△ABC折叠,使点A落在点B处,折痕为DE,∠A=50°,∴∠ABE=∠A=50°,
∴∠CBE=∠ABC-∠ABE=65°-50°=15°.
故答案为15.
9.5 [解析]
∵∠EDC=∠B+∠BED=∠1+∠CDF,且∠1=∠B,
∴∠BED=∠CDF.
在△BED和△CDF中,
∵∠B=∠C,∠BED=∠CDF,BD=CF,
∴△BED≌△CDF(A.A.S.),
∴CD=BE=2.
又∵BD=3,
∴BC=BD+CD=3+2=5.
故答案为5.
10.6 [解析]
∵AB=AC,AD⊥BC,∴BD=CD,∴S△ABC=2S△ABD=2×AB·DE=AB·DE=3AB.
∵S△ABC=AC·BF,∴AC·BF=3AB.∵AC=AB,∴BF=3,∴BF=6.故答案为6.
11.证明:∵AE=BE,∴∠EAB=∠EBA.
∵AB∥DC,∴∠DEA=∠EAB,∠CEB=∠EBA,∴∠DEA=∠CEB.
∵E是DC的中点,∴DE=CE.
在△ADE和△BCE中,
∵DE=CE,∠DEA=∠CEB,AE=BE,
∴△ADE≌△BCE(S.A.S.),∴∠D=∠C.
12.解:(1)证明:∵线段AB的垂直平分线与BC边交于点P,∴PA=PB,∴∠B=∠BAP.
∵∠APC=∠B+∠BAP,∴∠APC=2∠B.
(2)根据题意可知BA=BQ,∴∠BAQ=∠BQA.
∵∠AQC=3∠B,∠AQC=∠B+∠BAQ,
∴∠BAQ=∠BQA=2∠B.
∵∠BAQ+∠BQA+∠B=180°,
∴5∠B=180°,
∴∠B=36°.
13.解:(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°.
又∵∠C=42°,
∴∠BAD=∠CAD=90°-42°=48°.
(2)证明:∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD.
∵EF∥AC,
∴∠F=∠CAD,
∴∠BAD=∠F,
∴AE=FE.
14.证明:(1)∵△ABC为等边三角形,
∴∠BAC=∠ABC=∠ACB=60°,AB=BC=AC,
∴∠DAC=∠EBC=120°.
又∵AD=BE,
∴△ACD≌△BCE(S.A.S.),
∴CD=CE.
(2)∵△ACD≌△BCE,
∴∠ACD=∠BCE,AD=BE.
∵EF平分∠DEC,
∴∠DEF=∠CEF.
∵∠ACD=∠CEF,
∴∠ACD=∠CEF=∠DEF=∠BCE.
∵∠EGC=∠AEG+∠BAC=∠AEG+60°,∠ECG=∠BCE+∠ACB=∠BCE+60°,
∴∠EGC=∠ECG,
∴EC=EG.
∵∠EGC=∠AEG+∠BAC=∠EFC+∠ACD,
∴∠BAC=∠EFC,即∠EAG=∠EFC.
又∵∠CEF=∠GEA,EC=EG,
∴△EFC≌△EAG(A.A.S.),
∴EF=EA.
∵EA=AB+BE=AC+AD,
∴EF=AC+AD.
