1.3 公式法 课件(共34张PPT)
图片预览











文档简介
第一章 因式分解
3 公式法
知识点一 用平方差公式分解因式
法则
字母表示
举例
平方差公式
两个数的平方差,等于这两个数的和与这两个数的差的积
a2-b2=(a+b)(a-b)
4m2-9=(2m+3)(2m-3)
知识详解
(1)特点:等号左边是二项式,两项都是平方项,两项的符号相反;等号右边是两平方项的底数的和与底数的差的乘积.
(2)分解因式的时候,有公因式的先提公因式,提公因式后,如果剩下的多项式恰好可以表示成两项平方差的形式,那么就考虑运用平方差公式继续分解因式.
(3)公式中的a,b可以是单项式,也可以是多项式.
例1 把下列各式分解因式:
(1)-4m2+25n2;
(2)169(a+b)2-121(a-b)2.
例1 把下列各式分解因式:
(1)-4m2+25n2;
(2)169(a+b)2-121(a-b)2.
分析 (1)中的多项式可变为-(4m2-25n2),可写成-[(2m)2-(5n)2],从而利用平方差公式进行因式分解;(2)中的多项式可写成[13(a+b)]2-[11(a-b)]2,从而利用平方差公式进行因式分解.
解析 (1)-4m2+25n2
=-(4m2-25n2)
=-[(2m)2-(5n)2]
=-(2m+5n)(2m-5n)
(2)169(a+b)2-121(a-b)2
=[13(a+b)]2-[11(a-b)]2
=[13(a+b)+11(a-b)][13(a+b)-11(a-b)]
=(24a+2b)(2a+24b)
=4(12a+b)(a+12b)
解析 (1)-4m2+25n2
=-(4m2-25n2)
=-[(2m)2-(5n)2]
=-(2m+5n)(2m-5n)
(2)169(a+b)2-121(a-b)2
=[13(a+b)]2-[11(a-b)]2
=[13(a+b)+11(a-b)][13(a+b)-11(a-b)]
=(24a+2b)(2a+24b)
=4(12a+b)(a+12b)
点拨 运用平方差公式进行因式分解时,把多项式化成“平方差”的形式,以便明确哪项是公式中的a,哪项是公式中的b.
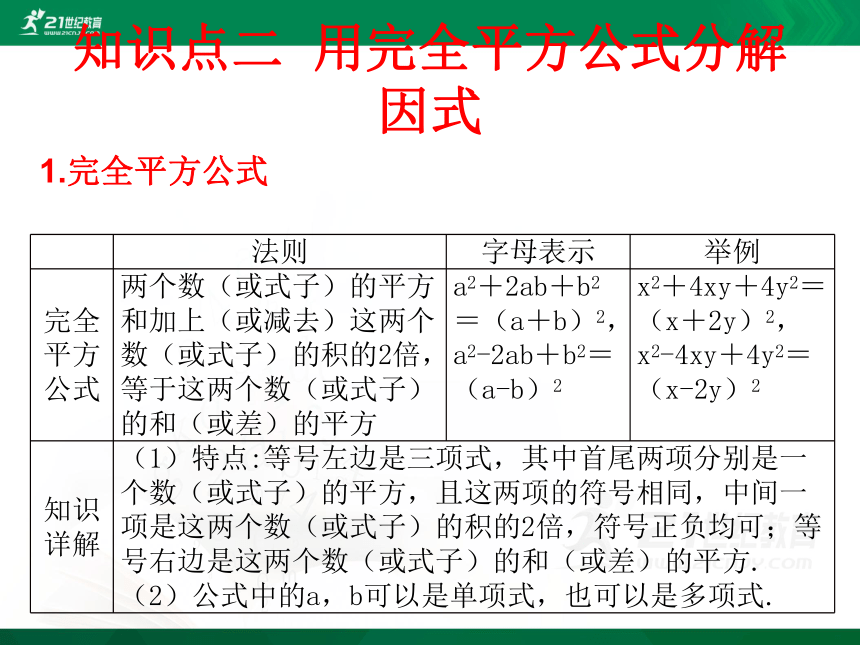
知识点二 用完全平方公式分解因式
1.完全平方公式
法则
字母表示
举例
完全平方公式
两个数(或式子)的平方和加上(或减去)这两个数(或式子)的积的2倍,等于这两个数(或式子)的和(或差)的平方
a2+2ab+b2=(a+b)2,a2-2ab+b2=(a-b)2
x2+4xy+4y2=(x+2y)2,x2-4xy+4y2=(x-2y)2
知识详解
(1)特点:等号左边是三项式,其中首尾两项分别是一个数(或式子)的平方,且这两项的符号相同,中间一项是这两个数(或式子)的积的2倍,符号正负均可;等号右边是这两个数(或式子)的和(或差)的平方.
(2)公式中的a,b可以是单项式,也可以是多项式.
2.公式法
通常我们把运用乘法公式进行因式分解的方法叫做公式法.
例2 分解因式:
(1)m2+14m+49;
(2)9x2-12x+4;
(3)a2+2a(b+c)+(b+c)2.
例2 分解因式:
(1)m2+14m+49;
(2)9x2-12x+4;
(3)a2+2a(b+c)+(b+c)2.
分析 (1)两个平方项是m2和72,可以用完全平方公式分解因式;(2)两个平方项分别为(3x)2和22,可以用完全平方公式分解因式;(3)两个平方项分别为a2和(b+c)2,可以用完全平方公式分解因式.
解析 (1)m2+14m+49=m2+2m×7+72=(m+7)2;(2)9x2-12x+4=(3x)2-2×3x×2+22=(3x-2)2;
(3)a2+2a(b+c)+(b+c)2=[a+(b+c)]2=(a+b+c)2.
解析 (1)m2+14m+49=m2+2m×7+72=(m+7)2;(2)9x2-12x+4=(3x)2-2×3x×2+22=(3x-2)2;
(3)a2+2a(b+c)+(b+c)2=[a+(b+c)]2=(a+b+c)2.
点拨 一个多项式可以利用完全平方公式分解因式时,这个多项式必须具备:(1)是一个三项式;(2)三项中有两项是两个数(或式子)的平方,第三项是这两个数(或式子)乘积的2倍或-2倍只有同时具备以上两个条件,才能用完全平方公式分解因式.
知识点三 综合应用各种方法分解因式
因为多项式的形式多种多样,所以因式分解的方法也有多种要迅速选择恰当的方法,必须注意从多项式的项数、各项符号、各项之间的关系等方面综合分析一般可遵循下列步骤进行:
知识点三 综合应用各种方法分解因式
因为多项式的形式多种多样,所以因式分解的方法也有多种要迅速选择恰当的方法,必须注意从多项式的项数、各项符号、各项之间的关系等方面综合分析一般可遵循下列步骤进行:
一提
看多项式的各项是否有公因式,若有,则应先提公因式
二套
根据多项式的项数判断能否套用公式
若是二项式,则看是否符合平方差公式的特征
若是三项式,则看是否符合完全平方公式的特征
三检查
因式分解的结果一定要彻底,分解到每一个因式都不能再分解为止
例3 分解因式:
(1)-9a2+18ab-9b2;
(2)16a2(x-y)+b2(y-x).
例3 分解因式:
(1)-9a2+18ab-9b2;
(2)16a2(x-y)+b2(y-x).
分析 (1)先提取公因式,再利用完全平方公式分解因式即可;
(2)先提取公因式,再利用平方差公式分解因式即可.
例3 分解因式:
(1)-9a2+18ab-9b2;
(2)16a2(x-y)+b2(y-x).
分析 (1)先提取公因式,再利用完全平方公式分解因式即可;
(2)先提取公因式,再利用平方差公式分解因式即可.
解析 (1)原式=-9(a2-2ab+b2)=-9(a-b)2.
(2)原式=(x-y)(16a2-b2)=(x-y)(4a+b)(4a-b).
例3 分解因式:
(1)-9a2+18ab-9b2;
(2)16a2(x-y)+b2(y-x).
分析 (1)先提取公因式,再利用完全平方公式分解因式即可;
(2)先提取公因式,再利用平方差公式分解因式即可.
解析 (1)原式=-9(a2-2ab+b2)=-9(a-b)2.
(2)原式=(x-y)(16a2-b2)=(x-y)(4a+b)(4a-b).
点拨 综合应用各种方法分解因式时一定要注意分解是否彻底.
经典例题
题型一 综合运用公式法分解因式
例1 分解因式:
(1)(x2+4x)2-16; (2)a4-2a2b2+b4.
题型一 综合运用公式法分解因式
例1 分解因式:
(1)(x2+4x)2-16; (2)a4-2a2b2+b4.
解析 (1)原式=(x2+4x+4)(x2+4x-4)=(x+2)2(x2+4x-4).
(2)原式=(a2-b2)2=[(a+b)(a-b)]2=(a+b)2(a-b)2.
题型一 综合运用公式法分解因式
例1 分解因式:
(1)(x2+4x)2-16; (2)a4-2a2b2+b4.
解析 (1)原式=(x2+4x+4)(x2+4x-4)=(x+2)2(x2+4x-4).
(2)原式=(a2-b2)2=[(a+b)(a-b)]2=(a+b)2(a-b)2.
点拨 (1)当多项式的各项没有公因式时,一定要观察多项式的项数,如果多项式是二项式,那么应考虑是否具备平方差公式的特点,如果多项式是三项式,那么应考虑是否具备完全平方公式的特点.(2)当分解出来的因式还可以继续分解时,要继续分解,直至分解彻底.
题型二 求与完全平方式有关的字母参数的值
例2 若x2+(m-3)x+4是完全平方式,求m的值.
题型二 求与完全平方式有关的字母参数的值
例2 若x2+(m-3)x+4是完全平方式,求m的值.
分析 完全平方式是一个三项式,其中有两项能写成两个数(或式子)的平方的形式,且符号相同,第三项为这两个数(或式子)的积的2倍或-2倍.
题型二 求与完全平方式有关的字母参数的值
例2 若x2+(m-3)x+4是完全平方式,求m的值.
分析 完全平方式是一个三项式,其中有两项能写成两个数(或式子)的平方的形式,且符号相同,第三项为这两个数(或式子)的积的2倍或-2倍.
解析 因为x2+(m-3)x+4=x2+(m-3)x+22是完全平方式,所以(m-3)x=±2x×2=±4x,
所以m-3=±4,所以m=7或m=-1.
题型二 求与完全平方式有关的字母参数的值
例2 若x2+(m-3)x+4是完全平方式,求m的值.
分析 完全平方式是一个三项式,其中有两项能写成两个数(或式子)的平方的形式,且符号相同,第三项为这两个数(或式子)的积的2倍或-2倍.
解析 因为x2+(m-3)x+4=x2+(m-3)x+22是完全平方式,所以(m-3)x=±2x×2=±4x,
所以m-3=±4,所以m=7或m=-1.
点拨 在求与完全平方式有关的字母参数的值时,要注意“2倍乘积项”的符号有“+”“-”两种情况,不要漏解.
题型三 因式分解在几何问题中的应用
例3 已知a,b,c是△ABC的三边长,且满足a2-b2+ac+bc=0,试判断△ABC的形状.
题型三 因式分解在几何问题中的应用
例3 已知a,b,c是△ABC的三边长,且满足a2-b2+ac+bc=0,试判断△ABC的形状.
分析 由a,b,c是△ABC的三边长,知a>0,b>0,c>0,通过分解因式将方程左边变形,即可判断三角形的形状.
题型三 因式分解在几何问题中的应用
例3 已知a,b,c是△ABC的三边长,且满足a2-b2+ac+bc=0,试判断△ABC的形状.
分析 由a,b,c是△ABC的三边长,知a>0,b>0,c>0,通过分解因式将方程左边变形,即可判断三角形的形状.
解析 a2-b2+ac-bc=0,(a+b)(a-b)+(a-b)c=0,(a-b)(a+b+c)=0,
因为a,b,c是△ABC的三边长,所以a>0,b>0,c>0,所以a+b+c≠0,
所以a-b=0,即a=b,所以△ABC是等腰三角形.
易错易混
易错点 因式分解不彻底
例 因式分解:16x4-72x2+81.
易错点 因式分解不彻底
例 因式分解:16x4-72x2+81.
分析 先根据完全平方公式进行因式分解,再根据平方差公式进行因式分解.
易错点 因式分解不彻底
例 因式分解:16x4-72x2+81.
分析 先根据完全平方公式进行因式分解,再根据平方差公式进行因式分解.
解析 16x4-72x2+81=(4x2-9)2=(2x+3)2(2x-3)2.
易错点 因式分解不彻底
例 因式分解:16x4-72x2+81.
分析 先根据完全平方公式进行因式分解,再根据平方差公式进行因式分解.
解析 16x4-72x2+81=(4x2-9)2=(2x+3)2(2x-3)2.
易错警示 对于某些复杂的多项式,可能要多次用到公式法进行因式分解才能分解彻底,因此分解因式后一定要看式子是否还能继续分解.
3 公式法
知识点一 用平方差公式分解因式
法则
字母表示
举例
平方差公式
两个数的平方差,等于这两个数的和与这两个数的差的积
a2-b2=(a+b)(a-b)
4m2-9=(2m+3)(2m-3)
知识详解
(1)特点:等号左边是二项式,两项都是平方项,两项的符号相反;等号右边是两平方项的底数的和与底数的差的乘积.
(2)分解因式的时候,有公因式的先提公因式,提公因式后,如果剩下的多项式恰好可以表示成两项平方差的形式,那么就考虑运用平方差公式继续分解因式.
(3)公式中的a,b可以是单项式,也可以是多项式.
例1 把下列各式分解因式:
(1)-4m2+25n2;
(2)169(a+b)2-121(a-b)2.
例1 把下列各式分解因式:
(1)-4m2+25n2;
(2)169(a+b)2-121(a-b)2.
分析 (1)中的多项式可变为-(4m2-25n2),可写成-[(2m)2-(5n)2],从而利用平方差公式进行因式分解;(2)中的多项式可写成[13(a+b)]2-[11(a-b)]2,从而利用平方差公式进行因式分解.
解析 (1)-4m2+25n2
=-(4m2-25n2)
=-[(2m)2-(5n)2]
=-(2m+5n)(2m-5n)
(2)169(a+b)2-121(a-b)2
=[13(a+b)]2-[11(a-b)]2
=[13(a+b)+11(a-b)][13(a+b)-11(a-b)]
=(24a+2b)(2a+24b)
=4(12a+b)(a+12b)
解析 (1)-4m2+25n2
=-(4m2-25n2)
=-[(2m)2-(5n)2]
=-(2m+5n)(2m-5n)
(2)169(a+b)2-121(a-b)2
=[13(a+b)]2-[11(a-b)]2
=[13(a+b)+11(a-b)][13(a+b)-11(a-b)]
=(24a+2b)(2a+24b)
=4(12a+b)(a+12b)
点拨 运用平方差公式进行因式分解时,把多项式化成“平方差”的形式,以便明确哪项是公式中的a,哪项是公式中的b.
知识点二 用完全平方公式分解因式
1.完全平方公式
法则
字母表示
举例
完全平方公式
两个数(或式子)的平方和加上(或减去)这两个数(或式子)的积的2倍,等于这两个数(或式子)的和(或差)的平方
a2+2ab+b2=(a+b)2,a2-2ab+b2=(a-b)2
x2+4xy+4y2=(x+2y)2,x2-4xy+4y2=(x-2y)2
知识详解
(1)特点:等号左边是三项式,其中首尾两项分别是一个数(或式子)的平方,且这两项的符号相同,中间一项是这两个数(或式子)的积的2倍,符号正负均可;等号右边是这两个数(或式子)的和(或差)的平方.
(2)公式中的a,b可以是单项式,也可以是多项式.
2.公式法
通常我们把运用乘法公式进行因式分解的方法叫做公式法.
例2 分解因式:
(1)m2+14m+49;
(2)9x2-12x+4;
(3)a2+2a(b+c)+(b+c)2.
例2 分解因式:
(1)m2+14m+49;
(2)9x2-12x+4;
(3)a2+2a(b+c)+(b+c)2.
分析 (1)两个平方项是m2和72,可以用完全平方公式分解因式;(2)两个平方项分别为(3x)2和22,可以用完全平方公式分解因式;(3)两个平方项分别为a2和(b+c)2,可以用完全平方公式分解因式.
解析 (1)m2+14m+49=m2+2m×7+72=(m+7)2;(2)9x2-12x+4=(3x)2-2×3x×2+22=(3x-2)2;
(3)a2+2a(b+c)+(b+c)2=[a+(b+c)]2=(a+b+c)2.
解析 (1)m2+14m+49=m2+2m×7+72=(m+7)2;(2)9x2-12x+4=(3x)2-2×3x×2+22=(3x-2)2;
(3)a2+2a(b+c)+(b+c)2=[a+(b+c)]2=(a+b+c)2.
点拨 一个多项式可以利用完全平方公式分解因式时,这个多项式必须具备:(1)是一个三项式;(2)三项中有两项是两个数(或式子)的平方,第三项是这两个数(或式子)乘积的2倍或-2倍只有同时具备以上两个条件,才能用完全平方公式分解因式.
知识点三 综合应用各种方法分解因式
因为多项式的形式多种多样,所以因式分解的方法也有多种要迅速选择恰当的方法,必须注意从多项式的项数、各项符号、各项之间的关系等方面综合分析一般可遵循下列步骤进行:
知识点三 综合应用各种方法分解因式
因为多项式的形式多种多样,所以因式分解的方法也有多种要迅速选择恰当的方法,必须注意从多项式的项数、各项符号、各项之间的关系等方面综合分析一般可遵循下列步骤进行:
一提
看多项式的各项是否有公因式,若有,则应先提公因式
二套
根据多项式的项数判断能否套用公式
若是二项式,则看是否符合平方差公式的特征
若是三项式,则看是否符合完全平方公式的特征
三检查
因式分解的结果一定要彻底,分解到每一个因式都不能再分解为止
例3 分解因式:
(1)-9a2+18ab-9b2;
(2)16a2(x-y)+b2(y-x).
例3 分解因式:
(1)-9a2+18ab-9b2;
(2)16a2(x-y)+b2(y-x).
分析 (1)先提取公因式,再利用完全平方公式分解因式即可;
(2)先提取公因式,再利用平方差公式分解因式即可.
例3 分解因式:
(1)-9a2+18ab-9b2;
(2)16a2(x-y)+b2(y-x).
分析 (1)先提取公因式,再利用完全平方公式分解因式即可;
(2)先提取公因式,再利用平方差公式分解因式即可.
解析 (1)原式=-9(a2-2ab+b2)=-9(a-b)2.
(2)原式=(x-y)(16a2-b2)=(x-y)(4a+b)(4a-b).
例3 分解因式:
(1)-9a2+18ab-9b2;
(2)16a2(x-y)+b2(y-x).
分析 (1)先提取公因式,再利用完全平方公式分解因式即可;
(2)先提取公因式,再利用平方差公式分解因式即可.
解析 (1)原式=-9(a2-2ab+b2)=-9(a-b)2.
(2)原式=(x-y)(16a2-b2)=(x-y)(4a+b)(4a-b).
点拨 综合应用各种方法分解因式时一定要注意分解是否彻底.
经典例题
题型一 综合运用公式法分解因式
例1 分解因式:
(1)(x2+4x)2-16; (2)a4-2a2b2+b4.
题型一 综合运用公式法分解因式
例1 分解因式:
(1)(x2+4x)2-16; (2)a4-2a2b2+b4.
解析 (1)原式=(x2+4x+4)(x2+4x-4)=(x+2)2(x2+4x-4).
(2)原式=(a2-b2)2=[(a+b)(a-b)]2=(a+b)2(a-b)2.
题型一 综合运用公式法分解因式
例1 分解因式:
(1)(x2+4x)2-16; (2)a4-2a2b2+b4.
解析 (1)原式=(x2+4x+4)(x2+4x-4)=(x+2)2(x2+4x-4).
(2)原式=(a2-b2)2=[(a+b)(a-b)]2=(a+b)2(a-b)2.
点拨 (1)当多项式的各项没有公因式时,一定要观察多项式的项数,如果多项式是二项式,那么应考虑是否具备平方差公式的特点,如果多项式是三项式,那么应考虑是否具备完全平方公式的特点.(2)当分解出来的因式还可以继续分解时,要继续分解,直至分解彻底.
题型二 求与完全平方式有关的字母参数的值
例2 若x2+(m-3)x+4是完全平方式,求m的值.
题型二 求与完全平方式有关的字母参数的值
例2 若x2+(m-3)x+4是完全平方式,求m的值.
分析 完全平方式是一个三项式,其中有两项能写成两个数(或式子)的平方的形式,且符号相同,第三项为这两个数(或式子)的积的2倍或-2倍.
题型二 求与完全平方式有关的字母参数的值
例2 若x2+(m-3)x+4是完全平方式,求m的值.
分析 完全平方式是一个三项式,其中有两项能写成两个数(或式子)的平方的形式,且符号相同,第三项为这两个数(或式子)的积的2倍或-2倍.
解析 因为x2+(m-3)x+4=x2+(m-3)x+22是完全平方式,所以(m-3)x=±2x×2=±4x,
所以m-3=±4,所以m=7或m=-1.
题型二 求与完全平方式有关的字母参数的值
例2 若x2+(m-3)x+4是完全平方式,求m的值.
分析 完全平方式是一个三项式,其中有两项能写成两个数(或式子)的平方的形式,且符号相同,第三项为这两个数(或式子)的积的2倍或-2倍.
解析 因为x2+(m-3)x+4=x2+(m-3)x+22是完全平方式,所以(m-3)x=±2x×2=±4x,
所以m-3=±4,所以m=7或m=-1.
点拨 在求与完全平方式有关的字母参数的值时,要注意“2倍乘积项”的符号有“+”“-”两种情况,不要漏解.
题型三 因式分解在几何问题中的应用
例3 已知a,b,c是△ABC的三边长,且满足a2-b2+ac+bc=0,试判断△ABC的形状.
题型三 因式分解在几何问题中的应用
例3 已知a,b,c是△ABC的三边长,且满足a2-b2+ac+bc=0,试判断△ABC的形状.
分析 由a,b,c是△ABC的三边长,知a>0,b>0,c>0,通过分解因式将方程左边变形,即可判断三角形的形状.
题型三 因式分解在几何问题中的应用
例3 已知a,b,c是△ABC的三边长,且满足a2-b2+ac+bc=0,试判断△ABC的形状.
分析 由a,b,c是△ABC的三边长,知a>0,b>0,c>0,通过分解因式将方程左边变形,即可判断三角形的形状.
解析 a2-b2+ac-bc=0,(a+b)(a-b)+(a-b)c=0,(a-b)(a+b+c)=0,
因为a,b,c是△ABC的三边长,所以a>0,b>0,c>0,所以a+b+c≠0,
所以a-b=0,即a=b,所以△ABC是等腰三角形.
易错易混
易错点 因式分解不彻底
例 因式分解:16x4-72x2+81.
易错点 因式分解不彻底
例 因式分解:16x4-72x2+81.
分析 先根据完全平方公式进行因式分解,再根据平方差公式进行因式分解.
易错点 因式分解不彻底
例 因式分解:16x4-72x2+81.
分析 先根据完全平方公式进行因式分解,再根据平方差公式进行因式分解.
解析 16x4-72x2+81=(4x2-9)2=(2x+3)2(2x-3)2.
易错点 因式分解不彻底
例 因式分解:16x4-72x2+81.
分析 先根据完全平方公式进行因式分解,再根据平方差公式进行因式分解.
解析 16x4-72x2+81=(4x2-9)2=(2x+3)2(2x-3)2.
易错警示 对于某些复杂的多项式,可能要多次用到公式法进行因式分解才能分解彻底,因此分解因式后一定要看式子是否还能继续分解.
