4.4.3 不同函数增长的差异教案-2020-2021学年高中数学人教A版(2019)必修第一册
文档属性
| 名称 | 4.4.3 不同函数增长的差异教案-2020-2021学年高中数学人教A版(2019)必修第一册 |  | |
| 格式 | docx | ||
| 文件大小 | 393.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 21:07:23 | ||
图片预览


文档简介
4.4.3
不同函数增长的差异
教案
(一)课时教学内容
对比分析一次函数、对数函数和指数函数增长的差异.
(二)课时教学目标
利用信息技术,通过列表法和图象法,探究不同函数增长速度的各自特点及差异,并总结其中的规律.
(三)教学重点与难点
重点:一次函数、对数函数和指数函数各自增长的特点.
难点:归纳总结出不同函数增长的差异.体会对比地研究多个函数的过程.
(四)教学支持条件分析
本课时中,学生要有计算器.教师要充分应用软件进行计算或者绘制函数图象.
(五)教学过程设计
引导语:在4.2.1的例2的第(1)小问中,进一步研究了这一节的问题1,比较了A,B两地旅游收入的长期变化情况,A地为一次函数的增长,B地为指数函数的增长,两种增长方式存在很大的差异.那么该如何研究一次函数、指数函数和对数函数增长的差异?
1.指数函数与一次函数的增长差异
问题5:选取适当的指数函数与一次函数,探索它们在区间[0,+∞)上的增长差异.你能描述一下指数函数增长的特点吗?
追问1:不妨以函数和y=2x为例,列出这两个函数的自变量与函数值的对应表,并在同一直角坐标系中画出它们的图象.通过观察图象,这两个函数的图象在位置上有什么关系?这说明了什么?
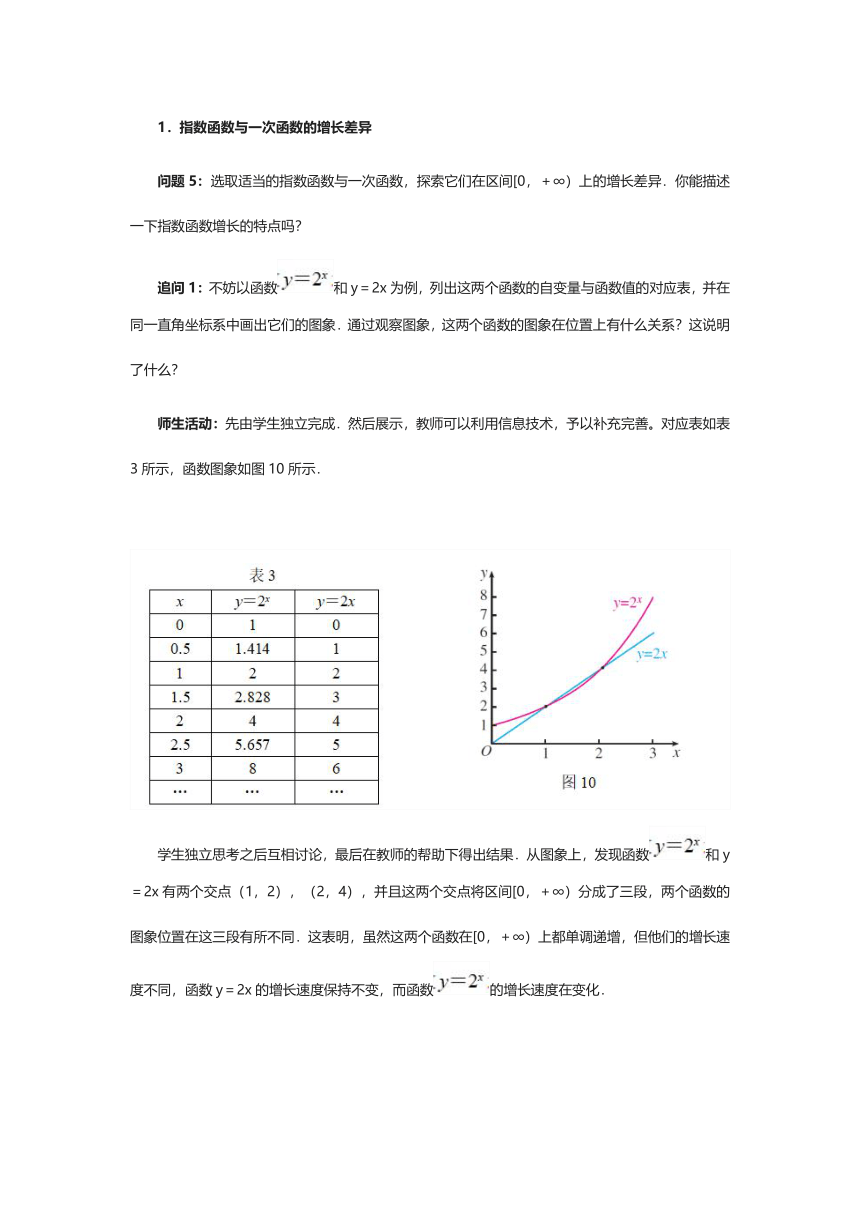
师生活动:先由学生独立完成.然后展示,教师可以利用信息技术,予以补充完善。对应表如表3所示,函数图象如图10所示.
学生独立思考之后互相讨论,最后在教师的帮助下得出结果.从图象上,发现函数和y=2x有两个交点(1,2),(2,4),并且这两个交点将区间[0,+∞)分成了三段,两个函数的图象位置在这三段有所不同.这表明,虽然这两个函数在[0,+∞)上都单调递增,但他们的增长速度不同,函数y=2x的增长速度保持不变,而函数的增长速度在变化.
??
追问3:在更大的范围内,列出这两个函数的自变量与函数值的对应表,并在同一直角坐标系中画出它们的图象,观察它们的增长情况,从图象上和数据上,你能发现什么?
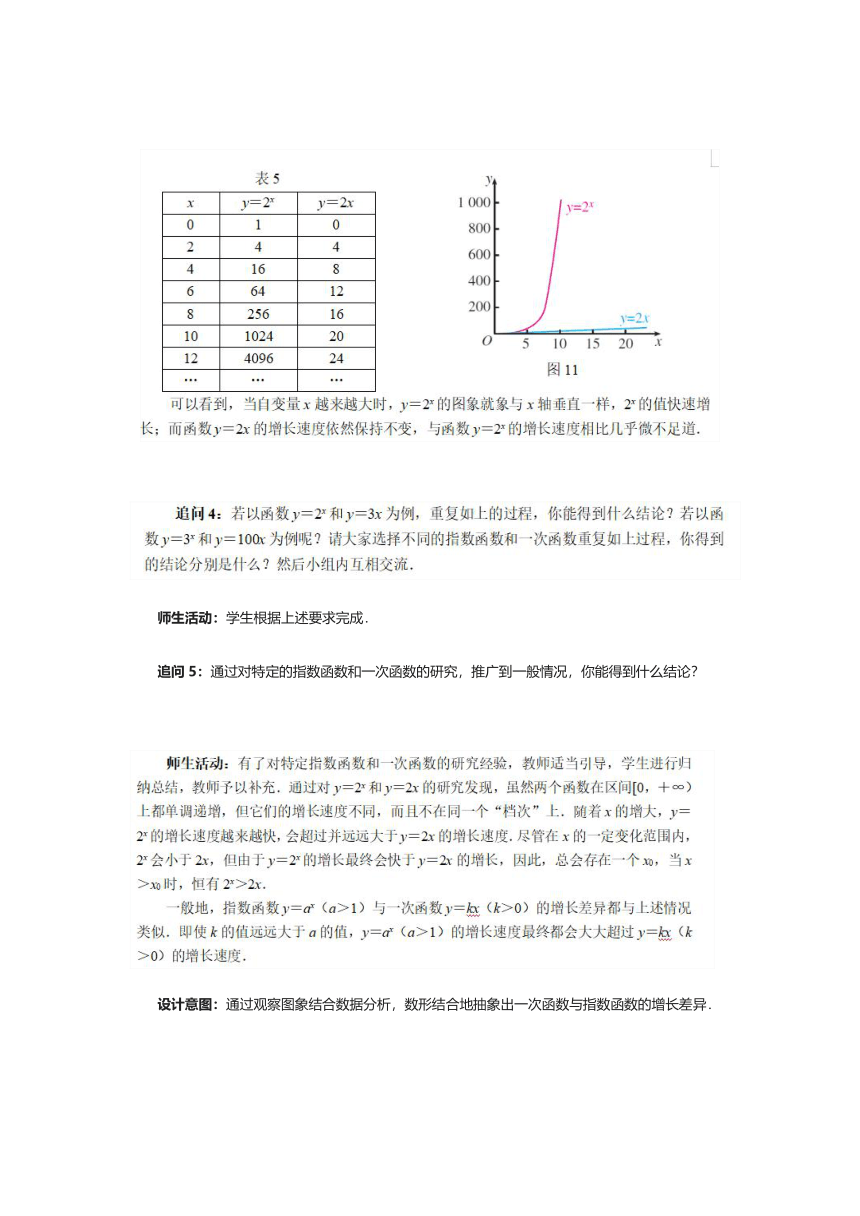
师生活动:有了前面的经验,借助计算工具和信息技术,教师引导并演示,全班集体完成即可.对应表如表5所示,函数图象如图11所示.
师生活动:学生根据上述要求完成.
追问5:通过对特定的指数函数和一次函数的研究,推广到一般情况,你能得到什么结论?
设计意图:通过观察图象结合数据分析,数形结合地抽象出一次函数与指数函数的增长差异.
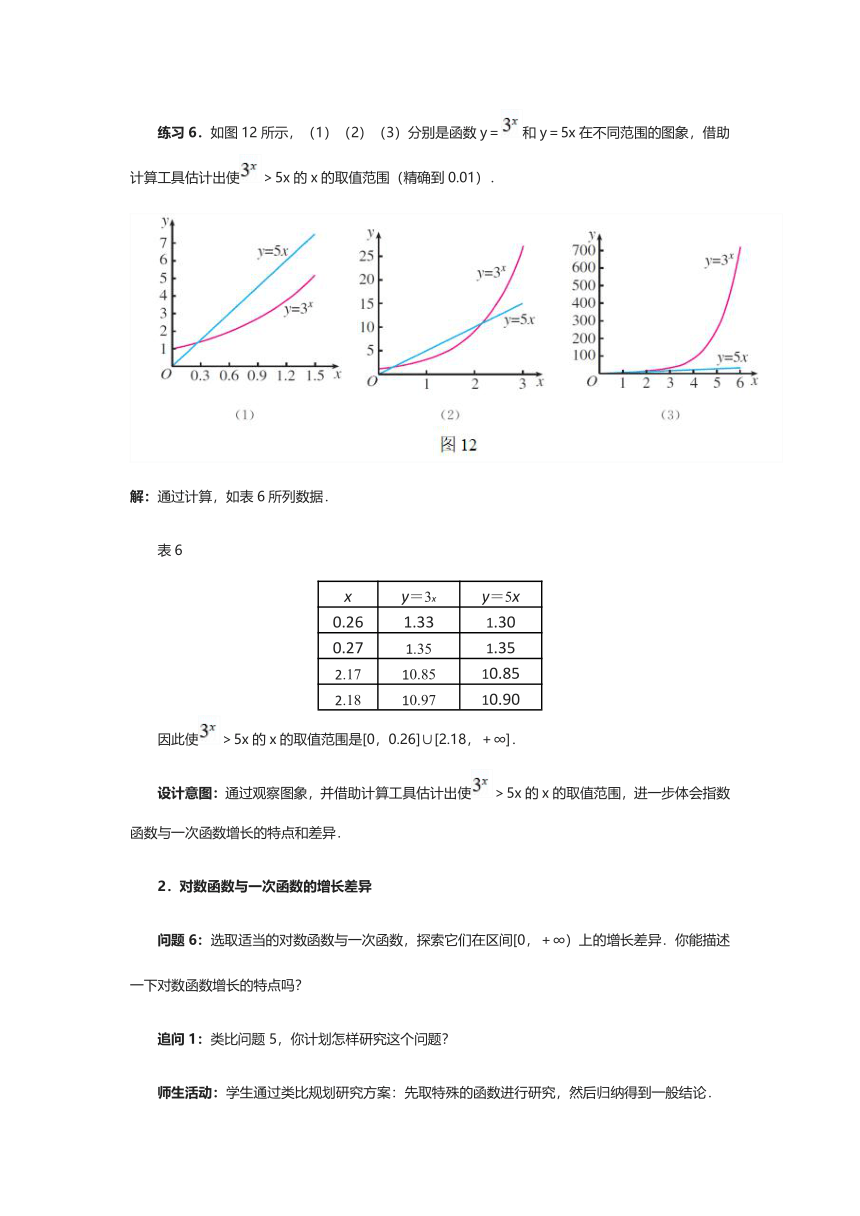
练习6.如图12所示,(1)(2)(3)分别是函数y=和y=5x在不同范围的图象,借助计算工具估计出使>5x的x的取值范围(精确到0.01).
解:通过计算,如表6所列数据.
表6
x
y=3x
y=5x
0.26
1.33
1.30
0.27
1.35
1.35
2.17
10.85
10.85
2.18
10.97
10.90
因此使>5x的x的取值范围是[0,0.26]∪[2.18,+∞].
设计意图:通过观察图象,并借助计算工具估计出使>5x的x的取值范围,进一步体会指数函数与一次函数增长的特点和差异.
2.对数函数与一次函数的增长差异
问题6:选取适当的对数函数与一次函数,探索它们在区间[0,+∞)上的增长差异.你能描述一下对数函数增长的特点吗?
追问1:类比问题5,你计划怎样研究这个问题?
师生活动:学生通过类比规划研究方案:先取特殊的函数进行研究,然后归纳得到一般结论.
追问2:既如此,不妨以函数y=lgx和为例,列出这两个函数的自变量与函数值的对应表,并在同一直角坐标系中画出它们的图象.
师生活动:先由学生独立完成,然后教师利用信息技术予以补充完善.对应表如表7所示,函数图象如图13所示.
追问3:通过观察图象,这两个函数的图象在位置上有什么关系?这说明了什么?
师生活动:教师提出问题,学生讨论得出结果.从图象上,发现函数y=lgx和虽然在[0,+∞)上都单调递增,但增长速度存在着明显的差异.随着x的增大,函数的图象离x轴越来越远,而函数y=lgx的图象越来越平缓,就象与x轴平行一样.
追问5:如果将lgx放大1000倍,再对函数y=1000lgx和的增长情况进行比较,那么仍然有前面所述的规律吗?
师生活动:有了前面的经验,教师引导学生进行定性分析.从图象和数据上都可以看出,随着x的增大,一次函数的增长速度保持不变,而对数函数的增长速度一直在减小.所以一定存在一个,当x>时,y=1000lgx的增长速度比的增长速度小,并且y=1000lgx的增长速度还会持续减小下去.
追问6:通过对特定的对数函数和一次函数的研究,推广到一般情况,你能得到什么结论?
师生活动:有了对特定对数函数和一次函数的研究经验,教师适当引导,学生进行归纳总结,教师予以补充.通过对y=lgx和的研究发现,虽然两个函数在区间[0,+∞)上都单调递增,但它们的增长速度不同,而且不在同一个“档次”上.随着x的增大,y=lgx的增长速度越来越慢,与的增长速度相比几乎微不足道.
设计意图:通过观察图象结合数据分析,数形结合地抽象出一次函数与对数函数的增长差异.
练习7.如图14,对数函数y=lgx的图象与一次函数y=f(x)的图象有A,B两个公共点.求一次函数y=f(x)的解析式.
?
解:根据对数函数的性质可知,y=lgx过定点(1,0),即A(1,0).又当x=2时,对数函数y=lg2,即B(2,lg2).因此过A,B两点的直线方程为y=lg2×(x-1),即一次函数y=f(x)的解析式为y=lg2×(x-1).
设计意图:通过观察图象,并根据对数函数与一次函数的性质,作定量计算,进一步体会对数函数与一次函数增长的特点和差异.
3.同时比较一次函数、对数函数和指数函数
问题7:在问题5和问题6中,分别研究了指数函数与一次函数、对数函数与一次函数的增长差异,如果将一次函数、对数函数和指数函数同时比较,你能得到什么结论?
师生活动:教师提出问题,引导学生借助信息技术画出图象进行探索.函数图象如图15所示.
?
追问2:一次函数y=kx(k>0),对数函数(a>1)和指数函数(b>1)的增长有何差异?
师生活动:有了前面的研究经验,教师适当引导,学生进行归纳总结,教师予以补充.一般地,无论k(k>0)、a(a>1)、b(b>1)取何值,三种函数在区间(0,+∞)上都单调递增,但一次函数总是保持固定的增长速度;对数函数的增长速度都会越来越慢,并且对数函数的函数值最终总会小于一次函数的函数值;指数函数的增长速度都会越来越快,并且指数函数的函数值最终总会大于一次函数的函数值.
追问3:如何理解“直线上升”“对数增长”“指数爆炸”的含义?
师生活动:“直线上升”“对数增长”“指数爆炸”从字面意义理解,直观形象、顾名思义,可充分发挥学生的积极性展开讨论.教师个别提问讨论的结果,只要学生正确理解即可,没有特定的标准答案.
设计意图:通过同时比较三种函数的增长差异,进一步认识一次函数、对数函数和指数函数的性质,体会它们之间增长的差异.
?
解:根据函数图象,该函数应该呈对数增长.结合函数的性质,该函数过(1,0),符合对数函数的特点.注意到当函数值y=1时,x的值大约在2到3之间,所以该对数函数的底数应该在2到3之间.因此y=f(x)可能是y=lnx,选C.
设计意图:通过列表法和图象法,进一步体会一次函数、对数函数和指数函数的增长差异.并应用这种差异,解决问题.
4.课时小结
教师引导学生回顾本课时学习内容,并回答下面问题:
(1)概述本节课研究一次函数、对数函数和指数函数增长的差异的基本过程.
(2)掌握不同函数增长的差异,有什么现实意义?
师生活动:提出问题后,先让学生思考并做适当交流,再让学生发言,教师帮助完善.
(1)本节课先从简单情况入手,先分别比较一次函数与指数函数、一次函数与对数函数,然后再将三个函数放在一起同时比较.在比较它们增长的差异时,先从特定情况研究,分别通过图象、数据分析计算它们增长的差异,然后再归纳出一般情况.
(2)掌握了不同函数增长的差异,就可以根据现实问题的增长情况,选择合适的函数模型刻画其变化规律.
设计意图:(1)在前面两个课时中,是针对一个函数的研究套路“背景-概念-图象与性质-应用”.本课时是同时研究多个函数的相关性,通过总结研究过程,使学生初步了解对比地研究多个相关对象的基本套路.
(2)了解不同函数增长的差异的现实意义,可以使学生更好地掌握一次函数、对数函数和指数函数之间的联系,以及它们的差异,并能够学以致用,达到知识技能的灵活应用.
5.布置作业
根据课堂教学情况,从教科书习题4.4中选择合适的题目.可选题目:第6,11题.
(六)目标检测设计
设计意图:考查学生是否掌握一次函数、对数函数和指数函数增长的差异,并能够应用增长差异和增长趋势,解决相关问题.
五、单元小结
教师引导学生回顾本单元学习的主要内容,并回答下列问题:
(1)写出一个对数函数的解析式,说明底数的值,画出该函数的草图,并说明其单调性和增长规律.
(2)通过本单元的学习,你对研究函数的内容和方法有什么更进一步的认识?对比以前学习过的一些具体函数,你能建立指数函数和它们的联系吗,请你结合表9谈谈体会.
表9
对数函数
指数函数
一次函数
二次函数
反比例函数
幂函数
解析式
?
?
?
?
?
?
定义域
?
?
?
?
?
?
值 域
?
?
?
?
?
?
图 象
?
?
?
?
?
?
性 质
?
?
?
?
?
?
增长趋势
?
?
?
?
?
师生活动:(1)该问题无固定答案,学生独立完成,教师单独提问,只要回答符合要求,合理正确即可.
(2)教师引导学生,可通过讨论完成.
设计意图:(1)教师与学生一起回顾本单元学习的对数函数的概念、图象和性质.
(2)建立对数函数与学习过的其它函数的联系,并进一步体会研究具体函数的内容、过程和方法.
不同函数增长的差异
教案
(一)课时教学内容
对比分析一次函数、对数函数和指数函数增长的差异.
(二)课时教学目标
利用信息技术,通过列表法和图象法,探究不同函数增长速度的各自特点及差异,并总结其中的规律.
(三)教学重点与难点
重点:一次函数、对数函数和指数函数各自增长的特点.
难点:归纳总结出不同函数增长的差异.体会对比地研究多个函数的过程.
(四)教学支持条件分析
本课时中,学生要有计算器.教师要充分应用软件进行计算或者绘制函数图象.
(五)教学过程设计
引导语:在4.2.1的例2的第(1)小问中,进一步研究了这一节的问题1,比较了A,B两地旅游收入的长期变化情况,A地为一次函数的增长,B地为指数函数的增长,两种增长方式存在很大的差异.那么该如何研究一次函数、指数函数和对数函数增长的差异?
1.指数函数与一次函数的增长差异
问题5:选取适当的指数函数与一次函数,探索它们在区间[0,+∞)上的增长差异.你能描述一下指数函数增长的特点吗?
追问1:不妨以函数和y=2x为例,列出这两个函数的自变量与函数值的对应表,并在同一直角坐标系中画出它们的图象.通过观察图象,这两个函数的图象在位置上有什么关系?这说明了什么?
师生活动:先由学生独立完成.然后展示,教师可以利用信息技术,予以补充完善。对应表如表3所示,函数图象如图10所示.
学生独立思考之后互相讨论,最后在教师的帮助下得出结果.从图象上,发现函数和y=2x有两个交点(1,2),(2,4),并且这两个交点将区间[0,+∞)分成了三段,两个函数的图象位置在这三段有所不同.这表明,虽然这两个函数在[0,+∞)上都单调递增,但他们的增长速度不同,函数y=2x的增长速度保持不变,而函数的增长速度在变化.
??
追问3:在更大的范围内,列出这两个函数的自变量与函数值的对应表,并在同一直角坐标系中画出它们的图象,观察它们的增长情况,从图象上和数据上,你能发现什么?
师生活动:有了前面的经验,借助计算工具和信息技术,教师引导并演示,全班集体完成即可.对应表如表5所示,函数图象如图11所示.
师生活动:学生根据上述要求完成.
追问5:通过对特定的指数函数和一次函数的研究,推广到一般情况,你能得到什么结论?
设计意图:通过观察图象结合数据分析,数形结合地抽象出一次函数与指数函数的增长差异.
练习6.如图12所示,(1)(2)(3)分别是函数y=和y=5x在不同范围的图象,借助计算工具估计出使>5x的x的取值范围(精确到0.01).
解:通过计算,如表6所列数据.
表6
x
y=3x
y=5x
0.26
1.33
1.30
0.27
1.35
1.35
2.17
10.85
10.85
2.18
10.97
10.90
因此使>5x的x的取值范围是[0,0.26]∪[2.18,+∞].
设计意图:通过观察图象,并借助计算工具估计出使>5x的x的取值范围,进一步体会指数函数与一次函数增长的特点和差异.
2.对数函数与一次函数的增长差异
问题6:选取适当的对数函数与一次函数,探索它们在区间[0,+∞)上的增长差异.你能描述一下对数函数增长的特点吗?
追问1:类比问题5,你计划怎样研究这个问题?
师生活动:学生通过类比规划研究方案:先取特殊的函数进行研究,然后归纳得到一般结论.
追问2:既如此,不妨以函数y=lgx和为例,列出这两个函数的自变量与函数值的对应表,并在同一直角坐标系中画出它们的图象.
师生活动:先由学生独立完成,然后教师利用信息技术予以补充完善.对应表如表7所示,函数图象如图13所示.
追问3:通过观察图象,这两个函数的图象在位置上有什么关系?这说明了什么?
师生活动:教师提出问题,学生讨论得出结果.从图象上,发现函数y=lgx和虽然在[0,+∞)上都单调递增,但增长速度存在着明显的差异.随着x的增大,函数的图象离x轴越来越远,而函数y=lgx的图象越来越平缓,就象与x轴平行一样.
追问5:如果将lgx放大1000倍,再对函数y=1000lgx和的增长情况进行比较,那么仍然有前面所述的规律吗?
师生活动:有了前面的经验,教师引导学生进行定性分析.从图象和数据上都可以看出,随着x的增大,一次函数的增长速度保持不变,而对数函数的增长速度一直在减小.所以一定存在一个,当x>时,y=1000lgx的增长速度比的增长速度小,并且y=1000lgx的增长速度还会持续减小下去.
追问6:通过对特定的对数函数和一次函数的研究,推广到一般情况,你能得到什么结论?
师生活动:有了对特定对数函数和一次函数的研究经验,教师适当引导,学生进行归纳总结,教师予以补充.通过对y=lgx和的研究发现,虽然两个函数在区间[0,+∞)上都单调递增,但它们的增长速度不同,而且不在同一个“档次”上.随着x的增大,y=lgx的增长速度越来越慢,与的增长速度相比几乎微不足道.
设计意图:通过观察图象结合数据分析,数形结合地抽象出一次函数与对数函数的增长差异.
练习7.如图14,对数函数y=lgx的图象与一次函数y=f(x)的图象有A,B两个公共点.求一次函数y=f(x)的解析式.
?
解:根据对数函数的性质可知,y=lgx过定点(1,0),即A(1,0).又当x=2时,对数函数y=lg2,即B(2,lg2).因此过A,B两点的直线方程为y=lg2×(x-1),即一次函数y=f(x)的解析式为y=lg2×(x-1).
设计意图:通过观察图象,并根据对数函数与一次函数的性质,作定量计算,进一步体会对数函数与一次函数增长的特点和差异.
3.同时比较一次函数、对数函数和指数函数
问题7:在问题5和问题6中,分别研究了指数函数与一次函数、对数函数与一次函数的增长差异,如果将一次函数、对数函数和指数函数同时比较,你能得到什么结论?
师生活动:教师提出问题,引导学生借助信息技术画出图象进行探索.函数图象如图15所示.
?
追问2:一次函数y=kx(k>0),对数函数(a>1)和指数函数(b>1)的增长有何差异?
师生活动:有了前面的研究经验,教师适当引导,学生进行归纳总结,教师予以补充.一般地,无论k(k>0)、a(a>1)、b(b>1)取何值,三种函数在区间(0,+∞)上都单调递增,但一次函数总是保持固定的增长速度;对数函数的增长速度都会越来越慢,并且对数函数的函数值最终总会小于一次函数的函数值;指数函数的增长速度都会越来越快,并且指数函数的函数值最终总会大于一次函数的函数值.
追问3:如何理解“直线上升”“对数增长”“指数爆炸”的含义?
师生活动:“直线上升”“对数增长”“指数爆炸”从字面意义理解,直观形象、顾名思义,可充分发挥学生的积极性展开讨论.教师个别提问讨论的结果,只要学生正确理解即可,没有特定的标准答案.
设计意图:通过同时比较三种函数的增长差异,进一步认识一次函数、对数函数和指数函数的性质,体会它们之间增长的差异.
?
解:根据函数图象,该函数应该呈对数增长.结合函数的性质,该函数过(1,0),符合对数函数的特点.注意到当函数值y=1时,x的值大约在2到3之间,所以该对数函数的底数应该在2到3之间.因此y=f(x)可能是y=lnx,选C.
设计意图:通过列表法和图象法,进一步体会一次函数、对数函数和指数函数的增长差异.并应用这种差异,解决问题.
4.课时小结
教师引导学生回顾本课时学习内容,并回答下面问题:
(1)概述本节课研究一次函数、对数函数和指数函数增长的差异的基本过程.
(2)掌握不同函数增长的差异,有什么现实意义?
师生活动:提出问题后,先让学生思考并做适当交流,再让学生发言,教师帮助完善.
(1)本节课先从简单情况入手,先分别比较一次函数与指数函数、一次函数与对数函数,然后再将三个函数放在一起同时比较.在比较它们增长的差异时,先从特定情况研究,分别通过图象、数据分析计算它们增长的差异,然后再归纳出一般情况.
(2)掌握了不同函数增长的差异,就可以根据现实问题的增长情况,选择合适的函数模型刻画其变化规律.
设计意图:(1)在前面两个课时中,是针对一个函数的研究套路“背景-概念-图象与性质-应用”.本课时是同时研究多个函数的相关性,通过总结研究过程,使学生初步了解对比地研究多个相关对象的基本套路.
(2)了解不同函数增长的差异的现实意义,可以使学生更好地掌握一次函数、对数函数和指数函数之间的联系,以及它们的差异,并能够学以致用,达到知识技能的灵活应用.
5.布置作业
根据课堂教学情况,从教科书习题4.4中选择合适的题目.可选题目:第6,11题.
(六)目标检测设计
设计意图:考查学生是否掌握一次函数、对数函数和指数函数增长的差异,并能够应用增长差异和增长趋势,解决相关问题.
五、单元小结
教师引导学生回顾本单元学习的主要内容,并回答下列问题:
(1)写出一个对数函数的解析式,说明底数的值,画出该函数的草图,并说明其单调性和增长规律.
(2)通过本单元的学习,你对研究函数的内容和方法有什么更进一步的认识?对比以前学习过的一些具体函数,你能建立指数函数和它们的联系吗,请你结合表9谈谈体会.
表9
对数函数
指数函数
一次函数
二次函数
反比例函数
幂函数
解析式
?
?
?
?
?
?
定义域
?
?
?
?
?
?
值 域
?
?
?
?
?
?
图 象
?
?
?
?
?
?
性 质
?
?
?
?
?
?
增长趋势
?
?
?
?
?
师生活动:(1)该问题无固定答案,学生独立完成,教师单独提问,只要回答符合要求,合理正确即可.
(2)教师引导学生,可通过讨论完成.
设计意图:(1)教师与学生一起回顾本单元学习的对数函数的概念、图象和性质.
(2)建立对数函数与学习过的其它函数的联系,并进一步体会研究具体函数的内容、过程和方法.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
