中心对称图形课件
图片预览








文档简介
(共39张PPT)
下面图1的扑克牌中,把其中一张旋转180°后,得到下图2,聪明的你能找到旋转的是哪一张牌吗?
小游戏:
图一
图二
第15章 平移与旋转
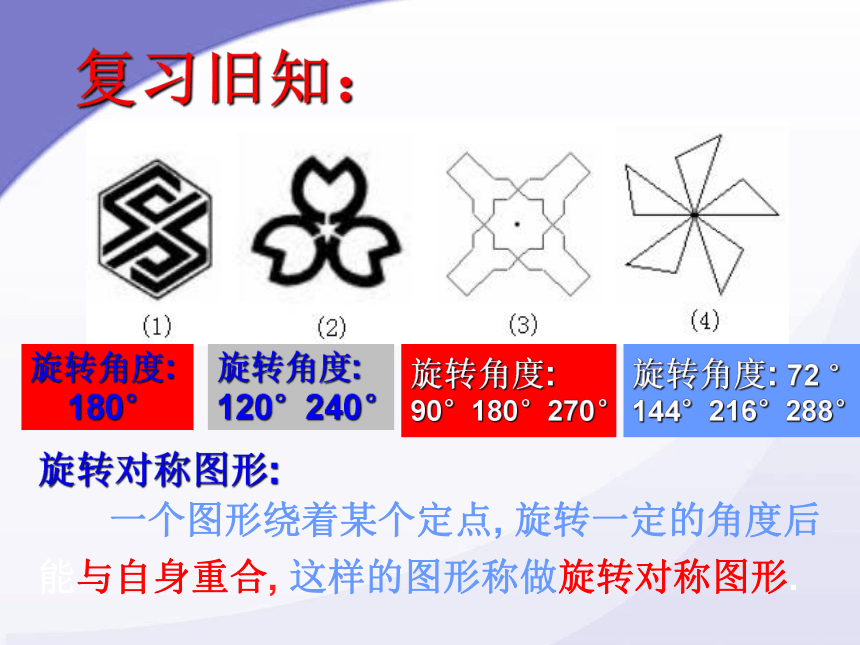
旋转对称图形:
一个图形绕着某个定点, 旋转一定的角度后
能与自身重合, 这样的图形称做旋转对称图形.
旋转角度:
120°240°
旋转角度:
180°
旋转角度:
90°180°270°
旋转角度: 72 °
144°216°288°
复习旧知:
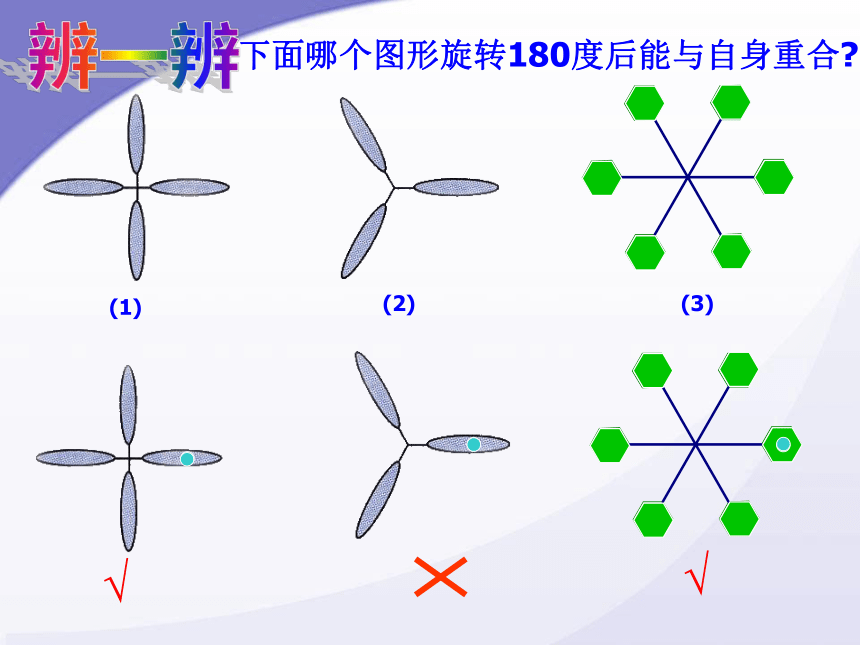
下面哪个图形旋转180度后能与自身重合
(1)
(3)
(2)
√
√
在我们周围还有哪些图形和这些图形一样旋转180°后能和自己完全重合???
想一想
走进生活
你还能举出生活中应用旋转对称的例子吗?
动脑搜一搜。。。
禁止车辆长时间停放
禁止车辆临时或长时间停放
数学走进生活
奥迪
现代
新知导航:
中心对称图形
旋转对称图形
一个图形绕着某个定点, 旋转 能与自身重合, 这样的图形称做 。这个点叫做 。
中心对称图形是旋转角度为180°的旋转对称图形
180°
中心对称图形
对称中心
一定角度
旋转对称图形
旋转中心
旋转角度为180°
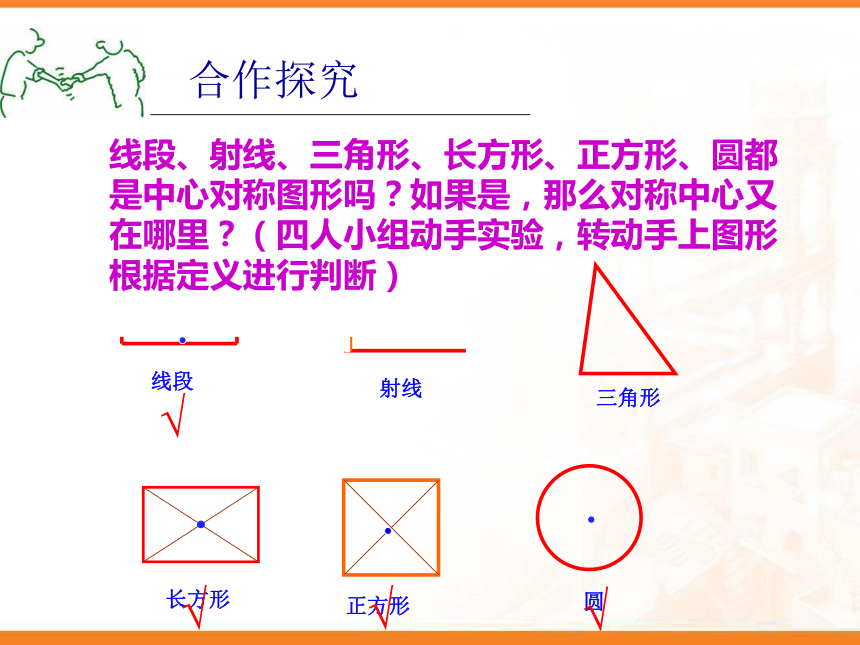
线段、射线、三角形、长方形、正方形、圆都是中心对称图形吗?如果是,那么对称中心又在哪里?(四人小组动手实验,转动手上图形根据定义进行判断)
正方形
三角形
长方形
圆
线段
射线
√
√
√
√
合作探究
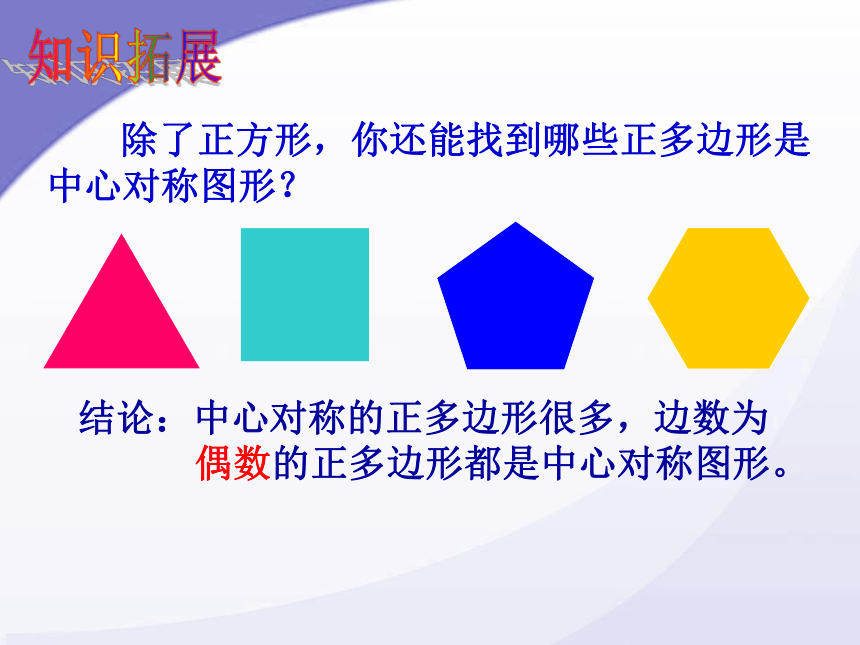
除了正方形,你还能找到哪些正多边形是
中心对称图形?
结论:中心对称的正多边形很多,边数为
偶数的正多边形都是中心对称图形。
世界上因为有了圆的图案,万物才显得富有生机,以下来自现实生活的图形中都有圆,它们看上去是那么美丽与和谐,这正是因为圆具有轴对称和中心对称性。
请问以下三个图形中是轴对称图形的有 ,是中心对称图形的有 。
一石激起千层浪
汽车方向盘
铜钱
(1)
(2)
(3)
(1)(2)(3)
(1)(3)
看一看
以下五家银行行标中,既是中心对称图形又是轴对称图形的有( )
1、中国文字丰富多彩、含义深刻,有许多是
中心对称的,比如口、日等,你还能找出几个
个吗?
2、以下五家银行行标中,既是中心对称图形又是轴对称图形的有____个
√
√
2
以下图形中是轴对称图形的有_____________
是旋转对称图形的有__________________________
是中心对称图形的有_______________________
(1)
(2)
(3)
(5)
(6)
(7)
(8)
(4)
1、2、3、5、6
1、3、4、5、7、8
1、3、4、5、7
中心对称图形:
H、I、N、O、S、X、Z
(1)把其中一个图案绕点O旋转180°.你有什么发现
重 合
重 合
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°.你有什么发现
O
A
O
D
B
C
观察分析,
探究新知
你能说说这两个图形的变换有什么共同的特征吗?
1.中心对称图形的定义:
把一个图形绕着一个点旋转180 后,能与自身重合,那么就说这一个图形是中心对称图形。
2.中心对称的定义
把一个图形绕着一个点旋转180 ,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称。
中心对称:
把一个图形绕着某一点旋转180 ,如果它能够与另一个图形重合,那么就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点。
练习:△ABC与△ADE是成中心对称的两个三角形,点A是对称中心,请分别找出图中的对称点和相等的线段。
初步运用
巩固基础
中心对称
轴对称
中心对称与轴对称有什么区别 又有什么联系
A
B
C
A
B
C
旋转三角板,画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;
A’
B’
C’
O
A
B
C
第三步,移开三角板.
合作探究:
合作探究:
旋转三角板,画关于点O对称的两个三角形:
分别连接AA’、BB’,CC’。
点O在线段AA′上吗?
如果在,在什么位置? △ABC与△A′B′C′有什么关系?
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;
O
A’
B’
C’
C
B
A
很显然画出的△ABC与△A’B’C’关于点O对称.
第三步,移开三角板.
如图,△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系
探索
我们可以发现,点A绕中心点O旋转180°后到点A′,于是A、 O、 A′三点在一直线上,
并且AO=OA′,另外分别在一直线上的三点还有 、 ;
并且BO= , CO=
尝试归纳:关于中心对称的两个图形有哪些性质?
2、反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称。
1、在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分。
归纳:
例2.如图所示的两个图形成中心对称,你能找到对称点吗?如何找到对称中心?
两对对称点连线的交点
巩固练习:如图,两个图形关于某点成中心对称,看谁能用最简单的方法找出对称中心。你的根据是什么?
游戏规则:每位同学都作为平面内的一个点,挑选三位同学参加游戏,
(1)C同学作为对称中心,大家一起找同学A的朋友B;
(2)A和B是关于C的对称点,大家一起找对称中心C。如果B同学能在大家发现之前站起来,B就是游戏的胜利者;
名称 中心对称 中心对称图形
定义
联系
把一个图形绕着某一个点旋转180 ,如果它能够与另一个图形重合,那么就说这两个图形成中心对称,两个图形关于点对称也称中心对称
如果一个图形绕着一个点旋转180 后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形
若把中心对称图形的两部分分别看作两个图形,
则它们成中心对称
若把中心对称的两个图形看作一个整体,则成为
中心对称图形。
请你来总结
请以给定的图形○○△△=(两个圆,两个三角形,两条平行线)为构件,尽可能多地构思有意义的一些中心图形,并写上一两句贴切,诙谐的解说词.如下图就是符合要求的图形,你能构思其它图形吗 比一比,看谁想得多,看谁想得妙!
拓展提高:
路灯与倒影
指南针
除号
沙漏
两只拔河的小鸡
想 一 想
1、本节课学到了哪些知识?
(1)中心对称图形和中心对称的概念
(2)中心对称的性质
(3)了解了中心对称图形和中心对
称的区别和联系
课堂小结:
(4)认识了中心对称图形的应用
2、走进数学——
我们会发觉生活中处处都有她的身影;
会发现许多令人惊喜的东西;
我们还会感到自己变得越来越聪明、
越来越有本领。
许多以前不会解决的问题、不会做的事情,
现在都能干得很好了!
让我们走进数学,热爱数学,享受数学!
课堂小考
下面图1的扑克牌中,把其中一张旋转180°后,得到下图2,聪明的你能找到旋转的是哪一张牌吗?
小游戏:
图一
图二
第15章 平移与旋转
旋转对称图形:
一个图形绕着某个定点, 旋转一定的角度后
能与自身重合, 这样的图形称做旋转对称图形.
旋转角度:
120°240°
旋转角度:
180°
旋转角度:
90°180°270°
旋转角度: 72 °
144°216°288°
复习旧知:
下面哪个图形旋转180度后能与自身重合
(1)
(3)
(2)
√
√
在我们周围还有哪些图形和这些图形一样旋转180°后能和自己完全重合???
想一想
走进生活
你还能举出生活中应用旋转对称的例子吗?
动脑搜一搜。。。
禁止车辆长时间停放
禁止车辆临时或长时间停放
数学走进生活
奥迪
现代
新知导航:
中心对称图形
旋转对称图形
一个图形绕着某个定点, 旋转 能与自身重合, 这样的图形称做 。这个点叫做 。
中心对称图形是旋转角度为180°的旋转对称图形
180°
中心对称图形
对称中心
一定角度
旋转对称图形
旋转中心
旋转角度为180°
线段、射线、三角形、长方形、正方形、圆都是中心对称图形吗?如果是,那么对称中心又在哪里?(四人小组动手实验,转动手上图形根据定义进行判断)
正方形
三角形
长方形
圆
线段
射线
√
√
√
√
合作探究
除了正方形,你还能找到哪些正多边形是
中心对称图形?
结论:中心对称的正多边形很多,边数为
偶数的正多边形都是中心对称图形。
世界上因为有了圆的图案,万物才显得富有生机,以下来自现实生活的图形中都有圆,它们看上去是那么美丽与和谐,这正是因为圆具有轴对称和中心对称性。
请问以下三个图形中是轴对称图形的有 ,是中心对称图形的有 。
一石激起千层浪
汽车方向盘
铜钱
(1)
(2)
(3)
(1)(2)(3)
(1)(3)
看一看
以下五家银行行标中,既是中心对称图形又是轴对称图形的有( )
1、中国文字丰富多彩、含义深刻,有许多是
中心对称的,比如口、日等,你还能找出几个
个吗?
2、以下五家银行行标中,既是中心对称图形又是轴对称图形的有____个
√
√
2
以下图形中是轴对称图形的有_____________
是旋转对称图形的有__________________________
是中心对称图形的有_______________________
(1)
(2)
(3)
(5)
(6)
(7)
(8)
(4)
1、2、3、5、6
1、3、4、5、7、8
1、3、4、5、7
中心对称图形:
H、I、N、O、S、X、Z
(1)把其中一个图案绕点O旋转180°.你有什么发现
重 合
重 合
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°.你有什么发现
O
A
O
D
B
C
观察分析,
探究新知
你能说说这两个图形的变换有什么共同的特征吗?
1.中心对称图形的定义:
把一个图形绕着一个点旋转180 后,能与自身重合,那么就说这一个图形是中心对称图形。
2.中心对称的定义
把一个图形绕着一个点旋转180 ,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称。
中心对称:
把一个图形绕着某一点旋转180 ,如果它能够与另一个图形重合,那么就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点。
练习:△ABC与△ADE是成中心对称的两个三角形,点A是对称中心,请分别找出图中的对称点和相等的线段。
初步运用
巩固基础
中心对称
轴对称
中心对称与轴对称有什么区别 又有什么联系
A
B
C
A
B
C
旋转三角板,画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;
A’
B’
C’
O
A
B
C
第三步,移开三角板.
合作探究:
合作探究:
旋转三角板,画关于点O对称的两个三角形:
分别连接AA’、BB’,CC’。
点O在线段AA′上吗?
如果在,在什么位置? △ABC与△A′B′C′有什么关系?
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;
O
A’
B’
C’
C
B
A
很显然画出的△ABC与△A’B’C’关于点O对称.
第三步,移开三角板.
如图,△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系
探索
我们可以发现,点A绕中心点O旋转180°后到点A′,于是A、 O、 A′三点在一直线上,
并且AO=OA′,另外分别在一直线上的三点还有 、 ;
并且BO= , CO=
尝试归纳:关于中心对称的两个图形有哪些性质?
2、反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称。
1、在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分。
归纳:
例2.如图所示的两个图形成中心对称,你能找到对称点吗?如何找到对称中心?
两对对称点连线的交点
巩固练习:如图,两个图形关于某点成中心对称,看谁能用最简单的方法找出对称中心。你的根据是什么?
游戏规则:每位同学都作为平面内的一个点,挑选三位同学参加游戏,
(1)C同学作为对称中心,大家一起找同学A的朋友B;
(2)A和B是关于C的对称点,大家一起找对称中心C。如果B同学能在大家发现之前站起来,B就是游戏的胜利者;
名称 中心对称 中心对称图形
定义
联系
把一个图形绕着某一个点旋转180 ,如果它能够与另一个图形重合,那么就说这两个图形成中心对称,两个图形关于点对称也称中心对称
如果一个图形绕着一个点旋转180 后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形
若把中心对称图形的两部分分别看作两个图形,
则它们成中心对称
若把中心对称的两个图形看作一个整体,则成为
中心对称图形。
请你来总结
请以给定的图形○○△△=(两个圆,两个三角形,两条平行线)为构件,尽可能多地构思有意义的一些中心图形,并写上一两句贴切,诙谐的解说词.如下图就是符合要求的图形,你能构思其它图形吗 比一比,看谁想得多,看谁想得妙!
拓展提高:
路灯与倒影
指南针
除号
沙漏
两只拔河的小鸡
想 一 想
1、本节课学到了哪些知识?
(1)中心对称图形和中心对称的概念
(2)中心对称的性质
(3)了解了中心对称图形和中心对
称的区别和联系
课堂小结:
(4)认识了中心对称图形的应用
2、走进数学——
我们会发觉生活中处处都有她的身影;
会发现许多令人惊喜的东西;
我们还会感到自己变得越来越聪明、
越来越有本领。
许多以前不会解决的问题、不会做的事情,
现在都能干得很好了!
让我们走进数学,热爱数学,享受数学!
课堂小考
