六年级数学上册课件 3.6 比的认识 苏教版(30张ppt)
文档属性
| 名称 | 六年级数学上册课件 3.6 比的认识 苏教版(30张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 16:51:32 | ||
图片预览










文档简介
分数除法
第6课时 比的认识
1.使学生理解比的意义,会读、写比,认识比的各个部分名称;掌握求比值的方法,能准确地求出比值。 ? ?????
2.使学生理解比、分数、除法之间的联系与区别,通过观察和思考,理解数学知识之间是互相联系的,体会变中有不变的思想。
学习目标
黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618。这个比例被公认为是最能引起美感的比例,因此被称为黄金分割。
比和比值是什么?我们一起来学习吧!
7
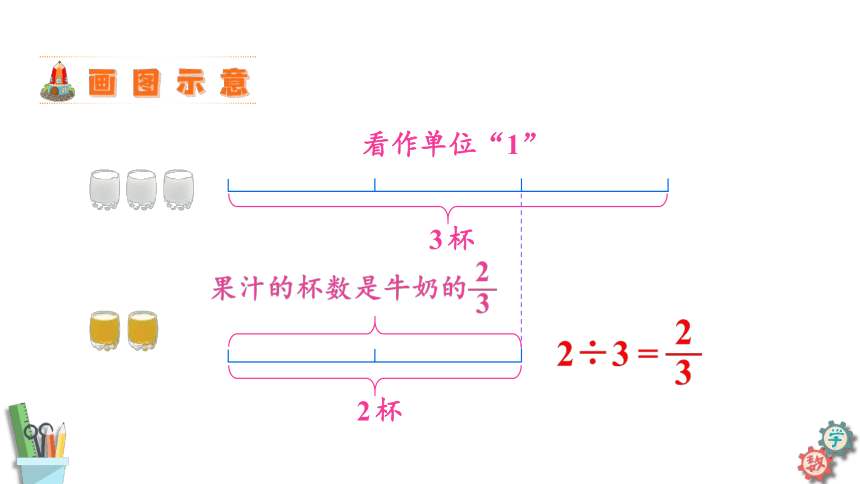
妈妈早晨准备了2杯果汁和3杯牛奶。果汁和牛奶的杯数之间有什么关系?
看作单位“1”
?
2杯
3杯
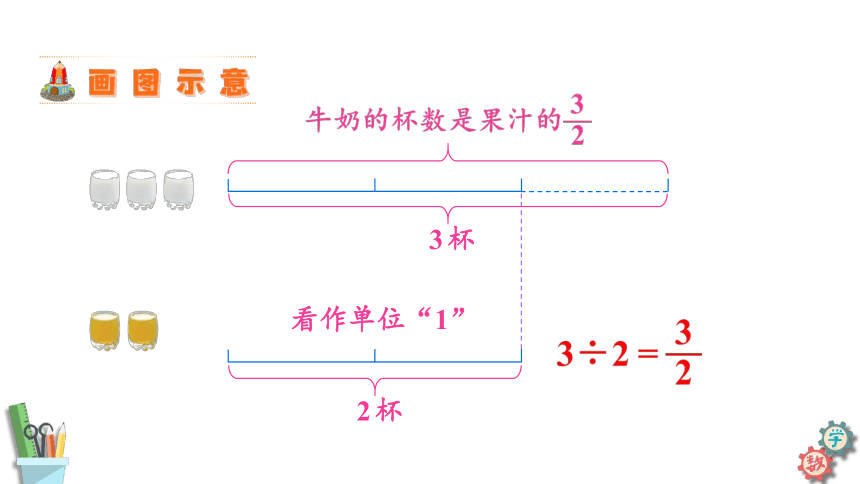
?
看作单位“1”
?
2杯
3杯
?
?
比中各部分的名称如下:
2
:
3
=
2
÷
3
=
?
前项
比
后项
被除数
除号
除数
分子
分母
两个数的比是有顺序的。在用比表示两个数量的关系时,一定要按照前后的顺序,正确表达是哪个数量与哪个数量的比,不能颠倒两个数的位置。
书写时,应先写比号前面的数,再写比号后面的数,顺序不能颠倒。
8
走一段900米长的山路,小军用了15分钟,小伟用了20分钟。你能分别算出他们的速度吗?
速度=路程÷时间
路程
小军所用的时间
小伟所用的时间
8
走一段900米长的山路,小军用了15分钟,小伟用了20分钟。你能分别算出他们的速度吗?
小军的速度:900÷15=60(米/分)
路程
小军所用的时间
小伟所用的时间
小伟的速度:900÷20=45(米/分)
速度=路程÷时间,路程和时间的这种关系也可以用比来表示:
小军走的路程与时间的比是:900:15;
小伟走的路程与时间的比是:900:20;
900:15 =900÷15=60(米/分)
900:20 =900÷20=45(米/分)
900:15 =900÷15=60(米/分)
900:20 =900÷20=45(米/分)
商
两个数相除又可以叫作两个数的比。比的前项除以后项所得的商叫作比值。
前项
后项
比值
从例7、例8中可以看出,两个数相除的关系可以怎样表示?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}比
前项
:(比号)
后项
比值
一种关系
除法
被除数
÷(除号)
除数
商
一种运算
分数
分子
(分数线)
分母
分数值
一个数
?
3:5=( )÷( )=( )
?
3
5
填写上面的等式,想一想:比的前项、后项和比值分别相当于除法算式或分数中的什么?
比的后项可以是0吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}比
前项
:(比号)
后项
比值
一种关系
除法
被除数
÷(除号)
除数
商
一种运算
分数
分子
(分数线)
分母
分数值
一个数
观察上表可以发现,比的前项相当于除法算式中的被除数或分数中的分子,比的后项相当于除法算式中的除数或分数中的分母。因此除数和分母都不能为0,所以比的后项也不能为0。
比、除法、分数之间的区别
4 : 0
各类比赛中的比不是我们这节课学习的比,它只是一种计分形式,是比较大小的,是相差关系,不是相除关系。
数学的比中,比的后项不为0
知识点 1
比的意义
15
12
12
15
15比16
12
15
三
随堂练习
(3)明明买了5支中性笔共用12元,明明买中性笔的总价 与数量的比是( ),比值是( ),这个比值表示的是( )。
单价
12∶5
3 ∶ 5
3 ∶ 8
5 ∶ 2
知识点 2
运用比的意义求一个比的比值的方法
4
=4.9
2.4∶1.8 0.45 t∶200 kg
易错辨析
辨析:没有正确理解比的意义
3.判断。(对的画“√”,错的画“×”)
提升点 1
求比中的未知项
8
15
7.2
四
培优训练
提升点 2
根据分率写比
5
4
3
4
提升点 3
根据等式写比
8∶3
思维拓展
2∶3
比的前项
比的后项
比号
比的意义
比和分数、除法的关系
求比值
a∶b=a÷b= (b≠0)
a
b
五
课堂小结
第6课时 比的认识
1.使学生理解比的意义,会读、写比,认识比的各个部分名称;掌握求比值的方法,能准确地求出比值。 ? ?????
2.使学生理解比、分数、除法之间的联系与区别,通过观察和思考,理解数学知识之间是互相联系的,体会变中有不变的思想。
学习目标
黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618。这个比例被公认为是最能引起美感的比例,因此被称为黄金分割。
比和比值是什么?我们一起来学习吧!
7
妈妈早晨准备了2杯果汁和3杯牛奶。果汁和牛奶的杯数之间有什么关系?
看作单位“1”
?
2杯
3杯
?
看作单位“1”
?
2杯
3杯
?
?
比中各部分的名称如下:
2
:
3
=
2
÷
3
=
?
前项
比
后项
被除数
除号
除数
分子
分母
两个数的比是有顺序的。在用比表示两个数量的关系时,一定要按照前后的顺序,正确表达是哪个数量与哪个数量的比,不能颠倒两个数的位置。
书写时,应先写比号前面的数,再写比号后面的数,顺序不能颠倒。
8
走一段900米长的山路,小军用了15分钟,小伟用了20分钟。你能分别算出他们的速度吗?
速度=路程÷时间
路程
小军所用的时间
小伟所用的时间
8
走一段900米长的山路,小军用了15分钟,小伟用了20分钟。你能分别算出他们的速度吗?
小军的速度:900÷15=60(米/分)
路程
小军所用的时间
小伟所用的时间
小伟的速度:900÷20=45(米/分)
速度=路程÷时间,路程和时间的这种关系也可以用比来表示:
小军走的路程与时间的比是:900:15;
小伟走的路程与时间的比是:900:20;
900:15 =900÷15=60(米/分)
900:20 =900÷20=45(米/分)
900:15 =900÷15=60(米/分)
900:20 =900÷20=45(米/分)
商
两个数相除又可以叫作两个数的比。比的前项除以后项所得的商叫作比值。
前项
后项
比值
从例7、例8中可以看出,两个数相除的关系可以怎样表示?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}比
前项
:(比号)
后项
比值
一种关系
除法
被除数
÷(除号)
除数
商
一种运算
分数
分子
(分数线)
分母
分数值
一个数
?
3:5=( )÷( )=( )
?
3
5
填写上面的等式,想一想:比的前项、后项和比值分别相当于除法算式或分数中的什么?
比的后项可以是0吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}比
前项
:(比号)
后项
比值
一种关系
除法
被除数
÷(除号)
除数
商
一种运算
分数
分子
(分数线)
分母
分数值
一个数
观察上表可以发现,比的前项相当于除法算式中的被除数或分数中的分子,比的后项相当于除法算式中的除数或分数中的分母。因此除数和分母都不能为0,所以比的后项也不能为0。
比、除法、分数之间的区别
4 : 0
各类比赛中的比不是我们这节课学习的比,它只是一种计分形式,是比较大小的,是相差关系,不是相除关系。
数学的比中,比的后项不为0
知识点 1
比的意义
15
12
12
15
15比16
12
15
三
随堂练习
(3)明明买了5支中性笔共用12元,明明买中性笔的总价 与数量的比是( ),比值是( ),这个比值表示的是( )。
单价
12∶5
3 ∶ 5
3 ∶ 8
5 ∶ 2
知识点 2
运用比的意义求一个比的比值的方法
4
=4.9
2.4∶1.8 0.45 t∶200 kg
易错辨析
辨析:没有正确理解比的意义
3.判断。(对的画“√”,错的画“×”)
提升点 1
求比中的未知项
8
15
7.2
四
培优训练
提升点 2
根据分率写比
5
4
3
4
提升点 3
根据等式写比
8∶3
思维拓展
2∶3
比的前项
比的后项
比号
比的意义
比和分数、除法的关系
求比值
a∶b=a÷b= (b≠0)
a
b
五
课堂小结
