(人教新课标)六年级数学下册教案 圆柱的认识与表面积
文档属性
| 名称 | (人教新课标)六年级数学下册教案 圆柱的认识与表面积 |

|
|
| 格式 | zip | ||
| 文件大小 | 51.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-17 00:00:00 | ||
图片预览

文档简介
圆柱的认识与表面积
【教学目的】
1.使学生认识圆柱的特征,能看懂圆柱的平面图;认识圆柱侧面的展开图。
2.理解圆柱侧面积和圆柱表面积的含义,掌握圆柱侧面积和表面积的计算方法。
3.根据圆柱的表面积与侧面积的关系使学生学会运用所学的知识解决简单的实际问题。
【教学过程】
一、复习:
师:出示各种平面图形,让学生指出各图形面积的计算方法。重点突出圆的面积求解方法,并引出圆周长的求解方法。
使学生熟悉圆的周长和面积公式:S =πr2,C=2πr或C=πd。
二、新课
1.导入新课
教师手中先后拿一个长方体形的物体和正方体形的物体,提问:我手里拿的物体是什么形状的?他们有什么特征?引导学生复习长方体和正方体的一些特征。
教师出示例题图例:观察下面这些物体,它们有什么特点?
2.圆柱的认识。
让学生拿着圆柱形的物体观察后,说出自己观察的结果。认识圆柱体的外部特征以及与长方体与正方体的区别。
总结:长方体、正方体都是由平面围成的立体图形;而圆柱则有一个曲面,有两个面是圆,从上到下一样粗细,等等。
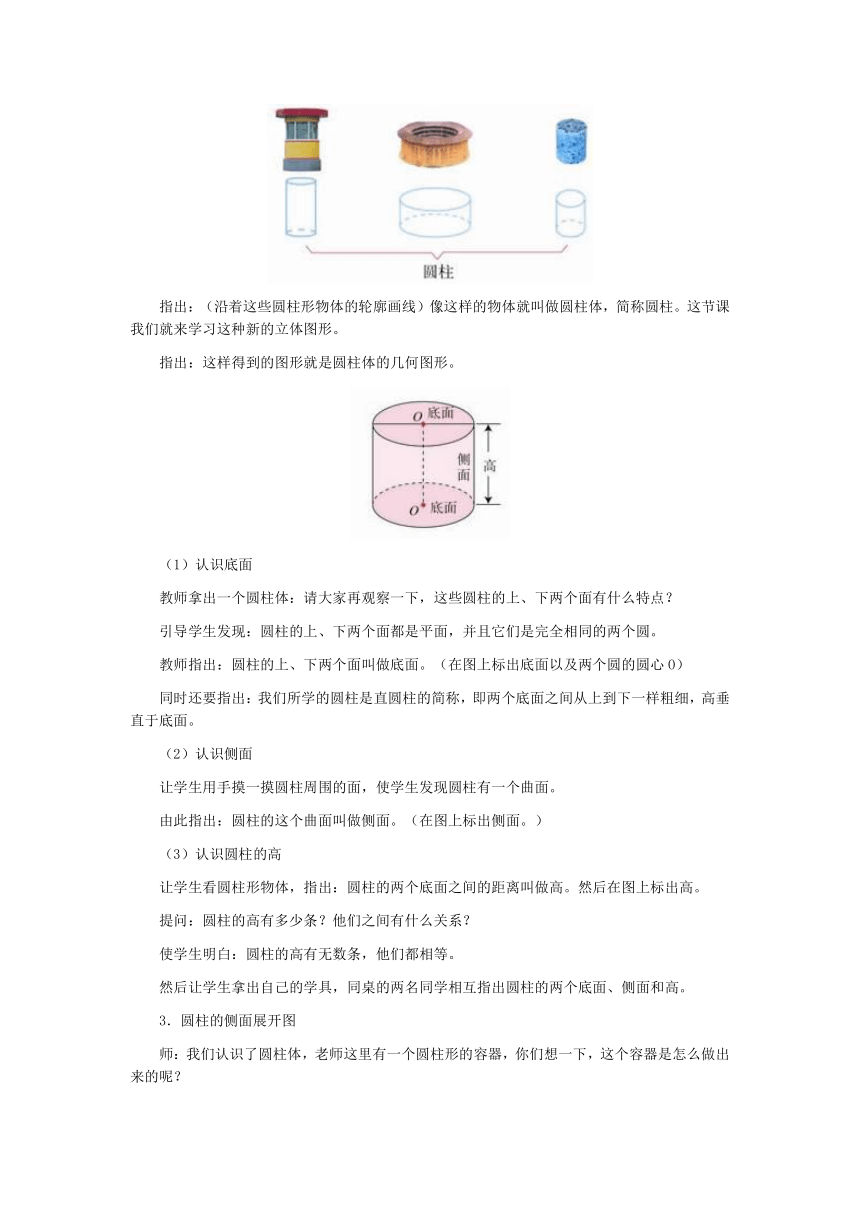
指出:(沿着这些圆柱形物体的轮廓画线)像这样的物体就叫做圆柱体,简称圆柱。这节课我们就来学习这种新的立体图形。
指出:这样得到的图形就是圆柱体的几何图形。
(1)认识底面
教师拿出一个圆柱体:请大家再观察一下,这些圆柱的上、下两个面有什么特点?
引导学生发现:圆柱的上、下两个面都是平面,并且它们是完全相同的两个圆。
教师指出:圆柱的上、下两个面叫做底面。(在图上标出底面以及两个圆的圆心O)
同时还要指出:我们所学的圆柱是直圆柱的简称,即两个底面之间从上到下一样粗细,高垂直于底面。
(2)认识侧面
让学生用手摸一摸圆柱周围的面,使学生发现圆柱有一个曲面。
由此指出:圆柱的这个曲面叫做侧面。(在图上标出侧面。)
(3)认识圆柱的高
让学生看圆柱形物体,指出:圆柱的两个底面之间的距离叫做高。然后在图上标出高。
提问:圆柱的高有多少条?他们之间有什么关系?
使学生明白:圆柱的高有无数条,他们都相等。
然后让学生拿出自己的学具,同桌的两名同学相互指出圆柱的两个底面、侧面和高。
3.圆柱的侧面展开图
师:我们认识了圆柱体,老师这里有一个圆柱形的容器,你们想一下,这个容器是怎么做出来的呢?
指导学生分析自己手中的模型,得出圆柱的侧面展开图。
教师出示罐头盒,沿着罐头盒的一条高剪开商标纸,再打开,展开在黑板上,得到的是一个长方形。
教师:这个展开后的长方形它的长宽与圆柱体有什么关系呢?
学生:这个长方形的长等于圆柱的周长,长方形的宽等于圆往的高。
教师:那么,圆柱侧面积应该怎样计算呢?下面我们就来算一下圆柱的侧面积和表面积。
4.圆柱的侧面积。
教师:圆柱的侧面积,顾名思义,也就是圆柱侧面的面积。(教师边叙述边摸着圆柱的侧面演示给学生看,指出侧面的大小就是圆柱的侧面积)。
教师:从上面的实验我们可以看出,这个展开后的长方形的面积和圆柱的侧面积有什么关系呢?(教师出示圆柱的侧面展开图,让学生观察很容易看到这个长方形的面积等于圆柱的例面积。)
教师:那么,圆柱的侧面积应该怎样计算呢
引导学生根据展开后的长方形的长和宽与圆柱底面周长和高的关系,可以知道:
圆柱的侧面积=底面周长×高
教师:圆柱底面的周长就是底面圆的周长,如果我们知道底面的半径r和圆柱的高h
则:
圆柱的侧面积:S=2πr h
小结:
要计算圆柱的侧面积,必须知道圆柱底面周长和高这两个条件,有时题里只给出直径或半径,底面周长这个条件可以通过计算得到,在解题前要注意看清题意再列式。
5.圆柱的表面积
教师:请大家把上节课自己制作的圆柱模型展开,观察一下,圆柱的表面由哪几个部分组成
通过操作,使学生认识到:圆柱的表面由上、下两个底面和侧面组成。
教师指着圆柱的展开图,“那么,圆柱的表面积是什么?”
指名学生回答,使大家明确:圆柱的表面积是指圆柱表面的面积,也就是圆柱的侧面积加上两个底面的面积。
圆柱的表面积=圆柱侧面积十两个底面的面积
三、应用
教师:我们看过圆柱的展开图后,知道了圆柱的侧面展开是一个矩形,这样圆柱的侧面积就是圆柱的底面周长与高的乘积,进而侧面积加上两个底面的面积就是圆柱的表面积,下面我们就来实际应用一下:
教师出示例题4:一顶厨师帽,高 28cm,帽顶直径 20cm,做这样一顶帽子至少需要用多少面料?(得数保留整十平方厘米。)
教师:这道题目已知什么,要求什么?你觉得该怎样求?(学生分组讨论:是求圆柱形的表面积,但是需要少算一个底面的面积)
教师:要计算做这个帽子需要用多少面料,我们可以用求解圆柱体面积的方法得到,那么,应该分哪几步
指名学生回答后,指定两名学生板演,其他学生独立进行计算。教师行间巡视,注意察看最后的得数是否计算正确。
做完后,集体订正。指名学生回答自己在计算时,最后的得数是怎样取舍的。由此指出:这道题使用的材料要比计算得到的结果多一些。因此,这里不能用四舍五人法取近似值。这道题要保留整百平方厘米,省略的十位上即使是4或比4小,都要向前一位进1。这种取近似值的方法叫做进一法。
小结:在实际应用中计算圆柱形物体的表面积,要根据实际情况计算各部分的面积。如计算烟筒用铁皮只求一个侧面积,水桶用铁皮是侧面积加上一个底面积,油桶用铁皮是侧面积加上两个底面积,求用料多少,一般采用进一法取值,以保证原材料够用。
四、巩固练习
完成课后题目。
【教学目的】
1.使学生认识圆柱的特征,能看懂圆柱的平面图;认识圆柱侧面的展开图。
2.理解圆柱侧面积和圆柱表面积的含义,掌握圆柱侧面积和表面积的计算方法。
3.根据圆柱的表面积与侧面积的关系使学生学会运用所学的知识解决简单的实际问题。
【教学过程】
一、复习:
师:出示各种平面图形,让学生指出各图形面积的计算方法。重点突出圆的面积求解方法,并引出圆周长的求解方法。
使学生熟悉圆的周长和面积公式:S =πr2,C=2πr或C=πd。
二、新课
1.导入新课
教师手中先后拿一个长方体形的物体和正方体形的物体,提问:我手里拿的物体是什么形状的?他们有什么特征?引导学生复习长方体和正方体的一些特征。
教师出示例题图例:观察下面这些物体,它们有什么特点?
2.圆柱的认识。
让学生拿着圆柱形的物体观察后,说出自己观察的结果。认识圆柱体的外部特征以及与长方体与正方体的区别。
总结:长方体、正方体都是由平面围成的立体图形;而圆柱则有一个曲面,有两个面是圆,从上到下一样粗细,等等。
指出:(沿着这些圆柱形物体的轮廓画线)像这样的物体就叫做圆柱体,简称圆柱。这节课我们就来学习这种新的立体图形。
指出:这样得到的图形就是圆柱体的几何图形。
(1)认识底面
教师拿出一个圆柱体:请大家再观察一下,这些圆柱的上、下两个面有什么特点?
引导学生发现:圆柱的上、下两个面都是平面,并且它们是完全相同的两个圆。
教师指出:圆柱的上、下两个面叫做底面。(在图上标出底面以及两个圆的圆心O)
同时还要指出:我们所学的圆柱是直圆柱的简称,即两个底面之间从上到下一样粗细,高垂直于底面。
(2)认识侧面
让学生用手摸一摸圆柱周围的面,使学生发现圆柱有一个曲面。
由此指出:圆柱的这个曲面叫做侧面。(在图上标出侧面。)
(3)认识圆柱的高
让学生看圆柱形物体,指出:圆柱的两个底面之间的距离叫做高。然后在图上标出高。
提问:圆柱的高有多少条?他们之间有什么关系?
使学生明白:圆柱的高有无数条,他们都相等。
然后让学生拿出自己的学具,同桌的两名同学相互指出圆柱的两个底面、侧面和高。
3.圆柱的侧面展开图
师:我们认识了圆柱体,老师这里有一个圆柱形的容器,你们想一下,这个容器是怎么做出来的呢?
指导学生分析自己手中的模型,得出圆柱的侧面展开图。
教师出示罐头盒,沿着罐头盒的一条高剪开商标纸,再打开,展开在黑板上,得到的是一个长方形。
教师:这个展开后的长方形它的长宽与圆柱体有什么关系呢?
学生:这个长方形的长等于圆柱的周长,长方形的宽等于圆往的高。
教师:那么,圆柱侧面积应该怎样计算呢?下面我们就来算一下圆柱的侧面积和表面积。
4.圆柱的侧面积。
教师:圆柱的侧面积,顾名思义,也就是圆柱侧面的面积。(教师边叙述边摸着圆柱的侧面演示给学生看,指出侧面的大小就是圆柱的侧面积)。
教师:从上面的实验我们可以看出,这个展开后的长方形的面积和圆柱的侧面积有什么关系呢?(教师出示圆柱的侧面展开图,让学生观察很容易看到这个长方形的面积等于圆柱的例面积。)
教师:那么,圆柱的侧面积应该怎样计算呢
引导学生根据展开后的长方形的长和宽与圆柱底面周长和高的关系,可以知道:
圆柱的侧面积=底面周长×高
教师:圆柱底面的周长就是底面圆的周长,如果我们知道底面的半径r和圆柱的高h
则:
圆柱的侧面积:S=2πr h
小结:
要计算圆柱的侧面积,必须知道圆柱底面周长和高这两个条件,有时题里只给出直径或半径,底面周长这个条件可以通过计算得到,在解题前要注意看清题意再列式。
5.圆柱的表面积
教师:请大家把上节课自己制作的圆柱模型展开,观察一下,圆柱的表面由哪几个部分组成
通过操作,使学生认识到:圆柱的表面由上、下两个底面和侧面组成。
教师指着圆柱的展开图,“那么,圆柱的表面积是什么?”
指名学生回答,使大家明确:圆柱的表面积是指圆柱表面的面积,也就是圆柱的侧面积加上两个底面的面积。
圆柱的表面积=圆柱侧面积十两个底面的面积
三、应用
教师:我们看过圆柱的展开图后,知道了圆柱的侧面展开是一个矩形,这样圆柱的侧面积就是圆柱的底面周长与高的乘积,进而侧面积加上两个底面的面积就是圆柱的表面积,下面我们就来实际应用一下:
教师出示例题4:一顶厨师帽,高 28cm,帽顶直径 20cm,做这样一顶帽子至少需要用多少面料?(得数保留整十平方厘米。)
教师:这道题目已知什么,要求什么?你觉得该怎样求?(学生分组讨论:是求圆柱形的表面积,但是需要少算一个底面的面积)
教师:要计算做这个帽子需要用多少面料,我们可以用求解圆柱体面积的方法得到,那么,应该分哪几步
指名学生回答后,指定两名学生板演,其他学生独立进行计算。教师行间巡视,注意察看最后的得数是否计算正确。
做完后,集体订正。指名学生回答自己在计算时,最后的得数是怎样取舍的。由此指出:这道题使用的材料要比计算得到的结果多一些。因此,这里不能用四舍五人法取近似值。这道题要保留整百平方厘米,省略的十位上即使是4或比4小,都要向前一位进1。这种取近似值的方法叫做进一法。
小结:在实际应用中计算圆柱形物体的表面积,要根据实际情况计算各部分的面积。如计算烟筒用铁皮只求一个侧面积,水桶用铁皮是侧面积加上一个底面积,油桶用铁皮是侧面积加上两个底面积,求用料多少,一般采用进一法取值,以保证原材料够用。
四、巩固练习
完成课后题目。
