安徽省芜湖市2020-2021学年高一下学期期末考试数学试题 PDF版含答案
文档属性
| 名称 | 安徽省芜湖市2020-2021学年高一下学期期末考试数学试题 PDF版含答案 |

|
|
| 格式 | |||
| 文件大小 | 483.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 00:00:00 | ||
图片预览



文档简介
20— 202 1 学 年 度 第 二 学 期 芜 湖 市 中 小 学 校 教 育 教 学 质 量 监 控
高一年级数学试题卷
一 、 单选题 ( 本大题共 12 小题 , 每小题 3 分 , 共 36 分 , 在每小题给出的四个选项中 , 只有一项是符合
题目要求的 )
1? 数 列 - 1 , 3 , - 5 , 7 … 的 一 个 通 项 公 式 为
n+ 1
A ? a n = 2 n- 1 B ? a n = ( - 1 ) × ( 2 n- 1 )
n n
C ? a n = ( - 1 ) × ( 2 n- 1 ) D ? a n = ( - 1 ) × ( 2 n+ 1 )
2? 现 要 完 成 下 列 3 项 抽 样 调 查 : ① 从 10 盒 酸 奶 中 抽 取 3 盒 进 行 食 品 卫 生 检 查 ; ② 科 技 报 告 厅
有 32 排 , 每排有 40 个座位 , 有一次报告会恰好坐满了听众 , 报告会结束后 , 为了听取意见 ,
需要请 32 名听众进行座谈 ; ③ 某中学共有 160 名教职工 , 其中一般教师 120 名 , 行政人员 16
名 , 后勤人员 24 名 , 为了了解教职工对学校在校务公开方面的意见 , 拟抽取一个容量为 20
的样本 ? 其中较为合理的抽样方法是
A ? 简 单 随 机 抽 样 , 系 统 抽 样 , 分 层 抽 样 B ? 简 单 随 机 抽 样 , 分 层 抽 样 , 系 统 抽 样
C ? 系 统 抽 样 , 简 单 随 机 抽 样 , 分 层 抽 样 D ? 分 层 抽 样 , 系 统 抽 样 , 简 单 随 机 抽 样
3? 下 列 命 题 中 , 正 确 的 是
2 2 1 1
A ? 若 a<b , 则 ac <bc B ? 若 a>b> 0 , 则
C ? a > b 则 a > b D a > b > , c < d < , 则 a c > b d
x - y 0
x , y 2 y ≤ 0 x - y
1 ≤
A B C D
x 、 y 一 组 数 据 如 表 所 示 y 与 x 的 回 归 直 线 方 程 为 3 x + a 则 a
x
y -
A - 1 B ? 1 . 5
C ? 2 D ? 1
6
A ? 3
B ? 7
C ? 1 5
D ? 1 2
芜 湖 市 高 一 数 学 试 题 卷 第 页 ( 共 6
7 ? 我 国 古 代 数 学 典 籍 《 九 章 算 术 》 第 七 章 “ 盈 不 足 ” 中 有 一 道 两 鼠 穿 墙 问 题 : “ 今 有 垣 厚 五 尺 ,
两 鼠 对 穿 , 大 鼠 日 一 尺 , 小 鼠 日 一 尺 , 大 鼠 日 自 倍 , 小 鼠 日 自 半 , 问 何 日 相 逢 ” , 翻 译 过 来 就
是 : 有 五 尺 厚 的 墙 , 两 只 老 鼠 从 墙 的 两 边 相 对 分 别 打 洞 穿 墙 , 大 、 小 鼠 第 一 天 都 进 一 尺 , 以 后
每 天 , 大 鼠 加 倍 , 小 鼠 减 半 , 则 在 第 几 天 两 鼠 相 遇 . 这 个 问 题 体 现 了 古 代 对 数 列 问 题 的 研 究 ,
现 将 墙 的 厚 度 改 为 1 3 0 尺 , 则 在 第 几 天 墙 才 能 被 打 穿 ?
A ? 6 B ? 7 C ? 8 D ? 9
8 ? 设 △ A B C 的 内 角 A , B , C 所 对 的 边 分 别 为 a , b , c , 若 2 a c o s B = c , 则 △ A B C 的 形 状 一 定 是
A ? 直 角 三 角 形 B ? 等 腰 直 角 三 角 形 C ? 等 腰 三 角 形 D ? 等 边 三 角 形
S 4 1 S 8
9 ? 设 S n 是 等 差 数 列 { a n } 的 前 n 项 和 , 若 = , 则 =
S 8 3 S 16
3 3 1 1
A ? B ? C ? D ?
5 1 0 2 5
2
1 0 ? 当 x ∈ R 时 , 不 等 式 k x - k x + 2 > 0 恒 成 立 , 则 k 的 取 值 范 围 是
A ? ( - ∞ , 0 ] ∪ ( 8 , + ∞ ) B ? [ 0 , + ∞ )
C ? ( 0 , 8 ) D ? [ 0 , 8 )
1 1 ? 如 图 , 某 景 区 欲 在 两 山 顶 A , C 之 间 建 缆 车 , 需 要 测 量 两 山 顶 间 的 距
离 . 已 知 山 高 A B =
槡 3 ( k m ) , C D = 3
槡 3 ( k m ) , 在 水 平 面 上 E 处 测 得 山
顶 A 的 仰 角 为 3 0 ° , 山 顶 C 的 仰 角 为 4 5 ° , ∠ B E D = 1 5 0 ° , 则 两 山 顶 A 、
C 之 间 的 距 离 为
A ?
槡 6 3 ( k m ) B ? 5
槡 3 ( k m )
C ?
槡 1 3 ( k m ) D ?
槡 6 6 ( k m )
2 2
1 2 ? 已 知 方 程 x + b x + c = 0 , 在 ( 0 , 2 ) 上 有 两 个 不 同 的 解 , 则 c + 2 ( b + 2 ) c 的 取 值 范 围 是
2 3
A ? ( 0 , 槡 ) B ? ( 0 , ) C ? ( 0 , 1 ) D ? ( 0 , 2 )
2 4 槡
二 、 填 空 题 ( 本 大 题 共 4 小 题 , 每 小 题 4 分 , 共 1 6 分 )
1 3 . 抛 掷 甲 、 乙 两 枚 质 地 均 匀 且 各 面 分 别 标 有 1 , 2 , 3 , 4 , 5 , 6 的 骰 子 , 记 正 面 向 上 的 数 字 分 别 为
x , y , 则 x < y 的 概 率 是 ?
4
1 4 ? 函 数 y = x + + 2 ( x > 0 ) 的 最 小 值 为 .
x + 1
4
1 5 ? 已 知 数 列 { a n } 满 足 a n + 1 = 且 a 1 = 4 , S n 为 数 列 { a n } 的 前 项 和 , 则 S 2020 = .
2 - a n
1 6 ? 在 △ A B C 中 , 已 知 槡 2 a = 4 c o s C +
槡 2 c s i n B , b = 2
槡 2 , 则 △ A B C 面 积 的 最 大 值 是 ?
芜 湖 市 高 一 数 学 试 题 卷 第 2 页 ( 共 6 页 )
三 、 解 答 题 ( 本 大 题 共 5 小 题 , 共 4 8 分 ? 解 答 应 写 出 文 字 说 明 , 证 明 过 程 或 演 算 步 骤 )
1 7 ? ( 本 小 题 满 分 8 分 )
2
已 知 函 数 f ( x ) = x - ( 3 a + 1 ) x + b ?
( 1 ) 当 a = 1 , b = - 5 时 , 解 不 等 式 f ( x ) > 0 ;
2
( 2 ) 当 b = 2 a + 2 a 时 , 解 关 于 x 的 不 等 式 f ( x ) < 0 ( 结 果 用 a 表 示 ) ?
1 8 ? ( 本 小 题 满 分 1 0 分 )
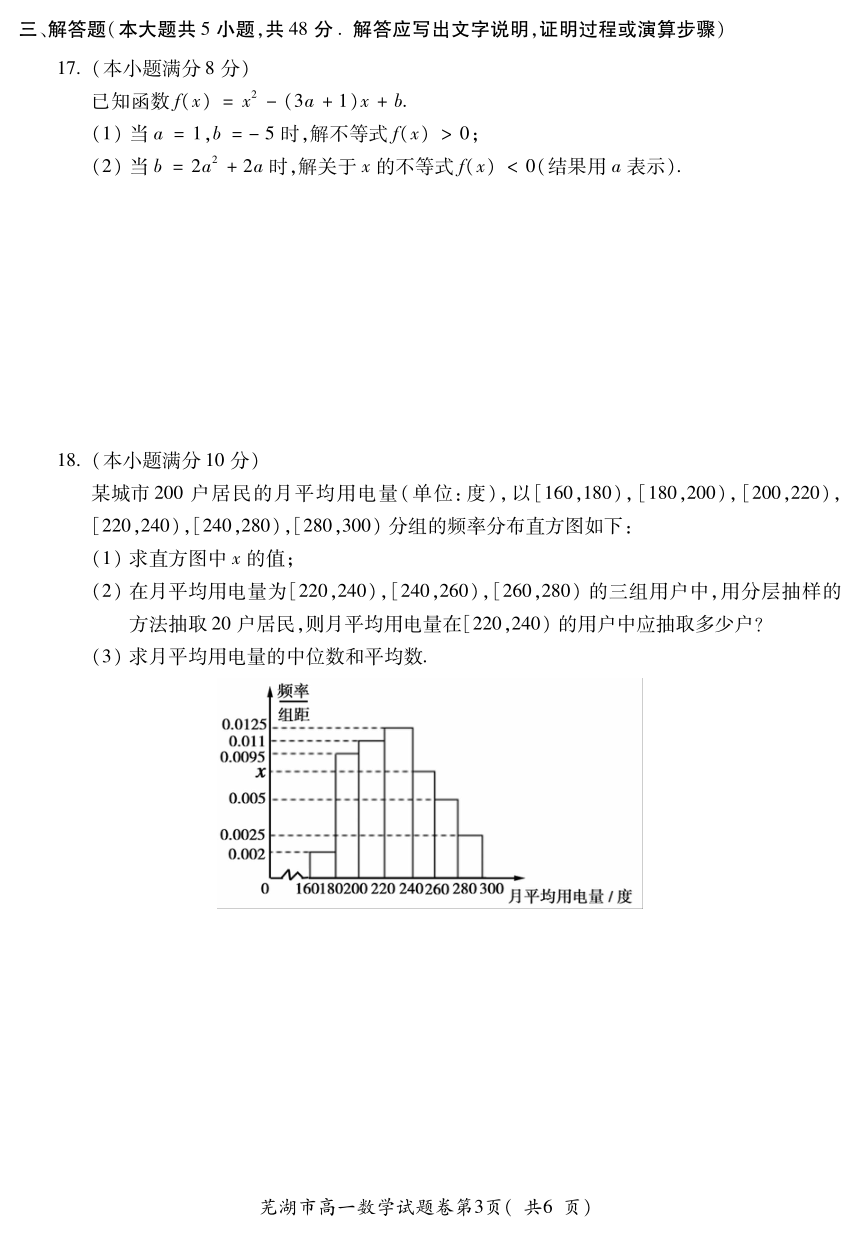
某 城 市 2 0 0 户 居 民 的 月 平 均 用 电 量 ( 单 位 : 度 ) , 以 [ 1 6 0 , 1 8 0 ) , [ 1 8 0 , 2 0 0 ) , [ 2 0 0 , 2 2 0 ) ,
[ 2 2 0 , 2 4 0 ) , [ 2 4 0 , 2 8 0 ) , [ 2 8 0 , 3 0 0 ) 分 组 的 频 率 分 布 直 方 图 如 下 :
( 1 ) 求 直 方 图 中 x 的 值 ;
( 2 ) 在 月 平 均 用 电 量 为 [ 2 2 0 , 2 4 0 ) , [ 2 4 0 , 2 6 0 ) , [ 2 6 0 , 2 8 0 ) 的 三 组 用 户 中 , 用 分 层 抽 样 的
方 法 抽 取 2 0 户 居 民 , 则 月 平 均 用 电 量 在 [ 2 2 0 , 2 4 0 ) 的 用 户 中 应 抽 取 多 少 户 ?
( 3 ) 求 月 平 均 用 电 量 的 中 位 数 和 平 均 数 .
芜 湖 市 高 一 数 学 试 题 卷 第 3 页 ( 共 6 页 )
1 9 ? ( 本 小 题 满 分 1 0 分 ) s i n A - s i n C a - b
在 △ A B C 中 , 内 角 A , B , C 的 对 边 分 别 是 a , b , c , 且 = .
s i n B a + c
( 1 ) 求 角 C 的 大 小 ;
( 2 ) 若 c = 4
槡 3 , 且 A B 边 上 的 中 线 长 为 5 , 求 △ A B C 的 面 积 .
芜 湖 市 高 一 数 学 试 题 卷 第 4 页 ( 共 6 页 )
2 0 . ( 本 小 题 满 分 1 0 分 )
n + 1
2 a n ?
已 知 数 列 { a n } 满 足 a 1 = 1 , a n + 1 = n ( n ∈ N ) ?
a n + 2
n
( 1 ) 2
证 明 : 数 列 { 是 等 差 数 列 , 并 求 数 列 { a n } 的 通 项 公 式 ;
a n }
( 2 ) 设 b n = n ( n + 1 ) a n , 求 数 列 { b n } 的 前 n 项 和 S n .
芜 湖 市 高 一 数 学 试 题 卷 第 5 页 ( 共 6 页 )
2 1 . ( 本 小 题 满 分 1 0 分 )
如 图 , 芜 湖 市 城 乡 规 划 局 将 龙 窝 湖 定 位 为 市 级 滨 江 湿 地 公 园 , 现 准 备 在 湿 地 内 建 造 一 个 观
景 台 P , 已 知 射 线 A B , A C 为 湿 地 两 边 夹 角 为 1 2 0 ° 的 公 路 且 长 度 均 超 过 2 千 米 , 在 两 条 公 路
A B , A C 上 分 别 设 立 游 客 接 送 点 M , N , 从 观 景 台 P 到 M , N 建 造 两 条 观 光 线 路 P M , P N , 测 得
A M = 2 千 米 , A N = 2 千 米 ?
( 1 ) 求 线 段 M N 的 长 度 ;
( 2 ) 若 ∠ M P N = 6 0 ° , 求 两 条 观 光 线 路 P M 与 P N 之 和 的 最 大 值 ?
芜 湖 市 高 一 数 学 试 题 卷 第 6 页 ( 共 6 页 )
20— 202 1 学 年 度 第 二 学 期 芜 湖 市 中 小 学 校 教 育 教 学 质 量 监 控
高一年级数学参考答案及评分标准 ( 必 修 数 学 ③⑤ )
一 、 选择题 ( 本大题共 12 小题 , 每小题 3 分 , 共 36 分 )
题 号 1 2 3 4 5 6 7 8 9 10 11 12
答 案 C A B D B C C C B D B C
二 、 填空题 ( 本大题共 4 个小题 , 每小题 4 分 , 共 16 分 )
5
13 ? 1 4 ? 5 1 5 ? 2 0 2 3 1 6 ? 2 2 + 1 )
1 2
、 ( , )
( 本 小 题 满 分 分 )
( ) , b = - f ( x ) = x - 4 x - = ( x + ) ( )
f ( x ) > 0 - - 1 ) ( 5 , + 3
2 ) a + 2 a f ( x ) = x - ( 3 a + ) x + a + 2 a = x - a ) [ ( a + ) ]
( x ) < 0 x - a ) [ ( a + ) ] 0 5
当 时 2 a > a + , ( a + , 2 a ) 6
当 时 2 a = a + , 7
当 时 2 a < a + , ( 2 a , a + ) 8
1 8 ? 本 小 题 满 分 分 )
( ) 由 直 方 图 的 性 质 可 得
0 . 0 0 2 0 . 0 0 9 5 0 . 0 1 1 0 . 0 1 2 5 0 . 0 0 5 0 . 0 0 2 5 × 2 0 1
: x = . 0 0 7 5 所 以 直 方 图 中 的 值 是 . 0 0 7 5 … … … … … … … … … … … … … 2 分
2 ) 月 平 均 用 电 量 比 例 为 5
所 以 月 平 均 用 电 量 在 2 2 0 2 4 0 2 0 1 0 ? 5
1 0
3 ) ( 0 . 0 0 2 0 . 0 0 9 5 0 . 0 1 1 × 2 0 0 . 4 5 0 . 5 ,
卷 [ 2 2 0 2 4 0 内 , 设 中 位 数 为 ,
( 0 . 0 0 2 0 . 0 0 9 5 0 . 0 1 1 × 2 0 0 . 0 1 2 5 ( a - = 0 . 5
a = . 7
1 7 0 0 . 0 4 1 9 0 0 . 1 9 2 1 0 0 . 2 2 2 3 0 0 . 2 5 2 5 0 0 . 1 5 2 7 0
0 . 1 + 2 9 0 0 . 0 5 9
2 2 5 6 1 0
1 9 ? 1 0
1 ) 由 正 弦 定 理 得 化 简 得 … … … … … … … … … … 分
由 余 弦 定 理 得
芜 湖 市 高 一 数 学 试 题 卷 答 案 第 页 ( 共
π
由 C ∈ ( 0 , π ) 可 得 C = ; … … … … … … … … … … … … … … … … … … … … … 4 分
3
( 2 ) 倍 长 A B 边 上 的 中 线 至 C D , 连 接 D A , 在 △ D A C 中 由 ∠ C A D 的 余 弦 定 理 可 得
2 2
a + b - 1 0 0 1 2 2
c o s ∠ C A D = = - ? a + b + a b = 1 0 0 … … … … … … … … … 8 分
2 a b 2
2 2 2 2 2
又 由 ( 1 ) 知 a + b - c = a b 即 a + b - 4 8 = a b
所 以 a b = 2 6 ,
1 1 3 1 3 3
所 以 S = a b s i n C = × 2 6 × 槡 = 槡 … … … … … … … … … … … … … … 1 0 分
2 2 2 2
2 0 . ( 本 小 题 满 分 1 0 分 )
a n + 1 n n + 1 n
n + 1 a n 2 2 2 2
( 1 ) 由 已 知 可 得 n + 1 = n , 所 以 = + 1 , 即 - = 1 ,
2 a n + 2 a n + 1 a n a n + 1 a n
n
∴ 2
数 列 { 是 公 差 为 1 的 等 差 数 列 , … … … … … … … … … … … … … … … … … … 3 分
a n }
n
2 2
∴ = + ( n - 1 ) · 1 = n + 1 ,
a n a 1
n
2
∴ a n = . … … … … … … … … … … … … … … … … … … … … … … … … … … … … 4 分
n + 1
n
( 2 ) 由 ( 1 ) 知 , b n = n · 2 , … … … … … … … … … … … … … … … … … … … … … … … … 5 分
2 3 n
所 以 S n = 1 · 2 + 2 · 2 + 3 · 2 + … + n · 2 ,
2 3 4 n + 1
2 S n = 1 · 2 + 2 · 2 + 3 · 2 + … + n · 2 ,
2 3 n n + 1 n + 1 n + 1
相 减 得 - S n = 2 + 2 + 2 + … + 2 - n · 2 = 2 - 2 - n · 2 ,
n + 1
∴ S n = ( n - 1 ) 2 + 2 ? … … … … … … … … … … … … … … … … … … … … … … 1 0 分
2 1 . ( 本 小 题 满 分 1 0 分 )
( 1 ) 在 △ A M N 中 , 由 余 弦 定 理 得 ,
2 2 2 2 2 1
M N = A M + A N - 2 A M · A N c o s 1 2 0 ° = 2 + 2 - 2 × 2 × 2 × ( - ) = 1 2 ,
2
所 以 M N = 2
槡 3 千 米 ? … … … … … … … … … … … … … … … … … … … … … … … … 3 分
( 2 ) 设 ∠ P M N = α , 因 为 ∠ M P N = 6 0 ° , 所 以 ∠ P N M = 1 2 0 ° - α ,
M N P M P N
在 △ P M N 中 , 由 正 弦 定 理 得 , = = = 4
s i n ∠ M P N s i n ( 1 2 0 ° - α ) s i n α
所 以 P M = 4 s i n ( 1 2 0 ° - α ) , P N = 4 s i n α … … … … … … … … … … … … … … … … 5 分
3 1
所 以 P M + P N = 4 s i n ( 1 2 0 ° - α ) + 4 s i n α = 4 ( 槡 c o s α + s i n α ) + 4 s i n α
2 2
= 6 s i n α + 2
槡 3 c o s α = 4
槡 3 s i n ( α + 3 0 ° ) , … … … … … … … … … … … … … … … … 8 分
因 为 0 ° < α < 1 2 0 ° , 所 以 3 0 ° < α + 3 0 ° < 1 5 0 ° ,
所 以 当 α + 3 0 ° = 9 0 ° , 即 α = 6 0 ° 时 , P M + P N 取 到 最 大 值 4
槡 3 ?
答 : 两 条 观 光 线 路 距 离 之 和 的 最 大 值 为 4
槡 3 千 米 ? … … … … … … … … … … … 1 0 分
芜 湖 市 高 一 数 学 试 题 卷 答 案 第 2 页 ( 共 2 页 )
高一年级数学试题卷
一 、 单选题 ( 本大题共 12 小题 , 每小题 3 分 , 共 36 分 , 在每小题给出的四个选项中 , 只有一项是符合
题目要求的 )
1? 数 列 - 1 , 3 , - 5 , 7 … 的 一 个 通 项 公 式 为
n+ 1
A ? a n = 2 n- 1 B ? a n = ( - 1 ) × ( 2 n- 1 )
n n
C ? a n = ( - 1 ) × ( 2 n- 1 ) D ? a n = ( - 1 ) × ( 2 n+ 1 )
2? 现 要 完 成 下 列 3 项 抽 样 调 查 : ① 从 10 盒 酸 奶 中 抽 取 3 盒 进 行 食 品 卫 生 检 查 ; ② 科 技 报 告 厅
有 32 排 , 每排有 40 个座位 , 有一次报告会恰好坐满了听众 , 报告会结束后 , 为了听取意见 ,
需要请 32 名听众进行座谈 ; ③ 某中学共有 160 名教职工 , 其中一般教师 120 名 , 行政人员 16
名 , 后勤人员 24 名 , 为了了解教职工对学校在校务公开方面的意见 , 拟抽取一个容量为 20
的样本 ? 其中较为合理的抽样方法是
A ? 简 单 随 机 抽 样 , 系 统 抽 样 , 分 层 抽 样 B ? 简 单 随 机 抽 样 , 分 层 抽 样 , 系 统 抽 样
C ? 系 统 抽 样 , 简 单 随 机 抽 样 , 分 层 抽 样 D ? 分 层 抽 样 , 系 统 抽 样 , 简 单 随 机 抽 样
3? 下 列 命 题 中 , 正 确 的 是
2 2 1 1
A ? 若 a<b , 则 ac <bc B ? 若 a>b> 0 , 则
C ? a > b 则 a > b D a > b > , c < d < , 则 a c > b d
x - y 0
x , y 2 y ≤ 0 x - y
1 ≤
A B C D
x 、 y 一 组 数 据 如 表 所 示 y 与 x 的 回 归 直 线 方 程 为 3 x + a 则 a
x
y -
A - 1 B ? 1 . 5
C ? 2 D ? 1
6
A ? 3
B ? 7
C ? 1 5
D ? 1 2
芜 湖 市 高 一 数 学 试 题 卷 第 页 ( 共 6
7 ? 我 国 古 代 数 学 典 籍 《 九 章 算 术 》 第 七 章 “ 盈 不 足 ” 中 有 一 道 两 鼠 穿 墙 问 题 : “ 今 有 垣 厚 五 尺 ,
两 鼠 对 穿 , 大 鼠 日 一 尺 , 小 鼠 日 一 尺 , 大 鼠 日 自 倍 , 小 鼠 日 自 半 , 问 何 日 相 逢 ” , 翻 译 过 来 就
是 : 有 五 尺 厚 的 墙 , 两 只 老 鼠 从 墙 的 两 边 相 对 分 别 打 洞 穿 墙 , 大 、 小 鼠 第 一 天 都 进 一 尺 , 以 后
每 天 , 大 鼠 加 倍 , 小 鼠 减 半 , 则 在 第 几 天 两 鼠 相 遇 . 这 个 问 题 体 现 了 古 代 对 数 列 问 题 的 研 究 ,
现 将 墙 的 厚 度 改 为 1 3 0 尺 , 则 在 第 几 天 墙 才 能 被 打 穿 ?
A ? 6 B ? 7 C ? 8 D ? 9
8 ? 设 △ A B C 的 内 角 A , B , C 所 对 的 边 分 别 为 a , b , c , 若 2 a c o s B = c , 则 △ A B C 的 形 状 一 定 是
A ? 直 角 三 角 形 B ? 等 腰 直 角 三 角 形 C ? 等 腰 三 角 形 D ? 等 边 三 角 形
S 4 1 S 8
9 ? 设 S n 是 等 差 数 列 { a n } 的 前 n 项 和 , 若 = , 则 =
S 8 3 S 16
3 3 1 1
A ? B ? C ? D ?
5 1 0 2 5
2
1 0 ? 当 x ∈ R 时 , 不 等 式 k x - k x + 2 > 0 恒 成 立 , 则 k 的 取 值 范 围 是
A ? ( - ∞ , 0 ] ∪ ( 8 , + ∞ ) B ? [ 0 , + ∞ )
C ? ( 0 , 8 ) D ? [ 0 , 8 )
1 1 ? 如 图 , 某 景 区 欲 在 两 山 顶 A , C 之 间 建 缆 车 , 需 要 测 量 两 山 顶 间 的 距
离 . 已 知 山 高 A B =
槡 3 ( k m ) , C D = 3
槡 3 ( k m ) , 在 水 平 面 上 E 处 测 得 山
顶 A 的 仰 角 为 3 0 ° , 山 顶 C 的 仰 角 为 4 5 ° , ∠ B E D = 1 5 0 ° , 则 两 山 顶 A 、
C 之 间 的 距 离 为
A ?
槡 6 3 ( k m ) B ? 5
槡 3 ( k m )
C ?
槡 1 3 ( k m ) D ?
槡 6 6 ( k m )
2 2
1 2 ? 已 知 方 程 x + b x + c = 0 , 在 ( 0 , 2 ) 上 有 两 个 不 同 的 解 , 则 c + 2 ( b + 2 ) c 的 取 值 范 围 是
2 3
A ? ( 0 , 槡 ) B ? ( 0 , ) C ? ( 0 , 1 ) D ? ( 0 , 2 )
2 4 槡
二 、 填 空 题 ( 本 大 题 共 4 小 题 , 每 小 题 4 分 , 共 1 6 分 )
1 3 . 抛 掷 甲 、 乙 两 枚 质 地 均 匀 且 各 面 分 别 标 有 1 , 2 , 3 , 4 , 5 , 6 的 骰 子 , 记 正 面 向 上 的 数 字 分 别 为
x , y , 则 x < y 的 概 率 是 ?
4
1 4 ? 函 数 y = x + + 2 ( x > 0 ) 的 最 小 值 为 .
x + 1
4
1 5 ? 已 知 数 列 { a n } 满 足 a n + 1 = 且 a 1 = 4 , S n 为 数 列 { a n } 的 前 项 和 , 则 S 2020 = .
2 - a n
1 6 ? 在 △ A B C 中 , 已 知 槡 2 a = 4 c o s C +
槡 2 c s i n B , b = 2
槡 2 , 则 △ A B C 面 积 的 最 大 值 是 ?
芜 湖 市 高 一 数 学 试 题 卷 第 2 页 ( 共 6 页 )
三 、 解 答 题 ( 本 大 题 共 5 小 题 , 共 4 8 分 ? 解 答 应 写 出 文 字 说 明 , 证 明 过 程 或 演 算 步 骤 )
1 7 ? ( 本 小 题 满 分 8 分 )
2
已 知 函 数 f ( x ) = x - ( 3 a + 1 ) x + b ?
( 1 ) 当 a = 1 , b = - 5 时 , 解 不 等 式 f ( x ) > 0 ;
2
( 2 ) 当 b = 2 a + 2 a 时 , 解 关 于 x 的 不 等 式 f ( x ) < 0 ( 结 果 用 a 表 示 ) ?
1 8 ? ( 本 小 题 满 分 1 0 分 )
某 城 市 2 0 0 户 居 民 的 月 平 均 用 电 量 ( 单 位 : 度 ) , 以 [ 1 6 0 , 1 8 0 ) , [ 1 8 0 , 2 0 0 ) , [ 2 0 0 , 2 2 0 ) ,
[ 2 2 0 , 2 4 0 ) , [ 2 4 0 , 2 8 0 ) , [ 2 8 0 , 3 0 0 ) 分 组 的 频 率 分 布 直 方 图 如 下 :
( 1 ) 求 直 方 图 中 x 的 值 ;
( 2 ) 在 月 平 均 用 电 量 为 [ 2 2 0 , 2 4 0 ) , [ 2 4 0 , 2 6 0 ) , [ 2 6 0 , 2 8 0 ) 的 三 组 用 户 中 , 用 分 层 抽 样 的
方 法 抽 取 2 0 户 居 民 , 则 月 平 均 用 电 量 在 [ 2 2 0 , 2 4 0 ) 的 用 户 中 应 抽 取 多 少 户 ?
( 3 ) 求 月 平 均 用 电 量 的 中 位 数 和 平 均 数 .
芜 湖 市 高 一 数 学 试 题 卷 第 3 页 ( 共 6 页 )
1 9 ? ( 本 小 题 满 分 1 0 分 ) s i n A - s i n C a - b
在 △ A B C 中 , 内 角 A , B , C 的 对 边 分 别 是 a , b , c , 且 = .
s i n B a + c
( 1 ) 求 角 C 的 大 小 ;
( 2 ) 若 c = 4
槡 3 , 且 A B 边 上 的 中 线 长 为 5 , 求 △ A B C 的 面 积 .
芜 湖 市 高 一 数 学 试 题 卷 第 4 页 ( 共 6 页 )
2 0 . ( 本 小 题 满 分 1 0 分 )
n + 1
2 a n ?
已 知 数 列 { a n } 满 足 a 1 = 1 , a n + 1 = n ( n ∈ N ) ?
a n + 2
n
( 1 ) 2
证 明 : 数 列 { 是 等 差 数 列 , 并 求 数 列 { a n } 的 通 项 公 式 ;
a n }
( 2 ) 设 b n = n ( n + 1 ) a n , 求 数 列 { b n } 的 前 n 项 和 S n .
芜 湖 市 高 一 数 学 试 题 卷 第 5 页 ( 共 6 页 )
2 1 . ( 本 小 题 满 分 1 0 分 )
如 图 , 芜 湖 市 城 乡 规 划 局 将 龙 窝 湖 定 位 为 市 级 滨 江 湿 地 公 园 , 现 准 备 在 湿 地 内 建 造 一 个 观
景 台 P , 已 知 射 线 A B , A C 为 湿 地 两 边 夹 角 为 1 2 0 ° 的 公 路 且 长 度 均 超 过 2 千 米 , 在 两 条 公 路
A B , A C 上 分 别 设 立 游 客 接 送 点 M , N , 从 观 景 台 P 到 M , N 建 造 两 条 观 光 线 路 P M , P N , 测 得
A M = 2 千 米 , A N = 2 千 米 ?
( 1 ) 求 线 段 M N 的 长 度 ;
( 2 ) 若 ∠ M P N = 6 0 ° , 求 两 条 观 光 线 路 P M 与 P N 之 和 的 最 大 值 ?
芜 湖 市 高 一 数 学 试 题 卷 第 6 页 ( 共 6 页 )
20— 202 1 学 年 度 第 二 学 期 芜 湖 市 中 小 学 校 教 育 教 学 质 量 监 控
高一年级数学参考答案及评分标准 ( 必 修 数 学 ③⑤ )
一 、 选择题 ( 本大题共 12 小题 , 每小题 3 分 , 共 36 分 )
题 号 1 2 3 4 5 6 7 8 9 10 11 12
答 案 C A B D B C C C B D B C
二 、 填空题 ( 本大题共 4 个小题 , 每小题 4 分 , 共 16 分 )
5
13 ? 1 4 ? 5 1 5 ? 2 0 2 3 1 6 ? 2 2 + 1 )
1 2
、 ( , )
( 本 小 题 满 分 分 )
( ) , b = - f ( x ) = x - 4 x - = ( x + ) ( )
f ( x ) > 0 - - 1 ) ( 5 , + 3
2 ) a + 2 a f ( x ) = x - ( 3 a + ) x + a + 2 a = x - a ) [ ( a + ) ]
( x ) < 0 x - a ) [ ( a + ) ] 0 5
当 时 2 a > a + , ( a + , 2 a ) 6
当 时 2 a = a + , 7
当 时 2 a < a + , ( 2 a , a + ) 8
1 8 ? 本 小 题 满 分 分 )
( ) 由 直 方 图 的 性 质 可 得
0 . 0 0 2 0 . 0 0 9 5 0 . 0 1 1 0 . 0 1 2 5 0 . 0 0 5 0 . 0 0 2 5 × 2 0 1
: x = . 0 0 7 5 所 以 直 方 图 中 的 值 是 . 0 0 7 5 … … … … … … … … … … … … … 2 分
2 ) 月 平 均 用 电 量 比 例 为 5
所 以 月 平 均 用 电 量 在 2 2 0 2 4 0 2 0 1 0 ? 5
1 0
3 ) ( 0 . 0 0 2 0 . 0 0 9 5 0 . 0 1 1 × 2 0 0 . 4 5 0 . 5 ,
卷 [ 2 2 0 2 4 0 内 , 设 中 位 数 为 ,
( 0 . 0 0 2 0 . 0 0 9 5 0 . 0 1 1 × 2 0 0 . 0 1 2 5 ( a - = 0 . 5
a = . 7
1 7 0 0 . 0 4 1 9 0 0 . 1 9 2 1 0 0 . 2 2 2 3 0 0 . 2 5 2 5 0 0 . 1 5 2 7 0
0 . 1 + 2 9 0 0 . 0 5 9
2 2 5 6 1 0
1 9 ? 1 0
1 ) 由 正 弦 定 理 得 化 简 得 … … … … … … … … … … 分
由 余 弦 定 理 得
芜 湖 市 高 一 数 学 试 题 卷 答 案 第 页 ( 共
π
由 C ∈ ( 0 , π ) 可 得 C = ; … … … … … … … … … … … … … … … … … … … … … 4 分
3
( 2 ) 倍 长 A B 边 上 的 中 线 至 C D , 连 接 D A , 在 △ D A C 中 由 ∠ C A D 的 余 弦 定 理 可 得
2 2
a + b - 1 0 0 1 2 2
c o s ∠ C A D = = - ? a + b + a b = 1 0 0 … … … … … … … … … 8 分
2 a b 2
2 2 2 2 2
又 由 ( 1 ) 知 a + b - c = a b 即 a + b - 4 8 = a b
所 以 a b = 2 6 ,
1 1 3 1 3 3
所 以 S = a b s i n C = × 2 6 × 槡 = 槡 … … … … … … … … … … … … … … 1 0 分
2 2 2 2
2 0 . ( 本 小 题 满 分 1 0 分 )
a n + 1 n n + 1 n
n + 1 a n 2 2 2 2
( 1 ) 由 已 知 可 得 n + 1 = n , 所 以 = + 1 , 即 - = 1 ,
2 a n + 2 a n + 1 a n a n + 1 a n
n
∴ 2
数 列 { 是 公 差 为 1 的 等 差 数 列 , … … … … … … … … … … … … … … … … … … 3 分
a n }
n
2 2
∴ = + ( n - 1 ) · 1 = n + 1 ,
a n a 1
n
2
∴ a n = . … … … … … … … … … … … … … … … … … … … … … … … … … … … … 4 分
n + 1
n
( 2 ) 由 ( 1 ) 知 , b n = n · 2 , … … … … … … … … … … … … … … … … … … … … … … … … 5 分
2 3 n
所 以 S n = 1 · 2 + 2 · 2 + 3 · 2 + … + n · 2 ,
2 3 4 n + 1
2 S n = 1 · 2 + 2 · 2 + 3 · 2 + … + n · 2 ,
2 3 n n + 1 n + 1 n + 1
相 减 得 - S n = 2 + 2 + 2 + … + 2 - n · 2 = 2 - 2 - n · 2 ,
n + 1
∴ S n = ( n - 1 ) 2 + 2 ? … … … … … … … … … … … … … … … … … … … … … … 1 0 分
2 1 . ( 本 小 题 满 分 1 0 分 )
( 1 ) 在 △ A M N 中 , 由 余 弦 定 理 得 ,
2 2 2 2 2 1
M N = A M + A N - 2 A M · A N c o s 1 2 0 ° = 2 + 2 - 2 × 2 × 2 × ( - ) = 1 2 ,
2
所 以 M N = 2
槡 3 千 米 ? … … … … … … … … … … … … … … … … … … … … … … … … 3 分
( 2 ) 设 ∠ P M N = α , 因 为 ∠ M P N = 6 0 ° , 所 以 ∠ P N M = 1 2 0 ° - α ,
M N P M P N
在 △ P M N 中 , 由 正 弦 定 理 得 , = = = 4
s i n ∠ M P N s i n ( 1 2 0 ° - α ) s i n α
所 以 P M = 4 s i n ( 1 2 0 ° - α ) , P N = 4 s i n α … … … … … … … … … … … … … … … … 5 分
3 1
所 以 P M + P N = 4 s i n ( 1 2 0 ° - α ) + 4 s i n α = 4 ( 槡 c o s α + s i n α ) + 4 s i n α
2 2
= 6 s i n α + 2
槡 3 c o s α = 4
槡 3 s i n ( α + 3 0 ° ) , … … … … … … … … … … … … … … … … 8 分
因 为 0 ° < α < 1 2 0 ° , 所 以 3 0 ° < α + 3 0 ° < 1 5 0 ° ,
所 以 当 α + 3 0 ° = 9 0 ° , 即 α = 6 0 ° 时 , P M + P N 取 到 最 大 值 4
槡 3 ?
答 : 两 条 观 光 线 路 距 离 之 和 的 最 大 值 为 4
槡 3 千 米 ? … … … … … … … … … … … 1 0 分
芜 湖 市 高 一 数 学 试 题 卷 答 案 第 2 页 ( 共 2 页 )
同课章节目录
