复习练习卷8(不等式的证明一)-【新教材】2020-2021学年沪教版(2020)高中数学必修第一册(Word含答案)
文档属性
| 名称 | 复习练习卷8(不等式的证明一)-【新教材】2020-2021学年沪教版(2020)高中数学必修第一册(Word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 639.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 00:00:00 | ||
图片预览

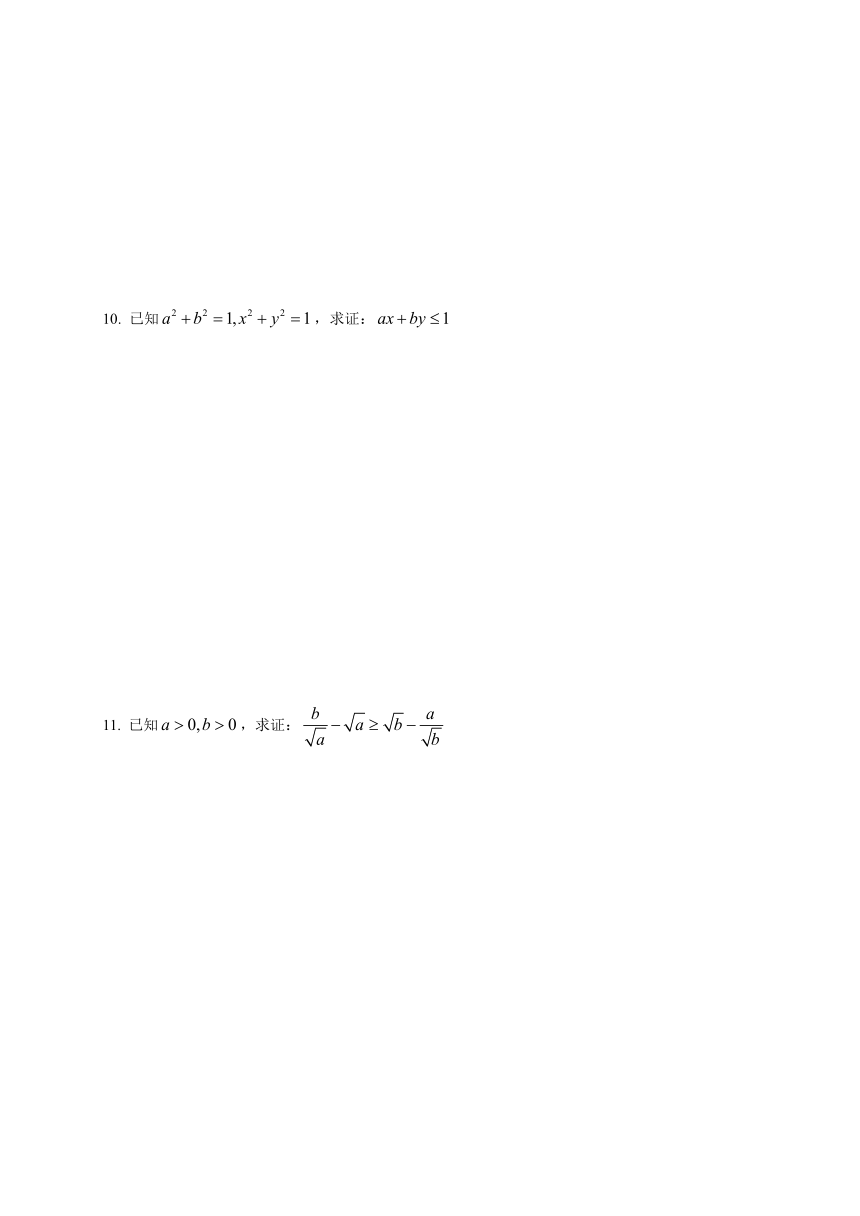
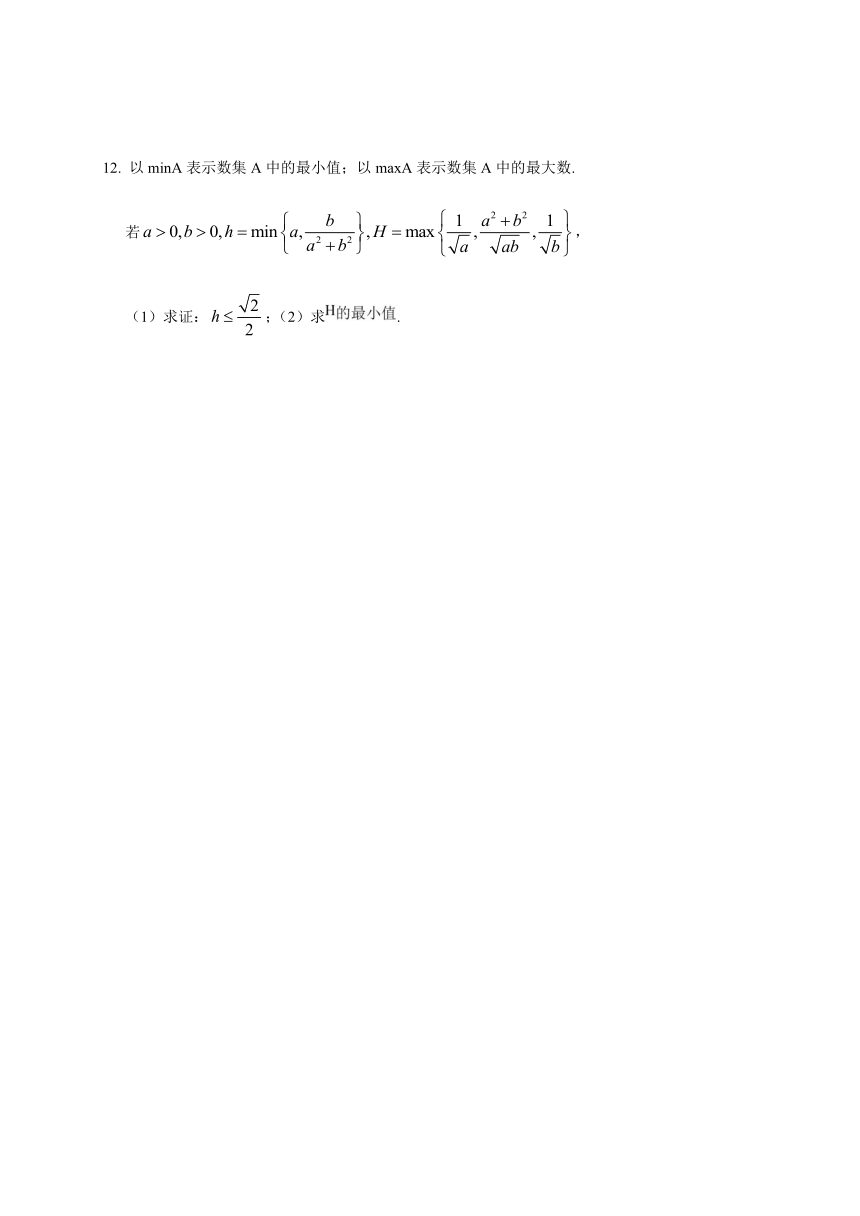
文档简介
2020新版上海高一上数学练习卷8—不等式的证明一
一、填空题
1. 若,则与的大小关系是____________
2. 若,则与的大小关系是____________
3. 若“且”成立,则应满足的条件是____________
4. 若,其中,请用不等号连接:P____________Q
5. 若,若,则b与c的大小关系是____________
二、选择题
6. 若,则( )
A. B. C. D.
7. 若,则“”是“”的( )
A. 充分非必要条件 B. 必要非充分条件
C. 充要条件 D. 既非充分又非必要条件
8. 若,且,则以下不等式中正确的是( )
A. B.
C. D.
三、解答题
9. 已知,求证:
10. 已知,求证:
11. 已知,求证:
12. 以minA表示数集A中的最小值;以maxA表示数集A中的最大数.
若,
(1)求证:;(2)求.
2020新版上海高一上数学练习卷8—不等式的证明一参考答案
一、填空题
1. 2. 3. 或 4. P
一、填空题
1. 若,则与的大小关系是____________
2. 若,则与的大小关系是____________
3. 若“且”成立,则应满足的条件是____________
4. 若,其中,请用不等号连接:P____________Q
5. 若,若,则b与c的大小关系是____________
二、选择题
6. 若,则( )
A. B. C. D.
7. 若,则“”是“”的( )
A. 充分非必要条件 B. 必要非充分条件
C. 充要条件 D. 既非充分又非必要条件
8. 若,且,则以下不等式中正确的是( )
A. B.
C. D.
三、解答题
9. 已知,求证:
10. 已知,求证:
11. 已知,求证:
12. 以minA表示数集A中的最小值;以maxA表示数集A中的最大数.
若,
(1)求证:;(2)求.
2020新版上海高一上数学练习卷8—不等式的证明一参考答案
一、填空题
1. 2. 3. 或 4. P
二、选择题
6. C 7. C 8. A
三、解答题
9. 证明:∵x,y∈R,
∴ x2+4y2+2﹣(2x+4y)=(x﹣1)2+(2y﹣1)2≥0,当且仅当时取等号.
∴ 证明:
10. 证明:
方法一(综合法):
∵2ax≤a2+x2,2by≤b2+y2,∴2(ax+by)≤(a2+b2)+(x2+y2).
又∵a2+b2=1,x2+y2=1,∴2(ax+by)≤2,∴ax+by≤1.
方法二(分析法):
要证ax+by≤1成立,只要证1-(ax+by)≥0,只要证2-2ax-2by≥0,
又∵a2+b2=1,x2+y2=1,∴只要证a2+b2+x2+y2-2ax-2by≥0,
即证(a-x)2+(b-y)2≥0,显然成立.
∴ax+by≤1成立.
11. 证明:
方法一(综合法):
方法二(分析法):
12. (1)证明:∵h=min{a,, ∴0<h≤a,,
∴=,∴.﹣﹣(4分)
(2)∵,,,∴,,,
∴=,当且仅当a=b时取等号
∴. 所以H的最小值为﹣﹣(10分)
