复习练习卷15(幂函数)-【新教材】2020-2021学年沪教版(2020)高中数学必修第一册(Word)
文档属性
| 名称 | 复习练习卷15(幂函数)-【新教材】2020-2021学年沪教版(2020)高中数学必修第一册(Word) |
|
|
| 格式 | docx | ||
| 文件大小 | 168.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 00:00:00 | ||
图片预览

文档简介
2020新版上海高一上数学练习卷15—幂函数
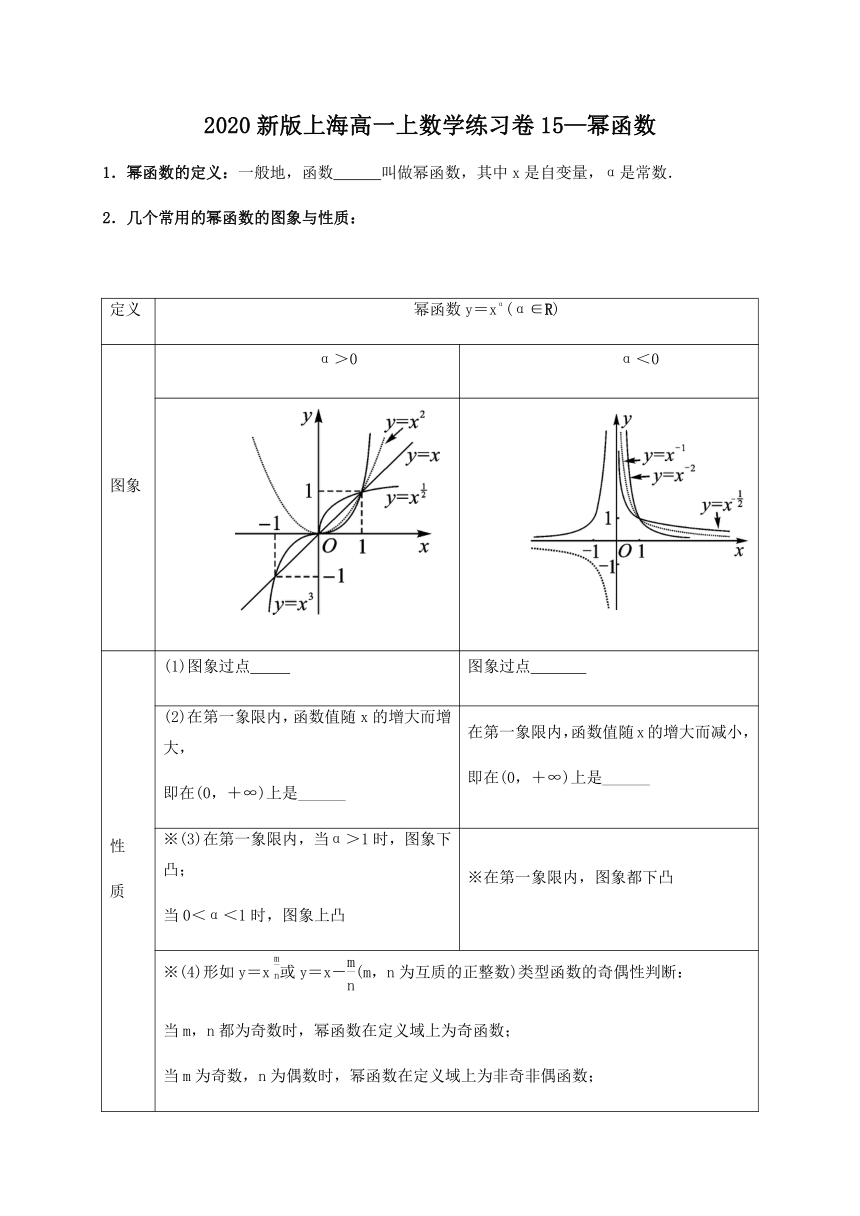
1.幂函数的定义:一般地,函数 叫做幂函数,其中x是自变量,α是常数.
2.几个常用的幂函数的图象与性质:
定义
幂函数y=xα(α∈R)
图象
α>0
α<0
性
质
(1)图象过点
图象过点
(2)在第一象限内,函数值随x的增大而增大,
即在(0,+∞)上是______
在第一象限内,函数值随x的增大而减小,
即在(0,+∞)上是______
※(3)在第一象限内,当α>1时,图象下凸;
当0<α<1时,图象上凸
※在第一象限内,图象都下凸
※(4)形如y=x或y=x-(m,n为互质的正整数)类型函数的奇偶性判断:
当m,n都为奇数时,幂函数在定义域上为奇函数;
当m为奇数,n为偶数时,幂函数在定义域上为非奇非偶函数;
当m为偶数,n为奇数时,幂函数在定义域上为偶函数.
答案:1.y=xα 2.(1)(0,0)和(1,1) (1,1) (2)增函数 减函数
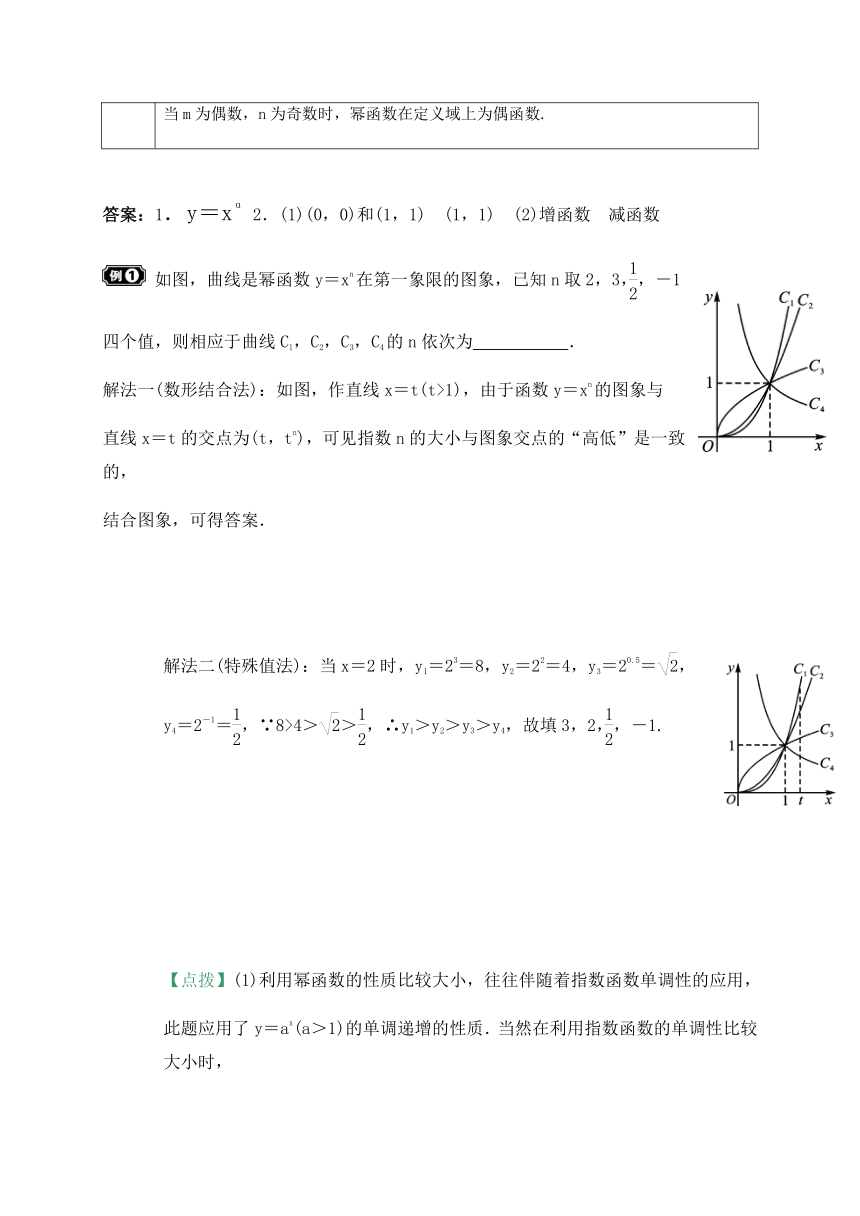
如图,曲线是幂函数y=xn在第一象限的图象,已知n取2,3,,-1
四个值,则相应于曲线C1,C2,C3,C4的n依次为 .
解法一(数形结合法):如图,作直线x=t(t>1),由于函数y=xn的图象与
直线x=t的交点为(t,tn),可见指数n的大小与图象交点的“高低”是一致的,
结合图象,可得答案.
解法二(特殊值法):当x=2时,y1=23=8,y2=22=4,y3=20.5=,
y4=2-1=,∵8>4>>,∴y1>y2>y3>y4,故填3,2,,-1.
【点拨】(1)利用幂函数的性质比较大小,往往伴随着指数函数单调性的应用,
此题应用了y=ax(a>1)的单调递增的性质.当然在利用指数函数的单调性比较大小时,
也会伴随着幂函数单调性质的应用.
(2)当两个幂的底数和指数都不相同时,可以寻找一个中间量,以它作为桥梁,分别构造
指数函数和幂函数,通过比较它们和这个中间量的大小解决问题.
在下列直角坐标系的第一象限内分别画出了函数y=x,y=,y=x2,y=x3,
y=x-1的部分图象,则函数y=false的图象通过的阴影区域是( )
解:函数y=false的图象位于函数y=x与y=x2的图象之间,对比各选项中的阴影区域,
知C正确.故选C.
1.指数函数的图象、性质在应用时,如果底数a的取值范围不确定,则要对其进行分类讨论.
2.比较两个幂的大小,首先要分清是底数相同还是指数相同.如果底数相同,可利用指数函数的单调性;如果指数相同,可转化为底数相同,或利用幂函数的单调性,也可借助函数图象;如果指数不同,底数也不同,则要利用中间量.
3.熟练掌握指数式与对数式的互化,它不仅体现了两者之间的相互关系,而且为对数的计算、化简、证明等问题提供了更多的解题途径.
4.作指数函数y=ax(a>0,且a≠1)和对数函数y=logax(a>0,且a≠1)的图象应分别抓住
三个点,(0,1),(1,a)和,(1,0),(a,1).
5.比较两个对数的大小的基本方法
(1)若底数为同一常数,则由对数函数的单调性直接进行判断;若底数为同一字母,则需对这一字母
进行分类讨论.
(2)若底数不同真数相同,则可先换底再进行比较.
(3)若底数与真数都不同,则常借助1,0等中间量进行比较.
6.幂函数的图象特征与指数的大小关系,大都可通过幂函数的图象与直线x=2或x=的交点纵坐标的大小反映.一般地,在区间(0,1)上,幂函数中指数越大,函数图象越靠近x轴(简记为“指大、
图低”),在区间(1,+∞)上,幂函数中指数越大,图象越远离x轴(不包括幂函数y=x0).
7.幂函数的图象一定会出现在第一象限内,一定不会出现在第四象限,至于是否出现在第二、三
象限内,则要看函数的定义域和奇偶性.函数的图象最多只能同时出现在两个象限内,如果幂函数
的图象与坐标轴相交,则交点一定是原点.
8.判断一个函数是否为指数函数或对数函数或幂函数,一定要根据三种函数定义给出的“标准”形式.
如f(x)=2x2不是指数函数,而f(x)=23x是指数函数,因为f(x)=23x=8x,此时a=8,
同样f(x)=2x+1也不是指数函数,因为f(x)=2x+1=2·2x,不是f(x)=ax(a>0,且a≠1)的形式.
1.幂函数的定义:一般地,函数 叫做幂函数,其中x是自变量,α是常数.
2.几个常用的幂函数的图象与性质:
定义
幂函数y=xα(α∈R)
图象
α>0
α<0
性
质
(1)图象过点
图象过点
(2)在第一象限内,函数值随x的增大而增大,
即在(0,+∞)上是______
在第一象限内,函数值随x的增大而减小,
即在(0,+∞)上是______
※(3)在第一象限内,当α>1时,图象下凸;
当0<α<1时,图象上凸
※在第一象限内,图象都下凸
※(4)形如y=x或y=x-(m,n为互质的正整数)类型函数的奇偶性判断:
当m,n都为奇数时,幂函数在定义域上为奇函数;
当m为奇数,n为偶数时,幂函数在定义域上为非奇非偶函数;
当m为偶数,n为奇数时,幂函数在定义域上为偶函数.
答案:1.y=xα 2.(1)(0,0)和(1,1) (1,1) (2)增函数 减函数
如图,曲线是幂函数y=xn在第一象限的图象,已知n取2,3,,-1
四个值,则相应于曲线C1,C2,C3,C4的n依次为 .
解法一(数形结合法):如图,作直线x=t(t>1),由于函数y=xn的图象与
直线x=t的交点为(t,tn),可见指数n的大小与图象交点的“高低”是一致的,
结合图象,可得答案.
解法二(特殊值法):当x=2时,y1=23=8,y2=22=4,y3=20.5=,
y4=2-1=,∵8>4>>,∴y1>y2>y3>y4,故填3,2,,-1.
【点拨】(1)利用幂函数的性质比较大小,往往伴随着指数函数单调性的应用,
此题应用了y=ax(a>1)的单调递增的性质.当然在利用指数函数的单调性比较大小时,
也会伴随着幂函数单调性质的应用.
(2)当两个幂的底数和指数都不相同时,可以寻找一个中间量,以它作为桥梁,分别构造
指数函数和幂函数,通过比较它们和这个中间量的大小解决问题.
在下列直角坐标系的第一象限内分别画出了函数y=x,y=,y=x2,y=x3,
y=x-1的部分图象,则函数y=false的图象通过的阴影区域是( )
解:函数y=false的图象位于函数y=x与y=x2的图象之间,对比各选项中的阴影区域,
知C正确.故选C.
1.指数函数的图象、性质在应用时,如果底数a的取值范围不确定,则要对其进行分类讨论.
2.比较两个幂的大小,首先要分清是底数相同还是指数相同.如果底数相同,可利用指数函数的单调性;如果指数相同,可转化为底数相同,或利用幂函数的单调性,也可借助函数图象;如果指数不同,底数也不同,则要利用中间量.
3.熟练掌握指数式与对数式的互化,它不仅体现了两者之间的相互关系,而且为对数的计算、化简、证明等问题提供了更多的解题途径.
4.作指数函数y=ax(a>0,且a≠1)和对数函数y=logax(a>0,且a≠1)的图象应分别抓住
三个点,(0,1),(1,a)和,(1,0),(a,1).
5.比较两个对数的大小的基本方法
(1)若底数为同一常数,则由对数函数的单调性直接进行判断;若底数为同一字母,则需对这一字母
进行分类讨论.
(2)若底数不同真数相同,则可先换底再进行比较.
(3)若底数与真数都不同,则常借助1,0等中间量进行比较.
6.幂函数的图象特征与指数的大小关系,大都可通过幂函数的图象与直线x=2或x=的交点纵坐标的大小反映.一般地,在区间(0,1)上,幂函数中指数越大,函数图象越靠近x轴(简记为“指大、
图低”),在区间(1,+∞)上,幂函数中指数越大,图象越远离x轴(不包括幂函数y=x0).
7.幂函数的图象一定会出现在第一象限内,一定不会出现在第四象限,至于是否出现在第二、三
象限内,则要看函数的定义域和奇偶性.函数的图象最多只能同时出现在两个象限内,如果幂函数
的图象与坐标轴相交,则交点一定是原点.
8.判断一个函数是否为指数函数或对数函数或幂函数,一定要根据三种函数定义给出的“标准”形式.
如f(x)=2x2不是指数函数,而f(x)=23x是指数函数,因为f(x)=23x=8x,此时a=8,
同样f(x)=2x+1也不是指数函数,因为f(x)=2x+1=2·2x,不是f(x)=ax(a>0,且a≠1)的形式.
