复习练习卷16(指数函数)-【新教材】2020-2021学年沪教版(2020)高中数学必修第一册(Word含答案)
文档属性
| 名称 | 复习练习卷16(指数函数)-【新教材】2020-2021学年沪教版(2020)高中数学必修第一册(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 135.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 12:02:00 | ||
图片预览


文档简介
2020新版上海高一上数学复习卷16—指数函数
指数函数的图象及性质:
定义
一般地,函数y=ax(a>0,且a≠1) 叫做指数函数
图
象
a>1
0<a<1
定义域
__________
值域
__________
性质
过定点_____________
在R上是______
在R上是______
答案:R (0,+∞) (0,1) 增函数 减函数
类型一 指数型复合函数的定义域和值域
求下列函数的定义域和值域.
(1)y=; (2)y=;(3)y=false.
解:(1)定义域为R.因为-|x+1|≤0,所以y=≥=1,所以值域为[1,+∞).
(2)定义域为R.又因为y==1-,而0<<1,所以-1<-<0,
则0<y<1,所以值域为(0,1).
(3)令-x2-3x+4≥0,解得-4≤x≤1,所以函数y=false的定义域为[-4,1].
设u=(-4≤x≤1),易得u在x=-时取得最大值,
在x=-4或1时取得最小值0,即0≤u≤.所以函数y=2u的值域为,
即函数y=false的值域为[1,4].
【点拨】指数函数y=ax(a>0,a≠1)的定义域为R,所以y=af(x)的定义域与f(x)的定义域相同;值域则要用其单调性来求,复合函数的单调性要注意“同增异减”的原则.
求下列函数的定义域和值域.
(1)y=8; (2)y=4x+2x+1+1; (3)y=.
解:(1) 因为2x-1≠0,所以x≠,所以原函数的定义域是.
令t=,则t∈R且t≠0,所以由y=8t(t∈R,t≠0)得y>0且y≠1.
所以,原函数的值域是{y|y>0且y≠1}.
(2) 定义域为R,因为y=4x+2x+1+1=(2x)2+2·2x+1=(2x+1)2,且2x>0.
所以y=4x+2x+1+1的值域为{y|y>1}.
(3)设u=x2-6x+17,由于函数u=x2-6x+17的定义域是(-∞,+∞),
故y=的定义域为(-∞,+∞).又函数u=x2-6x+17=(x-3)2+8≥8,所以≤,又>0,故原函数的值域为.
类型二 指数函数的图象及其应用
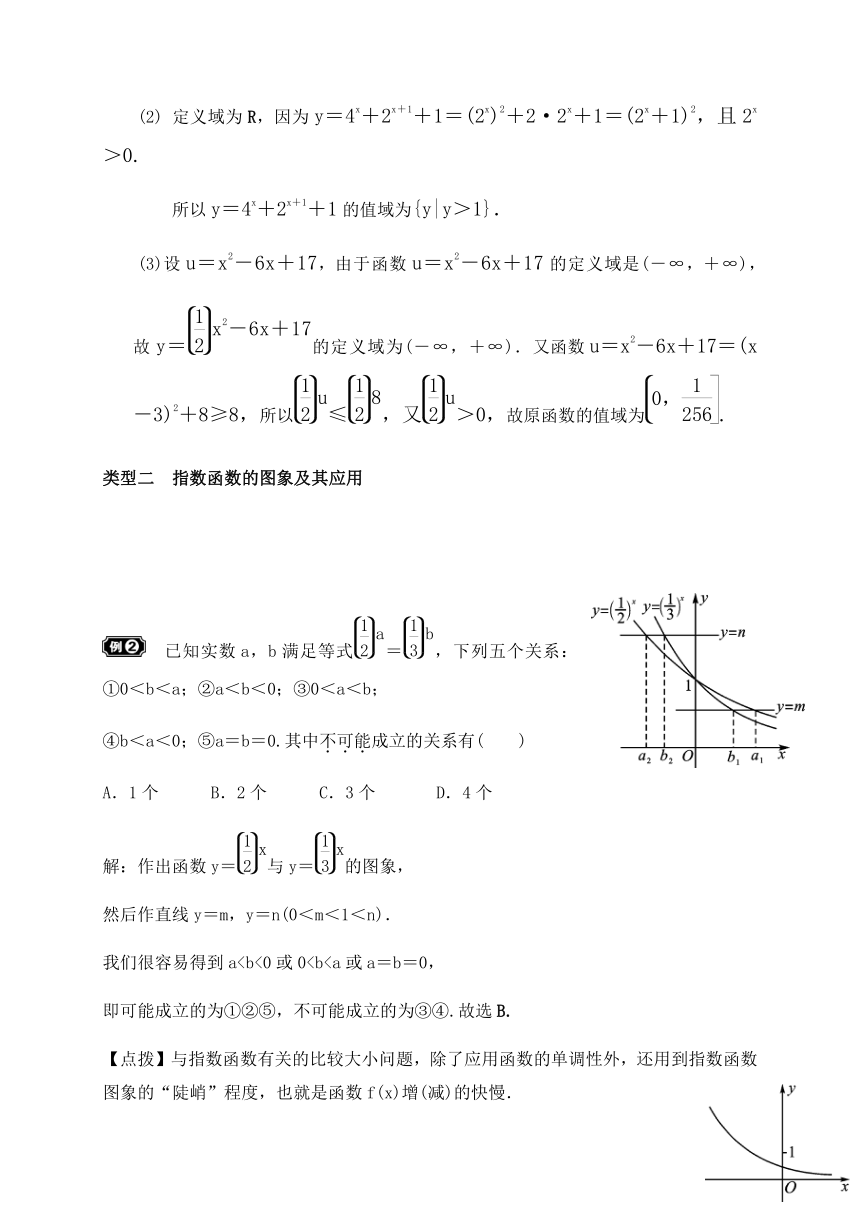
已知实数a,b满足等式=,下列五个关系:①0<b<a;②a<b<0;③0<a<b;
④b<a<0;⑤a=b=0.其中不可能成立的关系有( )
A.1个 B.2个 C.3个 D.4个
解:作出函数y=与y=的图象,
然后作直线y=m,y=n(0<m<1<n).
我们很容易得到a即可能成立的为①②⑤,不可能成立的为③④.故选B.
【点拨】与指数函数有关的比较大小问题,除了应用函数的单调性外,还用到指数函数图象的“陡峭”程度,也就是函数f(x)增(减)的快慢.
函数f(x)=ax-b的图象如图所示,
其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0 B.a>1,b>0
C.0<a<1,b>0 D.0<a<1,b<0
解:由图象知f(x)是减函数,∴0<a<1,又由图象在y轴的截距小于1可知a-b<1,即-b>0,
∴b<0.故选D.
类型三 指数函数的综合问题
设函数f(x)=
(1)若a=1,则f(x)的最小值为________;
(2)若(x)恰有2个零点,则实数a的取值范围是________.
解:(1)a=1时,f(x)=
当x<1时,f(x)∈(-1,1),f(x)无最小值;
当x≥1时,f(x)在为减函数,在为增函数,
当x=时,f(x)取得最小值为-1.
(2)①若函数g(x)=2x-a在x<1时与x轴有一个交点,则a>0,
并且当x=1时,g(1)=2-a>0,则0此时函数h(x)=4(x-a)(x-2a)与x轴只有一个交点,
所以2a≥1且a<1,则≤a<1.综合得≤a<1.
②若函数g(x)=2x-a与x轴有无交点,则函数h(x)=4(x-a)(x-2a)与x轴有两个交点.
当a≤0时,g(x)与x轴无交点,h(x)=4(x-a)(x-2a)在[1,+∞)与x轴也无交点,不合题意;
当g(1)=2-a≤0时,a≥2,h(x)与x轴有两个交点,其横坐标为x=a和x=2a,
由于a≥2,两交点横坐标均满足x≥1,符合题意.
综合①②可得a的取值范围为≤a<1或a≥2.故填-1;∪[2,+∞).
【点拨】解决指数函数的综合问题,首先要熟练掌握指数函数的基本性质,如函数值恒正,
在R上单调,过定点等.本题是指数函数与二次函数的综合问题,由于涉及分段函数的零点个数,
故以分段函数在各段上的零点个数为标准,借助函数图象,分类讨论求解.
已知函数f(x)=2x-.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
解:(1)当x<0时,f(x)=0;当x≥0时,f(x)=2x-.
由条件可知2x-=2,即22x-2·2x-1=0,解得2x=1±.
∵2x>0,∴2x=1+,即x=log2(1+).
(2)当t∈[1,2]时,2t+m≥0,∵2t>0,两边同乘以2t,
即得m(22t-1)≥-(24t-1).∵22t-1>0,∴m≥-(22t+1).
∵t∈[1,2],∴-(1+22t)∈[-17,-5],故m的取值范围是[-5,+∞).
指数函数的图象及性质:
定义
一般地,函数y=ax(a>0,且a≠1) 叫做指数函数
图
象
a>1
0<a<1
定义域
__________
值域
__________
性质
过定点_____________
在R上是______
在R上是______
答案:R (0,+∞) (0,1) 增函数 减函数
类型一 指数型复合函数的定义域和值域
求下列函数的定义域和值域.
(1)y=; (2)y=;(3)y=false.
解:(1)定义域为R.因为-|x+1|≤0,所以y=≥=1,所以值域为[1,+∞).
(2)定义域为R.又因为y==1-,而0<<1,所以-1<-<0,
则0<y<1,所以值域为(0,1).
(3)令-x2-3x+4≥0,解得-4≤x≤1,所以函数y=false的定义域为[-4,1].
设u=(-4≤x≤1),易得u在x=-时取得最大值,
在x=-4或1时取得最小值0,即0≤u≤.所以函数y=2u的值域为,
即函数y=false的值域为[1,4].
【点拨】指数函数y=ax(a>0,a≠1)的定义域为R,所以y=af(x)的定义域与f(x)的定义域相同;值域则要用其单调性来求,复合函数的单调性要注意“同增异减”的原则.
求下列函数的定义域和值域.
(1)y=8; (2)y=4x+2x+1+1; (3)y=.
解:(1) 因为2x-1≠0,所以x≠,所以原函数的定义域是.
令t=,则t∈R且t≠0,所以由y=8t(t∈R,t≠0)得y>0且y≠1.
所以,原函数的值域是{y|y>0且y≠1}.
(2) 定义域为R,因为y=4x+2x+1+1=(2x)2+2·2x+1=(2x+1)2,且2x>0.
所以y=4x+2x+1+1的值域为{y|y>1}.
(3)设u=x2-6x+17,由于函数u=x2-6x+17的定义域是(-∞,+∞),
故y=的定义域为(-∞,+∞).又函数u=x2-6x+17=(x-3)2+8≥8,所以≤,又>0,故原函数的值域为.
类型二 指数函数的图象及其应用
已知实数a,b满足等式=,下列五个关系:①0<b<a;②a<b<0;③0<a<b;
④b<a<0;⑤a=b=0.其中不可能成立的关系有( )
A.1个 B.2个 C.3个 D.4个
解:作出函数y=与y=的图象,
然后作直线y=m,y=n(0<m<1<n).
我们很容易得到a
【点拨】与指数函数有关的比较大小问题,除了应用函数的单调性外,还用到指数函数图象的“陡峭”程度,也就是函数f(x)增(减)的快慢.
函数f(x)=ax-b的图象如图所示,
其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0 B.a>1,b>0
C.0<a<1,b>0 D.0<a<1,b<0
解:由图象知f(x)是减函数,∴0<a<1,又由图象在y轴的截距小于1可知a-b<1,即-b>0,
∴b<0.故选D.
类型三 指数函数的综合问题
设函数f(x)=
(1)若a=1,则f(x)的最小值为________;
(2)若(x)恰有2个零点,则实数a的取值范围是________.
解:(1)a=1时,f(x)=
当x<1时,f(x)∈(-1,1),f(x)无最小值;
当x≥1时,f(x)在为减函数,在为增函数,
当x=时,f(x)取得最小值为-1.
(2)①若函数g(x)=2x-a在x<1时与x轴有一个交点,则a>0,
并且当x=1时,g(1)=2-a>0,则0
所以2a≥1且a<1,则≤a<1.综合得≤a<1.
②若函数g(x)=2x-a与x轴有无交点,则函数h(x)=4(x-a)(x-2a)与x轴有两个交点.
当a≤0时,g(x)与x轴无交点,h(x)=4(x-a)(x-2a)在[1,+∞)与x轴也无交点,不合题意;
当g(1)=2-a≤0时,a≥2,h(x)与x轴有两个交点,其横坐标为x=a和x=2a,
由于a≥2,两交点横坐标均满足x≥1,符合题意.
综合①②可得a的取值范围为≤a<1或a≥2.故填-1;∪[2,+∞).
【点拨】解决指数函数的综合问题,首先要熟练掌握指数函数的基本性质,如函数值恒正,
在R上单调,过定点等.本题是指数函数与二次函数的综合问题,由于涉及分段函数的零点个数,
故以分段函数在各段上的零点个数为标准,借助函数图象,分类讨论求解.
已知函数f(x)=2x-.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
解:(1)当x<0时,f(x)=0;当x≥0时,f(x)=2x-.
由条件可知2x-=2,即22x-2·2x-1=0,解得2x=1±.
∵2x>0,∴2x=1+,即x=log2(1+).
(2)当t∈[1,2]时,2t+m≥0,∵2t>0,两边同乘以2t,
即得m(22t-1)≥-(24t-1).∵22t-1>0,∴m≥-(22t+1).
∵t∈[1,2],∴-(1+22t)∈[-17,-5],故m的取值范围是[-5,+∞).
