1.3.1 函数的单调性与导数-人教A版高中数学选修2-2课时练习(Word含答案)
文档属性
| 名称 | 1.3.1 函数的单调性与导数-人教A版高中数学选修2-2课时练习(Word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 261.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 12:16:19 | ||
图片预览

文档简介
高二年级(数学)学科习题卷
函数的单调性与导数
编号:080
选择题:
1.函数的单调递增区间是( )
A. B. C. D.
2.函数在区间上单调递增,则实数的取值范围是( )
A. B. C. D.
3.函数的图象如图,则导函数的图象可能是( )
4.函数的单调递增区间是( )
A. B. C. D.
5.若函数在其定义域内的一个子区间内不是单调函数,则实数
的取值范围是( )
A. B. C. D.
6.函数为上增函数的一个充分不必要条件是( )
A. B. C. D.
7.若,则( )
A. B. C. D.
8.若函数在区间内是增函数,则实数的取值范围是( )
A. B. C. D.
9.函数在上单调递增,则实数的取值范围是( )
A. B. C. D.
10.函数的单调递增区间是( )
A. B. C. D.
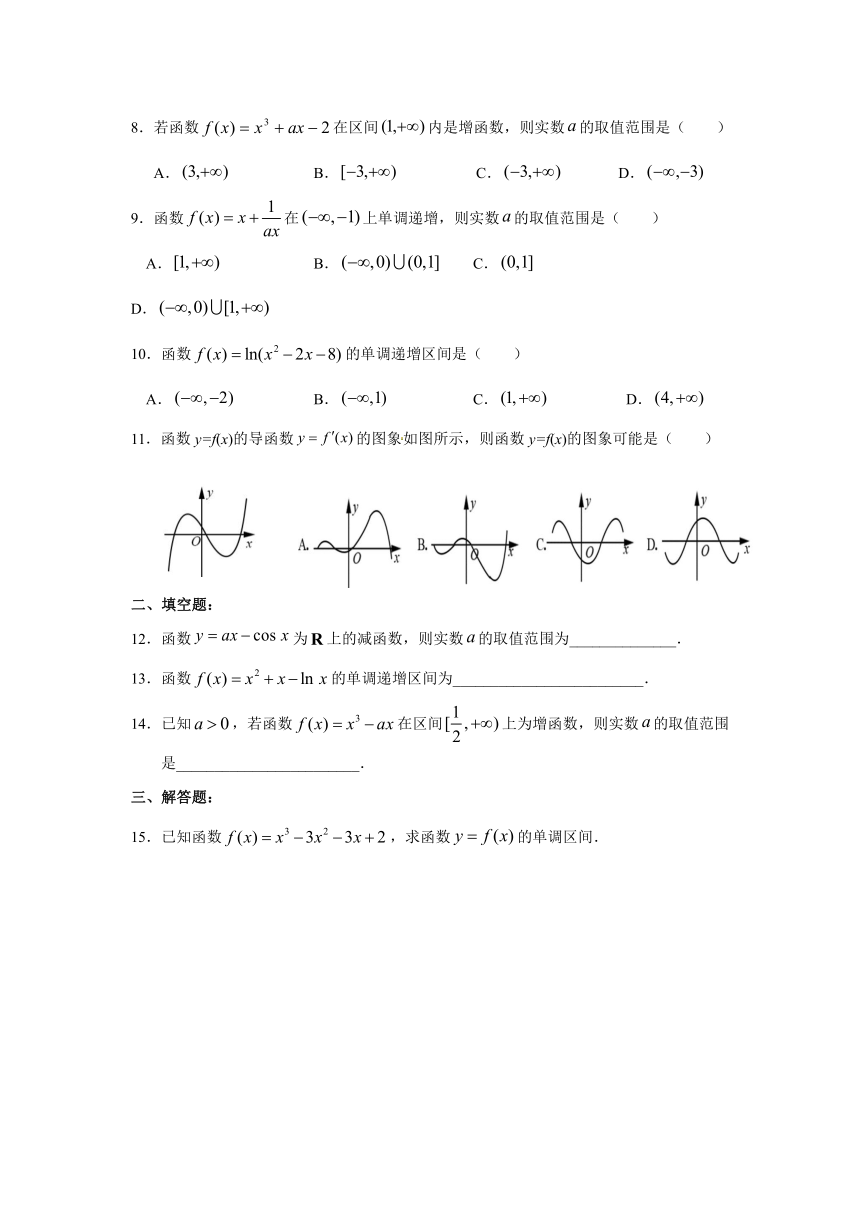
11.函数y=f(x)的导函数的图象如图所示,则函数y=f(x)的图象可能是( )
二、填空题:
12.函数为上的减函数,则实数的取值范围为______________.
13.函数的单调递增区间为_________________________.
14.已知,若函数在区间上为增函数,则实数的取值范围
是________________________.
三、解答题:
15.已知函数,求函数的单调区间.
16.已知函数,.
(1)当时,求曲线在点处的切线方程;
(2)若函数在区间上是减函数,求实数的取值范围.
17.已知函数.
(1)若,求函数的图象在点处的切线方程;
(2)讨论函数的单调区间.
18.(1)已知函数,讨论的单调性.
(2)设函数,讨论的单调性.
(3)已知函数,讨论的单调性.
选择题:
1-5CDCDB 6-11BBBDD D
填空题
12(.-∞,-1) 13.(1/2,+∞) 14(0,3/4]
解答题
15. 由f(x)=x3-3x2-3x+2,所以f′(x)=3x2-6x-3由f′(x)》0知:x<1-根号2或x>1+根号2时;由f′(x)<0知:1-根号2<或x<1+根号2.
16.略17.略
18. (1)f(x)=ex(ex-a)-a2x,
∴f′(x)=2e2x-aex-a2=(2ex+a)(ex-a),
①当a=0时,f′(x)>0恒成立,
∴f(x)在R上单调递增,
②当a>0时,2ex+a>0,令f′(x)=0,解得x=lna,
当x当x>lna时,f′(x)>0,函数f(x)单调递增,
③当a<0时,ex-a>0,令f′(x)=0,解得x=ln(-a/2)
当x当x>ln(- a/2)时,f′(x)>0,函数f(x)单调递增,
综上所述,当a=0时,f(x)在R上单调递增,
当a>0时,f(x)在(-∞,lna)上单调递减,在(lna,+∞)上单调递增,
当a<0时,f(x)在(-∞,ln(- a/2)上单调递减,在(ln(- a/2),+∞)上单调递增,
(3) x>0
f(x)=lnx+ax?-(2a+1)x
f'(x)=1/x+2ax-(2a+1)
f'(x)=[2ax?-(2a+1)x+1]/x
由于1/x>0
讨论2ax?-(2a+1)x+1的即可
f'(x)=0有极值
2ax?-(2a+1)x+1=0
x=(2a+1±√(4a?+4a+1-8a)]/4a
x=2a+1±|2a-1|
x=1/(2a)或x=1
(一)a>0时,△≥0
①a∈(?,+∞)时,x∈(1/(2a),1),
f(x)单调↓,x∈(0,1/(2a))U(1,+∞)单调↑
②a∈(-∞,?]时,x∈(1,1/(2a)),
f(x)单调↓,,x∈(0,1)U(1/(2a),+∞)单调↑
函数的单调性与导数
编号:080
选择题:
1.函数的单调递增区间是( )
A. B. C. D.
2.函数在区间上单调递增,则实数的取值范围是( )
A. B. C. D.
3.函数的图象如图,则导函数的图象可能是( )
4.函数的单调递增区间是( )
A. B. C. D.
5.若函数在其定义域内的一个子区间内不是单调函数,则实数
的取值范围是( )
A. B. C. D.
6.函数为上增函数的一个充分不必要条件是( )
A. B. C. D.
7.若,则( )
A. B. C. D.
8.若函数在区间内是增函数,则实数的取值范围是( )
A. B. C. D.
9.函数在上单调递增,则实数的取值范围是( )
A. B. C. D.
10.函数的单调递增区间是( )
A. B. C. D.
11.函数y=f(x)的导函数的图象如图所示,则函数y=f(x)的图象可能是( )
二、填空题:
12.函数为上的减函数,则实数的取值范围为______________.
13.函数的单调递增区间为_________________________.
14.已知,若函数在区间上为增函数,则实数的取值范围
是________________________.
三、解答题:
15.已知函数,求函数的单调区间.
16.已知函数,.
(1)当时,求曲线在点处的切线方程;
(2)若函数在区间上是减函数,求实数的取值范围.
17.已知函数.
(1)若,求函数的图象在点处的切线方程;
(2)讨论函数的单调区间.
18.(1)已知函数,讨论的单调性.
(2)设函数,讨论的单调性.
(3)已知函数,讨论的单调性.
选择题:
1-5CDCDB 6-11BBBDD D
填空题
12(.-∞,-1) 13.(1/2,+∞) 14(0,3/4]
解答题
15. 由f(x)=x3-3x2-3x+2,所以f′(x)=3x2-6x-3由f′(x)》0知:x<1-根号2或x>1+根号2时;由f′(x)<0知:1-根号2<或x<1+根号2.
16.略17.略
18. (1)f(x)=ex(ex-a)-a2x,
∴f′(x)=2e2x-aex-a2=(2ex+a)(ex-a),
①当a=0时,f′(x)>0恒成立,
∴f(x)在R上单调递增,
②当a>0时,2ex+a>0,令f′(x)=0,解得x=lna,
当x
③当a<0时,ex-a>0,令f′(x)=0,解得x=ln(-a/2)
当x
综上所述,当a=0时,f(x)在R上单调递增,
当a>0时,f(x)在(-∞,lna)上单调递减,在(lna,+∞)上单调递增,
当a<0时,f(x)在(-∞,ln(- a/2)上单调递减,在(ln(- a/2),+∞)上单调递增,
(3) x>0
f(x)=lnx+ax?-(2a+1)x
f'(x)=1/x+2ax-(2a+1)
f'(x)=[2ax?-(2a+1)x+1]/x
由于1/x>0
讨论2ax?-(2a+1)x+1的即可
f'(x)=0有极值
2ax?-(2a+1)x+1=0
x=(2a+1±√(4a?+4a+1-8a)]/4a
x=2a+1±|2a-1|
x=1/(2a)或x=1
(一)a>0时,△≥0
①a∈(?,+∞)时,x∈(1/(2a),1),
f(x)单调↓,x∈(0,1/(2a))U(1,+∞)单调↑
②a∈(-∞,?]时,x∈(1,1/(2a)),
f(x)单调↓,,x∈(0,1)U(1/(2a),+∞)单调↑
