北师大版八年级数学上册第一章勾股定理本章小结与复习作业课件(24张ppt)
文档属性
| 名称 | 北师大版八年级数学上册第一章勾股定理本章小结与复习作业课件(24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 20:56:02 | ||
图片预览


文档简介
(共24张PPT)
本章小结与复习
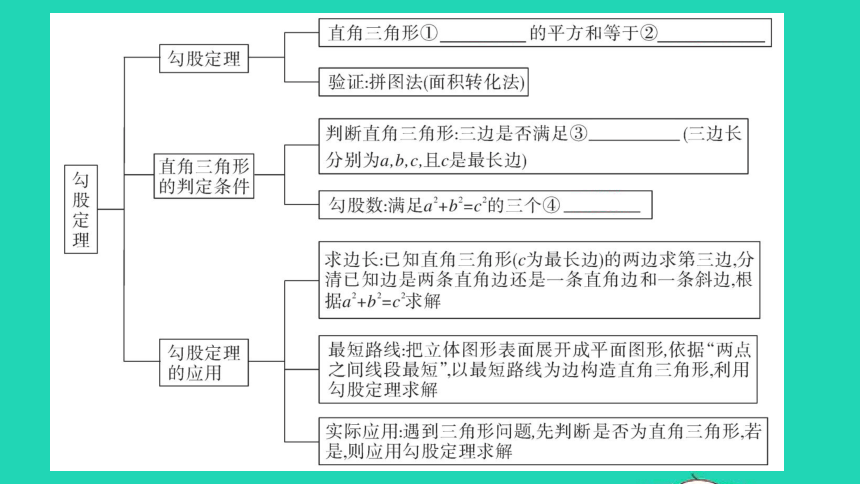
直角三角形①两直角边的平方和等于②斜边的平方
勾股定理
验证:拼图法面积转化法)
判断直角三角形:三边是否满足③a+b=c(三边长
直角三角形
分别为a,b,c,且c是最长边)
勾股定理
的判定条件
勾股数满足a+b=c的三个④正整数
求边长:已知直角三角形(c为最长边)的两边求第三边,分
清已知边是两条直角边还是一条直角边和一条斜边根
据a2+b2=c2求解
勾股定理
最短路线:把立体图形表面展开成平面图形,依据“两点
的应用
之间线段最短”,以最短路线为边构造直角三角形利用
勾股定理求解
实际应用:遇到三角形问题先判断是否为直角三角形,若
是,则应用勾股定理求解
考点整合训练
◆考点一勾股定理及其验证
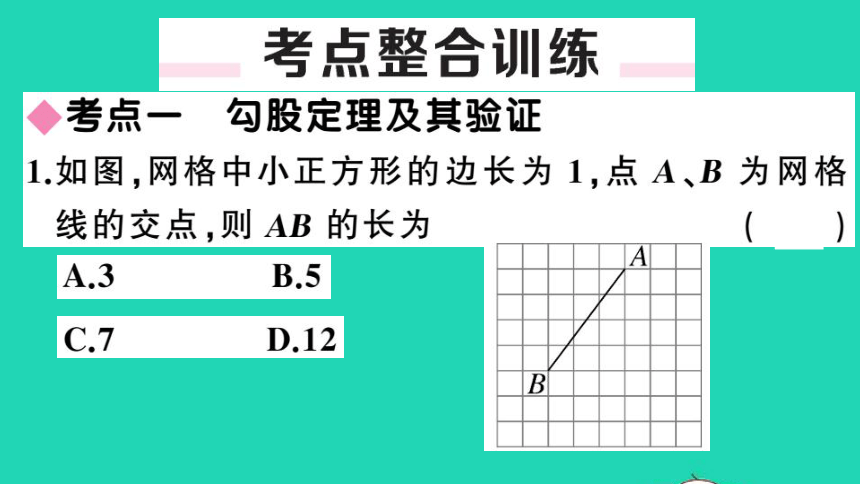
1.如图,网格中小正方形的边长为1,点A、B为网格
线的交点,则AB的长为
B
A
B
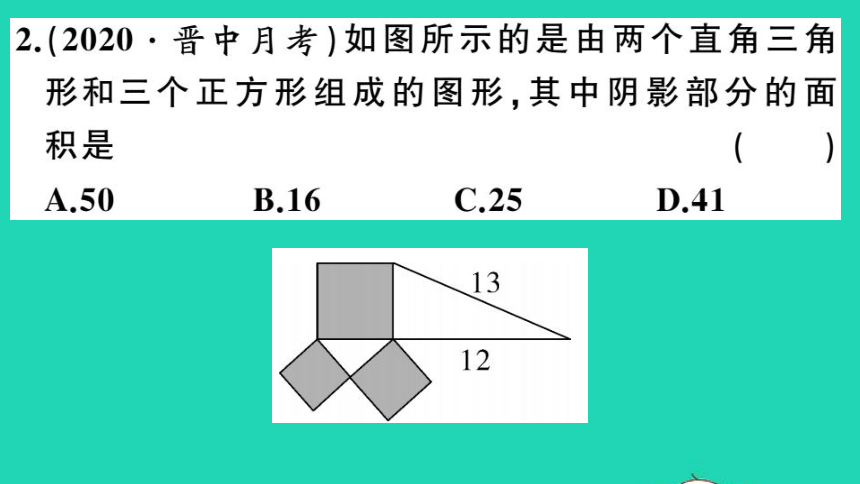
2.(2020·晋中月考)如图所示的是由两个直角三角
形和三个正方形组成的图形,其中阴影部分的面
积是
(A
A.50
B.16
C.25
13
12
3如图是由4个全等的直角三角形与1个正方形镶
嵌而成的正方形图案,已知大正方形的面积为49,
N正方形的面积为4若用x,y表示直角三角形的
两直角边长(x>y),则下列结论错误的是(D
A,x2+y2=49
Bx-y=2
C.2xy+4=49
Dxty=9
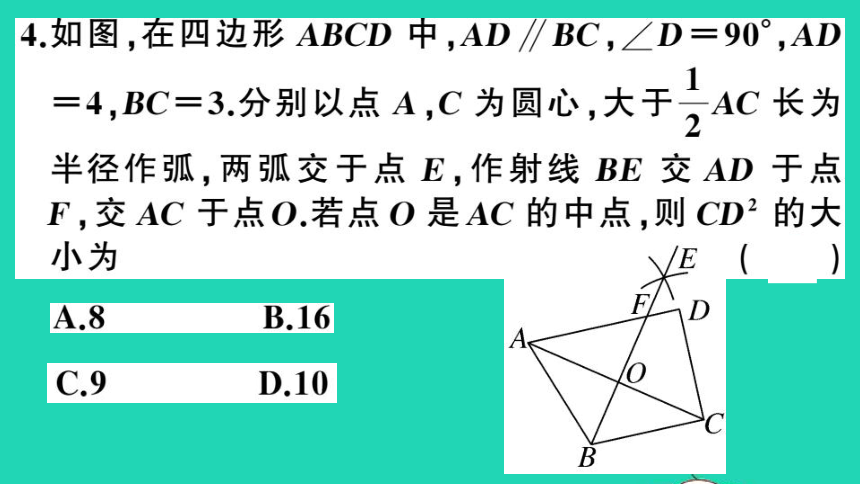
4如图,在四边形ABCD中,AD∥BC,∠D=90°,AD
BC=3分别以点A,C为圆心,大于AC长为
半径作弧,两弧交于点E,作射线BE交AD于点
F,交AC于点O若点O是AC的中点,则CD2的大
小为
(A
ED
C
B
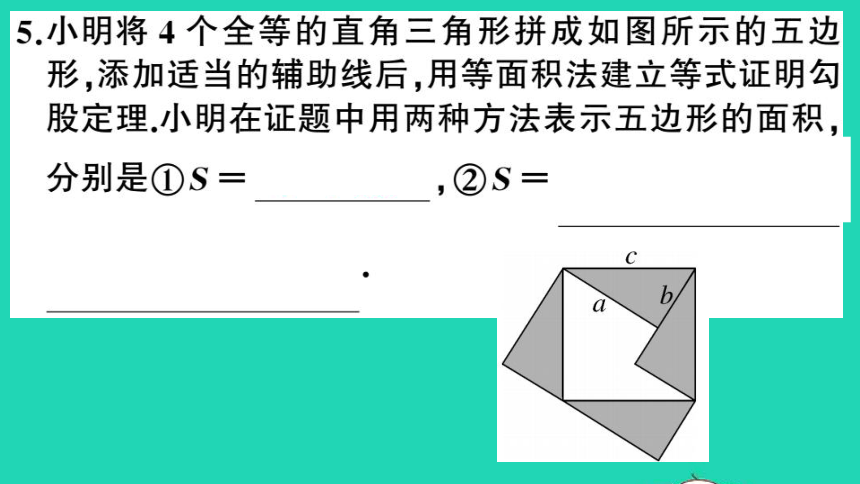
5.小明将4个全等的直角三角形拼成如图所示的五边
形,添加适当的辅助线后,用等面积法建立等式证明勾
股定理.小明在证题中用两种方法表示五边形的面积
分别是①S=c2+ab,②S=a2+b2+ab或
(a+b)2+c2
2
C
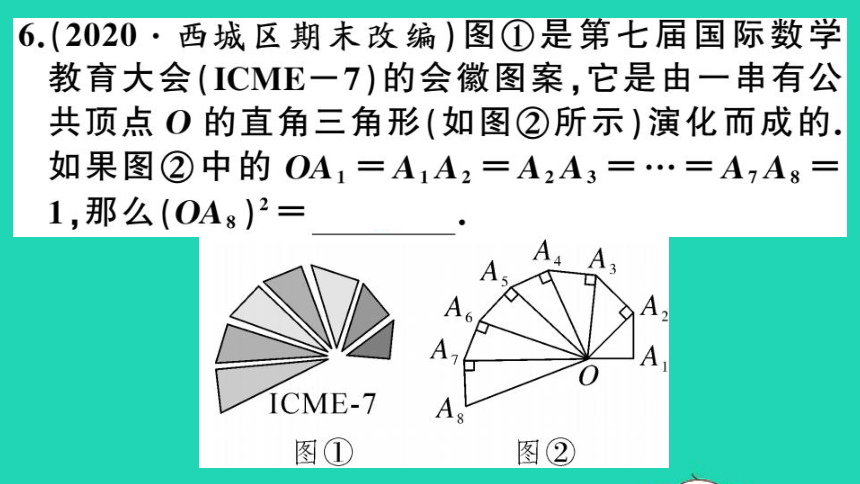
6.、(2020·西城区期末改编)图①是第七届国际数学
教育大会(ICME-7的会徽图案,它是由一串有公
共顶点O的直角三角形(如图②所示)演化而成的
如果图②中的OA1=A1A2=A2A3=…=AA8
1,那么(OAs)2=8
A
A
ICME-7
A
图①
图②
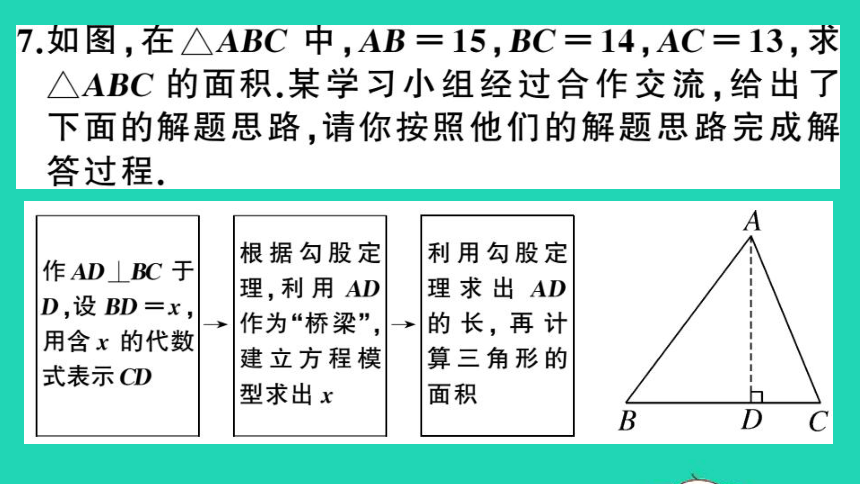
7如图,在△ABC中,AB=15,BC=14,AC=13,求
△ABC的面积.某学习小组经过合作交流,给出了
下面的解题思路,请你按照他们的解题思路完成解
答过程
本章小结与复习
直角三角形①两直角边的平方和等于②斜边的平方
勾股定理
验证:拼图法面积转化法)
判断直角三角形:三边是否满足③a+b=c(三边长
直角三角形
分别为a,b,c,且c是最长边)
勾股定理
的判定条件
勾股数满足a+b=c的三个④正整数
求边长:已知直角三角形(c为最长边)的两边求第三边,分
清已知边是两条直角边还是一条直角边和一条斜边根
据a2+b2=c2求解
勾股定理
最短路线:把立体图形表面展开成平面图形,依据“两点
的应用
之间线段最短”,以最短路线为边构造直角三角形利用
勾股定理求解
实际应用:遇到三角形问题先判断是否为直角三角形,若
是,则应用勾股定理求解
考点整合训练
◆考点一勾股定理及其验证
1.如图,网格中小正方形的边长为1,点A、B为网格
线的交点,则AB的长为
B
A
B
2.(2020·晋中月考)如图所示的是由两个直角三角
形和三个正方形组成的图形,其中阴影部分的面
积是
(A
A.50
B.16
C.25
13
12
3如图是由4个全等的直角三角形与1个正方形镶
嵌而成的正方形图案,已知大正方形的面积为49,
N正方形的面积为4若用x,y表示直角三角形的
两直角边长(x>y),则下列结论错误的是(D
A,x2+y2=49
Bx-y=2
C.2xy+4=49
Dxty=9
4如图,在四边形ABCD中,AD∥BC,∠D=90°,AD
BC=3分别以点A,C为圆心,大于AC长为
半径作弧,两弧交于点E,作射线BE交AD于点
F,交AC于点O若点O是AC的中点,则CD2的大
小为
(A
ED
C
B
5.小明将4个全等的直角三角形拼成如图所示的五边
形,添加适当的辅助线后,用等面积法建立等式证明勾
股定理.小明在证题中用两种方法表示五边形的面积
分别是①S=c2+ab,②S=a2+b2+ab或
(a+b)2+c2
2
C
6.、(2020·西城区期末改编)图①是第七届国际数学
教育大会(ICME-7的会徽图案,它是由一串有公
共顶点O的直角三角形(如图②所示)演化而成的
如果图②中的OA1=A1A2=A2A3=…=AA8
1,那么(OAs)2=8
A
A
ICME-7
A
图①
图②
7如图,在△ABC中,AB=15,BC=14,AC=13,求
△ABC的面积.某学习小组经过合作交流,给出了
下面的解题思路,请你按照他们的解题思路完成解
答过程
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
