均值不等式(最终定稿)[1]1
文档属性
| 名称 | 均值不等式(最终定稿)[1]1 |

|
|
| 格式 | zip | ||
| 文件大小 | 241.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-17 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
3.4 基本不等式:
华南师大附中 曲政
ICM2002会标
如图,这是在北京召开的第22届国际数学家大会会标.会标根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车,代表中国人民热情好客。
a
b
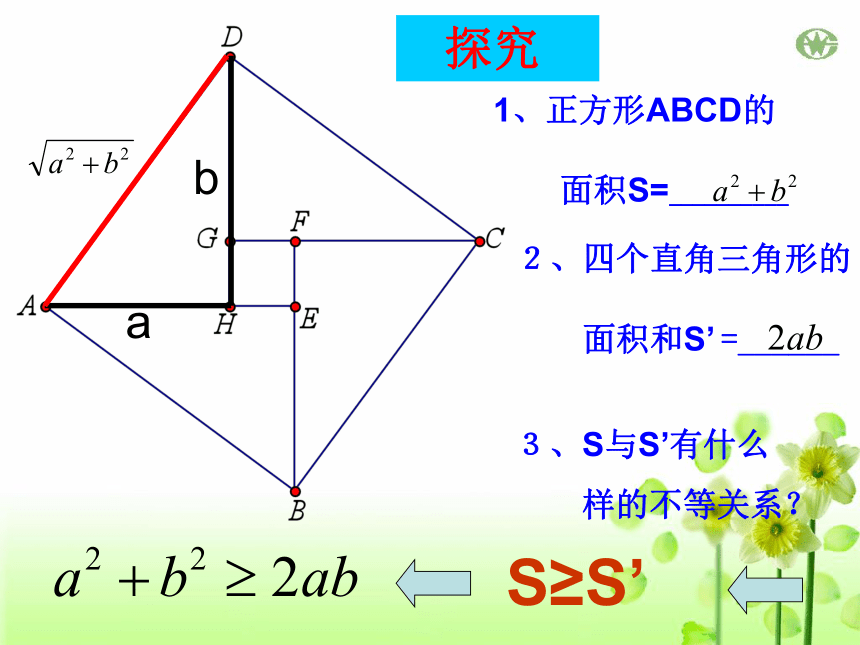
1、正方形ABCD的
面积S=__________
2、四个直角三角形的
面积和S’ =______
3、S与S’有什么
样的不等关系?
探究
S≥S’
a2+b2≥2ab
思考:
(1)该结论成立的条件是什么 ?
若a,b∈R,那么
(2)公式中等号成立的条件是什么?
(当且仅当a=b时,取“=”号)
若a,b∈R,那么a2+b2≥2ab (当且仅当a=b时,等号成立)
思考3 :不等式左右两边有何种运算结构?
任意两数的平方和不小于它们的积的两倍
由此公式,我们可以变形为
思考:以下不等式成立吗?
若a,b∈R,那么a2+b2≥2ab (当且仅当a=b时,等号成立)
若a>0 b>0
(当且仅当a=b时,等号成立)
那么a + b ≥2
基本不等式的证明
1 作差比较法;
2 换元法;
3 反证法;
4 几何解释法。
探究2:
A
B
C
D
E
1、如图,AB是圆的直径,C是AB上与A、B不重合的一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连AD,BD,
则CD=__,半径=____
a
b
半弦不大于半径
2、你能用这个图形得出基本不等式
几何解释吗
O
基本不等式
当且仅当a=b时,等号成立。
算术平均数
几何平均数
1.两个正数的算术平均数不小于它们的几何平均数.
2.两个正数的等差中项不小于它们的等比中项
3.变形用
例题1
例2.(1) 已知 并指出等号
成立的条件.
(2) 已知 与2的大小关系,
并说明理由.
(3) 已知 能得到什么结论
请说明理由.
练习
1、已知a、b、c都是正数,求证:
(a+b)(b+c)(c+a)≥8abc
1 今天这节课学了哪些主要知识?
(1)重要不等式和基本不等式各自成立的条件及结构特征 (2)基本不等式的简单应用
2 在解决问题时用了哪些方法? (1)数形结合思想 (2)换元法、作差比较法
(3)类比、配凑等技巧
你会了吗?
思考:我们已经知道
那么,在 的条件下,你能比较
的大小吗?
由此,你可以得到什么结论呢?
必做题:(1)课本第100页练习1;
(2)习题3.4 A组第1题.
选作题:几何解释法是一种很好的证明不等式的方法,你能否再尝试一下利用其他几何图形来证明这两个不等式吗?
3.4 基本不等式:
华南师大附中 曲政
ICM2002会标
如图,这是在北京召开的第22届国际数学家大会会标.会标根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车,代表中国人民热情好客。
a
b
1、正方形ABCD的
面积S=__________
2、四个直角三角形的
面积和S’ =______
3、S与S’有什么
样的不等关系?
探究
S≥S’
a2+b2≥2ab
思考:
(1)该结论成立的条件是什么 ?
若a,b∈R,那么
(2)公式中等号成立的条件是什么?
(当且仅当a=b时,取“=”号)
若a,b∈R,那么a2+b2≥2ab (当且仅当a=b时,等号成立)
思考3 :不等式左右两边有何种运算结构?
任意两数的平方和不小于它们的积的两倍
由此公式,我们可以变形为
思考:以下不等式成立吗?
若a,b∈R,那么a2+b2≥2ab (当且仅当a=b时,等号成立)
若a>0 b>0
(当且仅当a=b时,等号成立)
那么a + b ≥2
基本不等式的证明
1 作差比较法;
2 换元法;
3 反证法;
4 几何解释法。
探究2:
A
B
C
D
E
1、如图,AB是圆的直径,C是AB上与A、B不重合的一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连AD,BD,
则CD=__,半径=____
a
b
半弦不大于半径
2、你能用这个图形得出基本不等式
几何解释吗
O
基本不等式
当且仅当a=b时,等号成立。
算术平均数
几何平均数
1.两个正数的算术平均数不小于它们的几何平均数.
2.两个正数的等差中项不小于它们的等比中项
3.变形用
例题1
例2.(1) 已知 并指出等号
成立的条件.
(2) 已知 与2的大小关系,
并说明理由.
(3) 已知 能得到什么结论
请说明理由.
练习
1、已知a、b、c都是正数,求证:
(a+b)(b+c)(c+a)≥8abc
1 今天这节课学了哪些主要知识?
(1)重要不等式和基本不等式各自成立的条件及结构特征 (2)基本不等式的简单应用
2 在解决问题时用了哪些方法? (1)数形结合思想 (2)换元法、作差比较法
(3)类比、配凑等技巧
你会了吗?
思考:我们已经知道
那么,在 的条件下,你能比较
的大小吗?
由此,你可以得到什么结论呢?
必做题:(1)课本第100页练习1;
(2)习题3.4 A组第1题.
选作题:几何解释法是一种很好的证明不等式的方法,你能否再尝试一下利用其他几何图形来证明这两个不等式吗?
