2021-2022学年度人教版九年级数学上册第二十五章 概率初步单元卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年度人教版九年级数学上册第二十五章 概率初步单元卷(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 157.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 11:02:02 | ||
图片预览




文档简介
2021-2022学年度人教版九年级数学上册第二十五章 概率初步单元卷
一、选择题
1.下列事件中,是随机事件的是(?? ).
A.?从背面朝上的5张红桃和5张梅花扑克牌中抽取一张牌,恰好是方块
B.?抛掷一枚普通硬币9次是正面,抛掷第10次恰好是正面
C.?从装有10个黑球的不透明箱子中随机摸出1个球,恰好是黑球
D.?抛掷一枚质地均匀的正方体骰子,出现的点数不是奇数就是偶数
2.三年一班班长的钥匙串上有5把钥匙,其中两把是开本班教室门锁的随意用一把钥匙开本班教室门,能打开本班教室门锁的概率为(? )
A.?23?????????????????????????????B.?25????????????????????????C.?13?????????????????D.?16
3.现有4条线段,长度依次是2、5、7、8,从中任选三条,能组成三角形的概率是(??? )
A.?12?????????????????????????B.?214???????????????????????C.?35?????????????????????????D.?34
4.为了估计某地区梅花鹿的数量,先捕捉20只梅花鹿做上标记,然后放走,待有标记的梅花鹿完全混合于鹿群后,第二次捕捉100只梅花鹿,发现其中5只有标记.估计这个地区的梅花鹿的数量约有(??? )只.
A.?200???????????????B.?300?????????????????C.?400?????????????????????D.?500
5.育种小组对某品种小麦发芽情况进行测试,在测试基本情况相同的条件下,得到如下数据:
抽查小麦粒数
100
500
1000
2000
3000
4000
发芽粒数
95
486
968
1940
2907
a
则a的值最有可能是(??? )
A.?3680?????????????????B.?3720???????????C.?3880??????????????????????D.?3960
6.某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等。某天甲、乙两位乘客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是(?? )
A.?15???????????????????B.?14????????????????????????C.?13???????????????????????D.?12
7.有一首《对子歌》中唱到:天对地,雨对风,大陆对长空.现将“天,雨,大,空”四个字书写在材质、大小完全相同的卡片上,在暗箱搅匀后,随机抽取两张,恰为“天”、“空”二字的概率为(?? )
A.?13??????????????????????B.?14????????????????????????????????C.?15??????????????????????????????????????D.?16
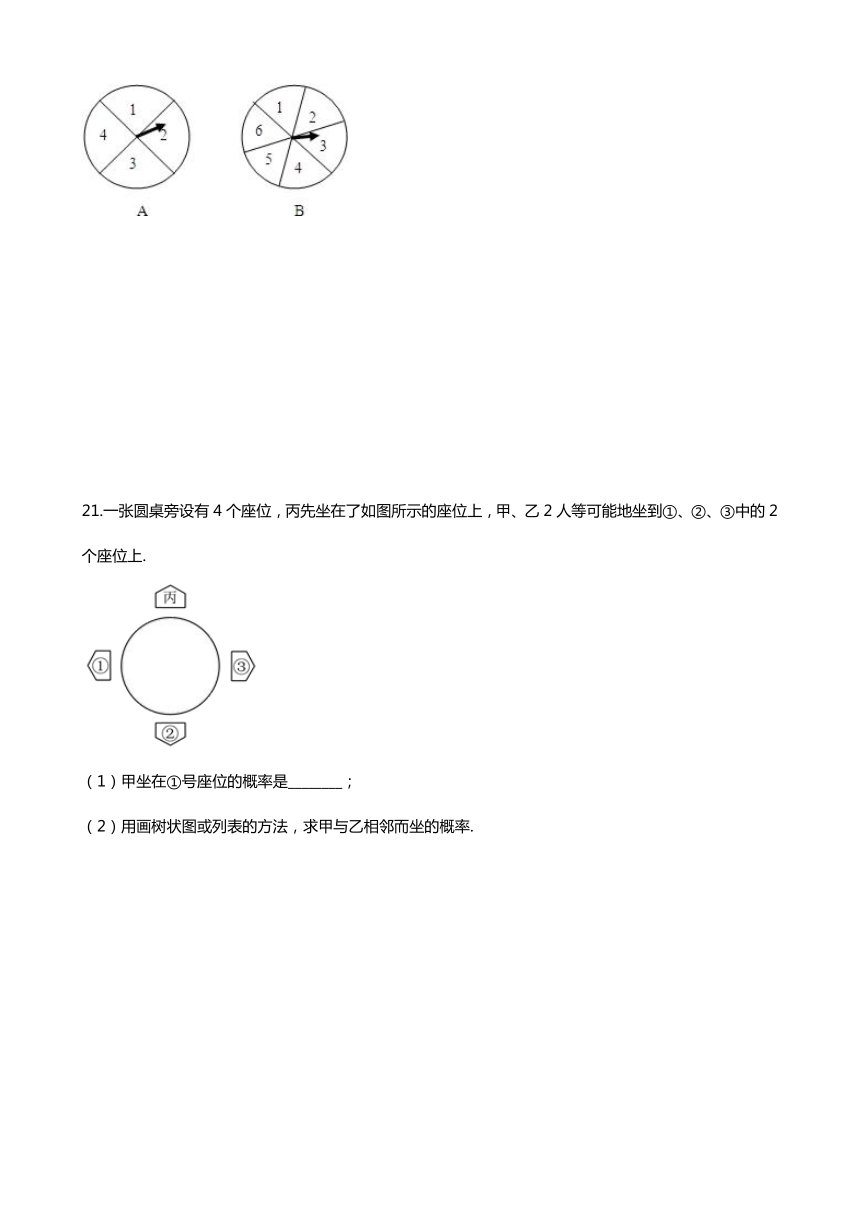
8.如图所示的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在奇数上的概率是(??? )
A.?15??????????????????????????????B.?310???????????????????????????????C.?25????????????????????????????D.?12
9.疫情期间进入学校都要进入测温通道,体温正常才可进入学校,昌平某校有2个测温通道,分别记为A、B通道,学生可随机选取其中的一个通道测温进校园.某日早晨该校所有学生体温正常.小王和小李两同学该日早晨进校园时,选择同一通道测温进校园的概率是(?? )
A.?14??????????????????????????????B.?13?????????????????????????C.?12???????????????????D.?23
10.甲袋中装有2张相同的卡片,颜色分别为红色和黄色;乙袋中装有3张相同的卡片,颜色分别为红色、黄色、绿色.从这两个口袋中各随机抽取1张卡片,取出的两张卡片中至少有一张是红色的概率是( )
A.?23??????????????????????????????????????????B.?12??????????????????????????????????????????C.?13??????????????????????????????????????????D.?16
二、填空题
11.一个不透明的袋中装有21个只有颜色不同的球,其中5个红球,7个白球,9个黄球.从中任意摸出1个球是红球的概率为________.
12.不透明袋子中装有黑球1个、白球2个,这些球除了颜色外无其他差别.从袋子中随机摸出一个球,记下颜色后放回,将袋子中的球摇匀,再随机摸出一个球,记下颜色,前后两次摸出的球都是白球的概率是________.
13.在﹣2,0,1,2这四个数中任取两数m,n,则二次函数y=(x﹣m)2+n的顶点在坐标轴上的概率为________.
14.一个不透明的口袋中装有2个红球和若干个白球,它们除颜色外其它完全相同.通过多次摸球实验后发现,摸到红球的频率稳定在20%附近,口袋中白球最有可能有________个;
15.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.随机摸取一个小球不放回,再从口袋中随机摸出一个小球,两次取出的小球标号的和不大于4的概率是________.
16.在同样条件下,对某种小麦种子进行发芽试验,统计如下表:
试验种子粒数
50
100
200
500
1000
2000
3000
发芽种子粒数
45
92
188
476
951
1900
2850
据此估计该小麦种子发芽的概率为________(精确到0.01).
三、解答题
17.篮球课上,朱老师向学生详细地讲解传球的要领时,叫甲、乙、丙、丁四位同学配合朱老师进行传球训练,朱老师把球传给甲同学后,让四位同学相互传球,其他人观看体会,当甲同学第一个传球时,求甲同学传给下一个同学后,这个同学再传给甲同学的概率
18.有四张正面分别写有数字:20,15,10,5的卡片,背面完全相同,将卡片洗匀后背面朝上.放在桌面上小明先随机抽取一张,记下牌面上的数字(不放回),再从剩下的卡片中随机抽取一张,记下牌面上的数字.如果卡片上的数字分别对应价值为20元,15元,10元,5元的四件奖品,请用列表或画树状图法求小明两次所获奖品总值不低于30元的概率?
19.小华有三张卡片,小明有两张卡片,卡片除正面上的数字不同外其它都相同,卡片上的数字如图所示.小华从自己的三张卡片中随机抽取一张,之后小明也从自己的两张卡片中随机抽取一张,请用画树状图(或列表)的方法,求抽取的两张卡片上的数字和为7的概率.
20.如图,有两个可以自由转动的转盘A、B,转盘A被均匀分成4等份,每份标上数字1、2、3、4四个数字;转盘B被均匀分成6等份,每份标上数字1、2、3、4、5、6六个数字.有人为甲乙两人设计了一个游戏,其规则如下:
同时转动转盘A与B,转盘停止后,指针各指向一个数字(如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止),用所指的两个数字作乘积,如果所得的积是偶数,那么甲得1分;如果所得的积是奇数,那么乙得1分.你认为这样的规则是否公平?请你说明理由;如果不公平,请你修改规则使该游戏对双方公平.
21.一张圆桌旁设有4个座位,丙先坐在了如图所示的座位上,甲、乙2人等可能地坐到①、②、③中的2个座位上.
(1)甲坐在①号座位的概率是________;
(2)用画树状图或列表的方法,求甲与乙相邻而坐的概率.
22.一个不透明的箱子里装有3个红色小球和若干个白色小球,每个小球除颜色外其他完全相同,每次把箱子里的小球摇匀后随机摸出一个小球,记下颜色后再放回箱子里,通过大量重复实验后,发现摸到红色小球的频率稳定于0.75左右.
(1)请你估计箱子里白色小球的个数;
(2)现从该箱子里摸出1个小球,记下颜色后放回箱子里,摇匀后,再摸出1个小球,求两次摸出的小球颜色恰好不同的概率(用画树状图或列表的方法).
23.为了参加全市中学生“党史知识竞赛”,某校准备从甲、乙2名女生和丙、丁2名男生中任选2人代表学校参加比赛.
(1)如果已经确定女生甲参加,再从其余的候选人中随机选取1人,则女生乙被选中的概率是________;
(2)求所选代表恰好为1名女生和1名男生的概率.
24.某茶农要对1号、2号、3号、4号四个品种共500株茶树幼苗进行移栽成活实验,从中选出成活率高的品种进行推广,通过实验得知,3号茶树幼苗成活率为89.6%,把实验数据绘制成图1和图2所示的两幅不完整的统计图.
(1)实验所用的2号茶树幼苗的数量是多少株?
(2)求出3号茶树幼苗的成活数,并补全统计图2;
(3)该茶农要从这四种茶树中选择两个品种进行推广,请用列表或画树状图的方法求出幼苗成活率最高的品种被选中的概率.
答案
一、选择题
1.解:A,从背面朝上的5张红桃和5张梅花扑克牌中抽取一张牌,恰好是方块,是不可能事件,故此项不符合题意;
B,抛掷一枚普通硬币9次是正面,抛掷第10次恰好是正面,是随机事件,故此项满足题意,
C,从装有10个黑球的不透明箱子中随机摸出1个球,恰好是黑球,是必然事件,故此项不满足题意;
D,抛掷一枚质地均匀的正方体骰子,出现的点数不是奇数就是偶数,是必然事件,故不满足题意;
故答案为:B
2.解:∵有2把钥匙能开教室门锁,共有5把钥匙,
∴小芳能打开教室门锁的可能性为: 25 .
故答案为:B.
3.解:现有4条线段,长度依次是2、5、7、8,从中任选三条,
共有以下4种情况:2、5、7;2、5、8;2、7、8;5、7、8;
其中能组成三角形有: 2、7、8;5、7、8;
所以能组成三角形的概率是 24=12 ;
故答案为:A.
4.解:设这个地区的梅花鹿的数量约有x只,
根据题意,得: 20x=5100 ,
解得 x=400 ,
经检验: x=400 是分式方程的解,
所以这个地区的梅花鹿的数量约400只.
故答案为:C.
5.解:95÷100=0.95,
486÷500=0.972,
968÷1000=0.968,
1940÷2000=0.97,
2907÷3000=0.969,
由抽取的样本数据,我们发现小麦发芽的频率稳定在0.97左右,即用频率估计概率,我们可估计小麦发芽的概率为0.97,
所以,a=4000×0.97=3880,
所以,a最有可能为3880,
故答案为:C.
6.解:将3节车厢分别记为1号车厢,2号车厢,3号车厢,用树状图表示所有等可能的结果,
共有9种等可能的结果,其中,甲和乙从同一节车厢上车的有3可能,
即甲和乙从同一节车厢上车的概率是 39=13 ,
故答案为:C.
7.解:画树状图如下:
由树状图知,共有12种等可能结果,其中恰为“天”、“空”的有2种结果,
∴ 恰为“天”、“空”的概率为 212=16 ,
故答案为:D.
8.解:列表得:
?
1
2
3
4
5
3
(1,3)
(2,3)
(3,3)
(4,3)
(5,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
(5,4)
8
(1,8)
(2,8)
(3,8)
(4,8)
(5,8)
9
(1,9)
(2,9)
(3,9)
(4,9)
(5,9)
所以两个转盘的组合有20种结果,其中有6种指针都落在奇数,
所以指针都落在奇数上的概率是6÷20= 310 ,
故答案为:B.
9.解:列表格如下:
?
A
B
A
A , A
B , A
B
A , B
B , B
由表可知,共有4种等可能的结果,其中小王和小李从同一个测温通道通过的有2种可能,
所以小王和小李从同一个测温通道通过的概率为 24=12 .
故答案为:C
10.解:画树状图如图:
共有6个等可能的结果,取出的两张卡片中至少有一张是红色的结果有4个,
∴ 取出的两张卡片中至少有一张是红色的概率为 46=23 ,
故答案为:A.
二、填空题
11.解:∵袋子中共有21个小球,其中红球有5个,
∴摸出一个球是红球的概率是 521 ,
故答案为: 521 .
12.解:列表如图所示:
?
黑
白
白
黑
(黑,黑)
(白,黑)
(白,黑)
白
(黑,白)
(白,白)
(白,白)
白
(黑,白)
(白,白)
(白,白)
由上表可知,所有等可能的情况共有9种,
其中两次摸出的球都是白球的情况共有4种,
∴两次摸出的球都是白球的概率 P=49 ,
故答案为: 49 .
13.解:画树状图为:
共有12种等可能的结果数,其中二次函数y=(x﹣m)2+n的顶点在坐标轴上的结果数为6,
所以二次函数y=(x﹣m)2+n的顶点在坐标轴上的概率= 612 = 12 ,
故答案为: 12 .
14.解:设白球个数为:x个,
∵摸到红色球的频率稳定在20%左右,
∴口袋中得到红色球的概率为20%,
∴ 22+x = 15 ,
解得:x=8,
故白球的个数为8个.
故答案为8.
15.解:画树状图如下:
共有12种等可能的结果,两次取出的小球标号的和不大于4的结果有4种,
∴两次取出的小球标号的和不大于4的概率为: 412=13 ,
故答案为: 13 .
16.解:∵在同样条件下,对某种小麦种子粒数3000粒时,种子发芽的频数为2850粒,
∴种子发芽的频率为P= =28503000=0.95 ,
∵在大数次的实验情况下,频率趋于一个稳定值,即概率,
∴估计小麦种子发芽的概率为0.95.
故答案为0.95.
三、解答题
17. 解:由题意可画如下的树状图:
∵ 由树状图可知,共有9种等可能性的结果,其中甲同学传给下一个同学后,这个同学再传给甲同学的结果有3种
∴ 甲同学传给下一个同学后,这个同学再传给甲同学的概率 39=13 .
18. 解:列表如下:
20
15
10
5
20
35
30
25
15
35
25
20
10
30
25
15
5
25
20
15
由表格知,共有12种等可能结果,其中两次所获奖品总值不低于30元的有4种结果,
∴小明两次所获奖品总值不低于30元的概率为 412=13.
19. 解:画树状图如图:
共有6种等可能的结果,抽取的两张卡片上的数字和为7的结果有3种,
∴ 抽取的两张卡片上的数字和为7的概率为 36=12 .
20. 解:列表如下,
1
2
3
4
5
6
1
奇
偶
奇
偶
奇
偶
2
偶
偶
偶
偶
偶
偶
3
奇
偶
奇
偶
奇
偶
4
偶
偶
偶
偶
偶
偶
?从表中可以看出所得的积共有4×6=24种情况,
乘积是奇数的结果共有2×3=6种情况,
所以甲获胜的概率是 34 ,乙获胜的概率是 14 .
所以这个游戏规则不公平.
游戏规则可以改为:当两数的和是奇数时甲获胜,当两数和是偶数时乙获胜.
21.(1)13
(2)解:画树状图如图:
共有6种等可能的结果,甲与乙两同学恰好相邻而坐的结果有4种,
∴甲与乙相邻而坐的概率为 46 = 23
解:(1)∵丙坐了一张座位,
∴甲坐在①号座位的概率是 13 ;
22. (1)解:∵通过多次摸球试验后发现,摸到红球的频率稳定在0.75左右,
∴估计摸到红球的概率为0.75,
设白球有 x 个,依题意得 33+x=0.75
解得, x=1 .
经检验: x=1 是原方程的解,且符合题意,
所以箱子里可能有1个白球
(2)解:列表如下:
红 1
红 2
红 3
白
红 1
(红 1 ,红 1 )
(红 1 ,红 2 )
(红 1 ,红)
(红 1 ,白)
红 2
(红 2 ,红 1 )
(红 2 ,红 2 )
(红 2 ,红)
(红 2 ,白)
红 3
(红 3 ,红 1 )
(红 3 ,红 2 )
(红 3 ,红 3 )
(红 3 ,白)
白
(白,红 1 )
(白,红 2 )
(白,红)
(白,白)
或画树状图如下:
∵一共有16种等可能的结果,两次摸出的小球颜色恰好不同的有:
(红 1 ,白)、(红 2 ,白)、(红 3 ,白)、(白,红 1 )、(白,红 2 )、(白,红 3 )共6种.
∴两次摸出的小球恰好颜色不同的概率 616=38
23. (1)13
(2)解:分别用字母A,B表示女生,C,D表示男生
画树状如下:
4人任选2人共有12种等可能结果,其中1名女生和1名男生有8种,
∴ P (1女1男) =812=23 .
答:所选代表恰好为1名女生和1名男生的概率是 23
解:(1)∵已确定女生甲参加比赛,再从其余3名同学中随机选取1名有3种结果,其中恰好选中女生乙的只有1种,
∴恰好选中乙的概率为 13 ;
故答案为: 13 ;
24. (1)解: 500×(100%-30%-25%-25%)=100 株.
故实验所用的2号茶树幼苗的数量是100株.
(2)解: 500×25%×89.6%=112 株.
故3号茶树幼苗的成活数是112株, 补全条形图如下:
(3)解:1号茶树幼苗的成活率为 115500×30%×100%=90% ;
2号茶树幼苗的成活率为 85100×100%=85% ;
3号茶树幼苗的成活率为 89.6% ;
4号茶树幼苗的成活率为 117500×25%×100%=93.6% .
故4号茶树幼苗的成活率最高.
画树状图如下:
由树状图知共有12种等可能结果,其中抽到4号茶树幼苗的有6种结果,
所以4号品种被选中的概率为 612=12 .
故幼苗成活率最高的品种被选中的概率为 12 .
一、选择题
1.下列事件中,是随机事件的是(?? ).
A.?从背面朝上的5张红桃和5张梅花扑克牌中抽取一张牌,恰好是方块
B.?抛掷一枚普通硬币9次是正面,抛掷第10次恰好是正面
C.?从装有10个黑球的不透明箱子中随机摸出1个球,恰好是黑球
D.?抛掷一枚质地均匀的正方体骰子,出现的点数不是奇数就是偶数
2.三年一班班长的钥匙串上有5把钥匙,其中两把是开本班教室门锁的随意用一把钥匙开本班教室门,能打开本班教室门锁的概率为(? )
A.?23?????????????????????????????B.?25????????????????????????C.?13?????????????????D.?16
3.现有4条线段,长度依次是2、5、7、8,从中任选三条,能组成三角形的概率是(??? )
A.?12?????????????????????????B.?214???????????????????????C.?35?????????????????????????D.?34
4.为了估计某地区梅花鹿的数量,先捕捉20只梅花鹿做上标记,然后放走,待有标记的梅花鹿完全混合于鹿群后,第二次捕捉100只梅花鹿,发现其中5只有标记.估计这个地区的梅花鹿的数量约有(??? )只.
A.?200???????????????B.?300?????????????????C.?400?????????????????????D.?500
5.育种小组对某品种小麦发芽情况进行测试,在测试基本情况相同的条件下,得到如下数据:
抽查小麦粒数
100
500
1000
2000
3000
4000
发芽粒数
95
486
968
1940
2907
a
则a的值最有可能是(??? )
A.?3680?????????????????B.?3720???????????C.?3880??????????????????????D.?3960
6.某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等。某天甲、乙两位乘客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是(?? )
A.?15???????????????????B.?14????????????????????????C.?13???????????????????????D.?12
7.有一首《对子歌》中唱到:天对地,雨对风,大陆对长空.现将“天,雨,大,空”四个字书写在材质、大小完全相同的卡片上,在暗箱搅匀后,随机抽取两张,恰为“天”、“空”二字的概率为(?? )
A.?13??????????????????????B.?14????????????????????????????????C.?15??????????????????????????????????????D.?16
8.如图所示的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在奇数上的概率是(??? )
A.?15??????????????????????????????B.?310???????????????????????????????C.?25????????????????????????????D.?12
9.疫情期间进入学校都要进入测温通道,体温正常才可进入学校,昌平某校有2个测温通道,分别记为A、B通道,学生可随机选取其中的一个通道测温进校园.某日早晨该校所有学生体温正常.小王和小李两同学该日早晨进校园时,选择同一通道测温进校园的概率是(?? )
A.?14??????????????????????????????B.?13?????????????????????????C.?12???????????????????D.?23
10.甲袋中装有2张相同的卡片,颜色分别为红色和黄色;乙袋中装有3张相同的卡片,颜色分别为红色、黄色、绿色.从这两个口袋中各随机抽取1张卡片,取出的两张卡片中至少有一张是红色的概率是( )
A.?23??????????????????????????????????????????B.?12??????????????????????????????????????????C.?13??????????????????????????????????????????D.?16
二、填空题
11.一个不透明的袋中装有21个只有颜色不同的球,其中5个红球,7个白球,9个黄球.从中任意摸出1个球是红球的概率为________.
12.不透明袋子中装有黑球1个、白球2个,这些球除了颜色外无其他差别.从袋子中随机摸出一个球,记下颜色后放回,将袋子中的球摇匀,再随机摸出一个球,记下颜色,前后两次摸出的球都是白球的概率是________.
13.在﹣2,0,1,2这四个数中任取两数m,n,则二次函数y=(x﹣m)2+n的顶点在坐标轴上的概率为________.
14.一个不透明的口袋中装有2个红球和若干个白球,它们除颜色外其它完全相同.通过多次摸球实验后发现,摸到红球的频率稳定在20%附近,口袋中白球最有可能有________个;
15.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.随机摸取一个小球不放回,再从口袋中随机摸出一个小球,两次取出的小球标号的和不大于4的概率是________.
16.在同样条件下,对某种小麦种子进行发芽试验,统计如下表:
试验种子粒数
50
100
200
500
1000
2000
3000
发芽种子粒数
45
92
188
476
951
1900
2850
据此估计该小麦种子发芽的概率为________(精确到0.01).
三、解答题
17.篮球课上,朱老师向学生详细地讲解传球的要领时,叫甲、乙、丙、丁四位同学配合朱老师进行传球训练,朱老师把球传给甲同学后,让四位同学相互传球,其他人观看体会,当甲同学第一个传球时,求甲同学传给下一个同学后,这个同学再传给甲同学的概率
18.有四张正面分别写有数字:20,15,10,5的卡片,背面完全相同,将卡片洗匀后背面朝上.放在桌面上小明先随机抽取一张,记下牌面上的数字(不放回),再从剩下的卡片中随机抽取一张,记下牌面上的数字.如果卡片上的数字分别对应价值为20元,15元,10元,5元的四件奖品,请用列表或画树状图法求小明两次所获奖品总值不低于30元的概率?
19.小华有三张卡片,小明有两张卡片,卡片除正面上的数字不同外其它都相同,卡片上的数字如图所示.小华从自己的三张卡片中随机抽取一张,之后小明也从自己的两张卡片中随机抽取一张,请用画树状图(或列表)的方法,求抽取的两张卡片上的数字和为7的概率.
20.如图,有两个可以自由转动的转盘A、B,转盘A被均匀分成4等份,每份标上数字1、2、3、4四个数字;转盘B被均匀分成6等份,每份标上数字1、2、3、4、5、6六个数字.有人为甲乙两人设计了一个游戏,其规则如下:
同时转动转盘A与B,转盘停止后,指针各指向一个数字(如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止),用所指的两个数字作乘积,如果所得的积是偶数,那么甲得1分;如果所得的积是奇数,那么乙得1分.你认为这样的规则是否公平?请你说明理由;如果不公平,请你修改规则使该游戏对双方公平.
21.一张圆桌旁设有4个座位,丙先坐在了如图所示的座位上,甲、乙2人等可能地坐到①、②、③中的2个座位上.
(1)甲坐在①号座位的概率是________;
(2)用画树状图或列表的方法,求甲与乙相邻而坐的概率.
22.一个不透明的箱子里装有3个红色小球和若干个白色小球,每个小球除颜色外其他完全相同,每次把箱子里的小球摇匀后随机摸出一个小球,记下颜色后再放回箱子里,通过大量重复实验后,发现摸到红色小球的频率稳定于0.75左右.
(1)请你估计箱子里白色小球的个数;
(2)现从该箱子里摸出1个小球,记下颜色后放回箱子里,摇匀后,再摸出1个小球,求两次摸出的小球颜色恰好不同的概率(用画树状图或列表的方法).
23.为了参加全市中学生“党史知识竞赛”,某校准备从甲、乙2名女生和丙、丁2名男生中任选2人代表学校参加比赛.
(1)如果已经确定女生甲参加,再从其余的候选人中随机选取1人,则女生乙被选中的概率是________;
(2)求所选代表恰好为1名女生和1名男生的概率.
24.某茶农要对1号、2号、3号、4号四个品种共500株茶树幼苗进行移栽成活实验,从中选出成活率高的品种进行推广,通过实验得知,3号茶树幼苗成活率为89.6%,把实验数据绘制成图1和图2所示的两幅不完整的统计图.
(1)实验所用的2号茶树幼苗的数量是多少株?
(2)求出3号茶树幼苗的成活数,并补全统计图2;
(3)该茶农要从这四种茶树中选择两个品种进行推广,请用列表或画树状图的方法求出幼苗成活率最高的品种被选中的概率.
答案
一、选择题
1.解:A,从背面朝上的5张红桃和5张梅花扑克牌中抽取一张牌,恰好是方块,是不可能事件,故此项不符合题意;
B,抛掷一枚普通硬币9次是正面,抛掷第10次恰好是正面,是随机事件,故此项满足题意,
C,从装有10个黑球的不透明箱子中随机摸出1个球,恰好是黑球,是必然事件,故此项不满足题意;
D,抛掷一枚质地均匀的正方体骰子,出现的点数不是奇数就是偶数,是必然事件,故不满足题意;
故答案为:B
2.解:∵有2把钥匙能开教室门锁,共有5把钥匙,
∴小芳能打开教室门锁的可能性为: 25 .
故答案为:B.
3.解:现有4条线段,长度依次是2、5、7、8,从中任选三条,
共有以下4种情况:2、5、7;2、5、8;2、7、8;5、7、8;
其中能组成三角形有: 2、7、8;5、7、8;
所以能组成三角形的概率是 24=12 ;
故答案为:A.
4.解:设这个地区的梅花鹿的数量约有x只,
根据题意,得: 20x=5100 ,
解得 x=400 ,
经检验: x=400 是分式方程的解,
所以这个地区的梅花鹿的数量约400只.
故答案为:C.
5.解:95÷100=0.95,
486÷500=0.972,
968÷1000=0.968,
1940÷2000=0.97,
2907÷3000=0.969,
由抽取的样本数据,我们发现小麦发芽的频率稳定在0.97左右,即用频率估计概率,我们可估计小麦发芽的概率为0.97,
所以,a=4000×0.97=3880,
所以,a最有可能为3880,
故答案为:C.
6.解:将3节车厢分别记为1号车厢,2号车厢,3号车厢,用树状图表示所有等可能的结果,
共有9种等可能的结果,其中,甲和乙从同一节车厢上车的有3可能,
即甲和乙从同一节车厢上车的概率是 39=13 ,
故答案为:C.
7.解:画树状图如下:
由树状图知,共有12种等可能结果,其中恰为“天”、“空”的有2种结果,
∴ 恰为“天”、“空”的概率为 212=16 ,
故答案为:D.
8.解:列表得:
?
1
2
3
4
5
3
(1,3)
(2,3)
(3,3)
(4,3)
(5,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
(5,4)
8
(1,8)
(2,8)
(3,8)
(4,8)
(5,8)
9
(1,9)
(2,9)
(3,9)
(4,9)
(5,9)
所以两个转盘的组合有20种结果,其中有6种指针都落在奇数,
所以指针都落在奇数上的概率是6÷20= 310 ,
故答案为:B.
9.解:列表格如下:
?
A
B
A
A , A
B , A
B
A , B
B , B
由表可知,共有4种等可能的结果,其中小王和小李从同一个测温通道通过的有2种可能,
所以小王和小李从同一个测温通道通过的概率为 24=12 .
故答案为:C
10.解:画树状图如图:
共有6个等可能的结果,取出的两张卡片中至少有一张是红色的结果有4个,
∴ 取出的两张卡片中至少有一张是红色的概率为 46=23 ,
故答案为:A.
二、填空题
11.解:∵袋子中共有21个小球,其中红球有5个,
∴摸出一个球是红球的概率是 521 ,
故答案为: 521 .
12.解:列表如图所示:
?
黑
白
白
黑
(黑,黑)
(白,黑)
(白,黑)
白
(黑,白)
(白,白)
(白,白)
白
(黑,白)
(白,白)
(白,白)
由上表可知,所有等可能的情况共有9种,
其中两次摸出的球都是白球的情况共有4种,
∴两次摸出的球都是白球的概率 P=49 ,
故答案为: 49 .
13.解:画树状图为:
共有12种等可能的结果数,其中二次函数y=(x﹣m)2+n的顶点在坐标轴上的结果数为6,
所以二次函数y=(x﹣m)2+n的顶点在坐标轴上的概率= 612 = 12 ,
故答案为: 12 .
14.解:设白球个数为:x个,
∵摸到红色球的频率稳定在20%左右,
∴口袋中得到红色球的概率为20%,
∴ 22+x = 15 ,
解得:x=8,
故白球的个数为8个.
故答案为8.
15.解:画树状图如下:
共有12种等可能的结果,两次取出的小球标号的和不大于4的结果有4种,
∴两次取出的小球标号的和不大于4的概率为: 412=13 ,
故答案为: 13 .
16.解:∵在同样条件下,对某种小麦种子粒数3000粒时,种子发芽的频数为2850粒,
∴种子发芽的频率为P= =28503000=0.95 ,
∵在大数次的实验情况下,频率趋于一个稳定值,即概率,
∴估计小麦种子发芽的概率为0.95.
故答案为0.95.
三、解答题
17. 解:由题意可画如下的树状图:
∵ 由树状图可知,共有9种等可能性的结果,其中甲同学传给下一个同学后,这个同学再传给甲同学的结果有3种
∴ 甲同学传给下一个同学后,这个同学再传给甲同学的概率 39=13 .
18. 解:列表如下:
20
15
10
5
20
35
30
25
15
35
25
20
10
30
25
15
5
25
20
15
由表格知,共有12种等可能结果,其中两次所获奖品总值不低于30元的有4种结果,
∴小明两次所获奖品总值不低于30元的概率为 412=13.
19. 解:画树状图如图:
共有6种等可能的结果,抽取的两张卡片上的数字和为7的结果有3种,
∴ 抽取的两张卡片上的数字和为7的概率为 36=12 .
20. 解:列表如下,
1
2
3
4
5
6
1
奇
偶
奇
偶
奇
偶
2
偶
偶
偶
偶
偶
偶
3
奇
偶
奇
偶
奇
偶
4
偶
偶
偶
偶
偶
偶
?从表中可以看出所得的积共有4×6=24种情况,
乘积是奇数的结果共有2×3=6种情况,
所以甲获胜的概率是 34 ,乙获胜的概率是 14 .
所以这个游戏规则不公平.
游戏规则可以改为:当两数的和是奇数时甲获胜,当两数和是偶数时乙获胜.
21.(1)13
(2)解:画树状图如图:
共有6种等可能的结果,甲与乙两同学恰好相邻而坐的结果有4种,
∴甲与乙相邻而坐的概率为 46 = 23
解:(1)∵丙坐了一张座位,
∴甲坐在①号座位的概率是 13 ;
22. (1)解:∵通过多次摸球试验后发现,摸到红球的频率稳定在0.75左右,
∴估计摸到红球的概率为0.75,
设白球有 x 个,依题意得 33+x=0.75
解得, x=1 .
经检验: x=1 是原方程的解,且符合题意,
所以箱子里可能有1个白球
(2)解:列表如下:
红 1
红 2
红 3
白
红 1
(红 1 ,红 1 )
(红 1 ,红 2 )
(红 1 ,红)
(红 1 ,白)
红 2
(红 2 ,红 1 )
(红 2 ,红 2 )
(红 2 ,红)
(红 2 ,白)
红 3
(红 3 ,红 1 )
(红 3 ,红 2 )
(红 3 ,红 3 )
(红 3 ,白)
白
(白,红 1 )
(白,红 2 )
(白,红)
(白,白)
或画树状图如下:
∵一共有16种等可能的结果,两次摸出的小球颜色恰好不同的有:
(红 1 ,白)、(红 2 ,白)、(红 3 ,白)、(白,红 1 )、(白,红 2 )、(白,红 3 )共6种.
∴两次摸出的小球恰好颜色不同的概率 616=38
23. (1)13
(2)解:分别用字母A,B表示女生,C,D表示男生
画树状如下:
4人任选2人共有12种等可能结果,其中1名女生和1名男生有8种,
∴ P (1女1男) =812=23 .
答:所选代表恰好为1名女生和1名男生的概率是 23
解:(1)∵已确定女生甲参加比赛,再从其余3名同学中随机选取1名有3种结果,其中恰好选中女生乙的只有1种,
∴恰好选中乙的概率为 13 ;
故答案为: 13 ;
24. (1)解: 500×(100%-30%-25%-25%)=100 株.
故实验所用的2号茶树幼苗的数量是100株.
(2)解: 500×25%×89.6%=112 株.
故3号茶树幼苗的成活数是112株, 补全条形图如下:
(3)解:1号茶树幼苗的成活率为 115500×30%×100%=90% ;
2号茶树幼苗的成活率为 85100×100%=85% ;
3号茶树幼苗的成活率为 89.6% ;
4号茶树幼苗的成活率为 117500×25%×100%=93.6% .
故4号茶树幼苗的成活率最高.
画树状图如下:
由树状图知共有12种等可能结果,其中抽到4号茶树幼苗的有6种结果,
所以4号品种被选中的概率为 612=12 .
故幼苗成活率最高的品种被选中的概率为 12 .
同课章节目录
