2021—2022学年冀教版九年级数学上册第二十八章 圆 练习题(Word版含答案)
文档属性
| 名称 | 2021—2022学年冀教版九年级数学上册第二十八章 圆 练习题(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 490.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-02 09:47:16 | ||
图片预览




文档简介
第二十八章
圆
类型之一 确定圆的条件
1.下列说法中,正确的是( )
A.三点确定一个圆
B.三角形有且只有一个外接圆
C.四边形都有一个外接圆
D.以已知线段长为半径能确定一个圆
2.如图1,AC,BE是☉O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )
A.△ABE
B.△ACF
C.△ABD
D.△ADE
图1
图2
3.如图2,一圆弧过网格中的格点A,B,C,在网格中建立平面直角坐标系,使点A的坐标为(0,3),点C的坐标为(2,3),则该圆弧所在圆的圆心坐标是 .?
类型之二 弧、弦、圆心角与圆周角的关系
4.如图3,点A,B,C,D在☉O上,∠AOC=112°,B是的中点,则∠D的度数是( )
A.56°
B.35°
C.38°
D.28°
图3
图4
5.如图4,点A,B,S在圆上,若弦AB的长度等于圆半径的倍,则∠ASB的度数是( )
A.22.5°
B.30°
C.45°
D.60°
6.如图5,点A,B,C,D,E都是☉O上的点,,∠B=122°,则∠D的度数为( )
A.58°
B.116°
C.122°
D.128°
图5
图6
7.[2020·秦皇岛期末]
如图6,AB是☉O的直径,BC是弦,P是(含端点)上任意一点,若AB=13,BC=12,则AP的长不可能是( )
A.4
B.5
C.12
D.13
8.[2020·唐山丰润区期末]
如图7,AB为☉O的直径,点C,D在☉O上,若∠ABD=42°,则∠BCD的度数是 .?
图7
9.已知:如图8,△ABC内接于☉O,AF是☉O的弦,AF⊥BC,垂足为D,E为上一点,且BE=CF.
(1)求证:AE是☉O的直径;
(2)若∠ABC=∠CAE,AE=8,求AC的长.
图8
类型之三 利用垂径定理进行计算
10.[2020·唐山期末]
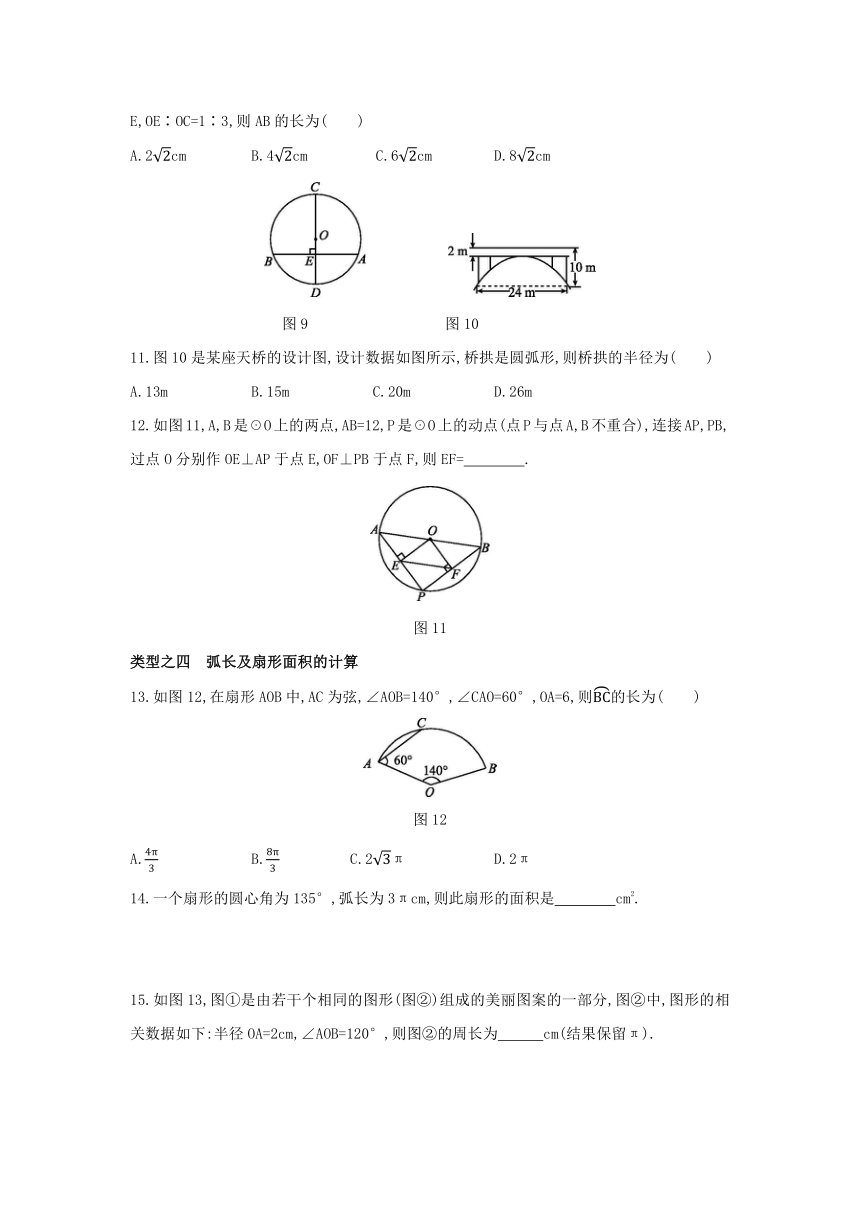
如图9,☉O的直径CD=12cm,AB是☉O的弦,AB⊥CD,垂足为E,OE∶OC=1∶3,则AB的长为( )
A.2cm
B.4cm
C.6cm
D.8cm
图9
图10
11.图10是某座天桥的设计图,设计数据如图所示,桥拱是圆弧形,则桥拱的半径为( )
A.13m
B.15m
C.20m
D.26m
12.如图11,A,B是☉O上的两点,AB=12,P是☉O上的动点(点P与点A,B不重合),连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF= .?
图11
类型之四 弧长及扇形面积的计算
13.如图12,在扇形AOB中,AC为弦,∠AOB=140°,∠CAO=60°,OA=6,则的长为( )
图12
A.
B.
C.2π
D.2π
14.一个扇形的圆心角为135°,弧长为3πcm,则此扇形的面积是 cm2.?
15.如图13,图①是由若干个相同的图形(图②)组成的美丽图案的一部分,图②中,图形的相关数据如下:半径OA=2cm,∠AOB=120°,则图②的周长为 cm(结果保留π).?
图13
图14
16.如图14,用一张半径为10cm的扇形纸板做一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的高为8cm,那么这张扇形纸板的弧长是 cm.?
17.[2020·唐山期末]
将两张半径均为10的半圆形的纸片完全重合叠放在一起,上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图15所示的图形,与直径AB交于点C,连接点C与圆心O'.
(1)求的长;
(2)求图中下面这张半圆形纸片未被上面这张纸片遮挡部分的面积S空白.
图15
类型之五 数学活动
18.一张圆形纸片,嘉琪进行了如下连续操作:
(1)将圆形纸片左右对折,折痕为AB,如图②所示.
(2)将圆形纸片上下折叠,使A,B两点重合,折痕CD与AB相交于点M,如图③所示.
(3)将圆形纸片沿EF折叠,使B,M两点重合,折痕EF与AB相交于点N,如图④所示.
(4)连接AE,AF,如图⑤所示.
经过以上操作嘉琪得到了以下结论:①CD∥EF;②四边形MEBF是菱形;③△AEF为等边三角形;④S△AEF∶S圆=3∶4π.以上结论正确的有( )
A.1个
B.2个
C.3个
D.4个
图16
【河北题型训练】
19.[2020·唐山期末]
如图17,把一个量角器放在∠BAC的上面,点B恰好在量角器上40°的位置,则∠BAC的度数是( )
A.40°
B.80°
C.20°
D.10°
图17
图18
20.[2020·石家庄模拟]
如图18,在6×6的正方形网格中,☉O经过格点A,B,C,点P是上任意一点,连接AP,BP,则tan∠APB的值为( )
A.
B.
C.
D.
21.[2020·河北]
有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆☉O,连接OB,OC.如图19,由∠BOC=2∠A=130°,得∠A=
65°.而淇淇说:“嘉嘉考虑得不周全,∠A还应有另一个不同的值.”下列判断正确的是( )
A.淇淇说得对,且∠A的另一个值是115°
B.淇淇说得不对,∠A就得65°
C.嘉嘉求的结果不对,∠A应得50°
D.两人都不对,∠A应有3个不同的值
图19
图20
22.[2020·石家庄模拟]
如图20,在平面直角坐标系中,A(6,0),B(0,2),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C的坐标为 ,扇形BAC的面积为 .?
23.[2020·河北节选]
如图21,O为AB的中点,分别延长OA到点C,OB到点D,使OC=OD.以点O为圆心,分别以OA,OC为半径在CD上方作两个半圆.点P为小半圆上任一点(不与点A,B重合),连接OP并延长交大半圆于点E,连接AE,CP.
(1)求证:△AOE≌△POC;
(2)写出∠1,∠2和∠C三者之间的数量关系,并说明理由.
图21
24.[2020·石家庄正定县期末]
如图22,在矩形ABCD中,AB=6,BC=8,点A在直线l上,AD与直线l相交所得的锐角为60°.点F在直线l上,AF=8,EF⊥直线l,垂足为F,且EF=6,以EF为直径,在EF的左侧作半圆O,M是半圆O上任一点.
发现:AM的最小值为 ,AM的最大值为 ,OB与直线l的位置关系是 .?
思考:矩形ABCD保持不动,半圆O沿直线l向左平移,当点E落在AD边上时,求半圆与矩形重合部分的周长和面积.
图22
答案
1.B
2.B [解析]各选项中,只有△ACF的三个顶点不都在圆上,故外心不是点O的是△ACF.
3.(1,0) [解析]如图,分别作弦AB,AC的垂直平分线,交于点D(1,0),所以该圆弧所在圆的圆心坐标是(1,0).
4.D [解析]如图,连接OB.∵B是的中点,∴∠AOB=∠AOC=56°.由圆周角定理,得∠D=∠AOB=28°.
5.C [解析]如图,设圆心为O,连接OA,OB.∵弦AB的长度等于圆半径的倍,即AB=OA.∵OA=OB,
∴OA2+OB2=2OA2=AB2,
∴△OAB为等腰直角三角形,∠AOB=90°,∴∠ASB=∠AOB=45°.
6.B [解析]如图,连接AC,CE.
∵点A,B,C,E都是☉O上的点,∴∠AEC=180°-∠B=58°.
∵,∴∠ACE=∠AEC=58°,∴∠CAE=180°-58°-58°=64°.
∵点A,C,D,E都是☉O上的点,∴∠D=180°-64°=116°.
7.A [解析]如图,连接AC.
∵AB是☉O的直径,
∴∠ACB=90°,∴AC==5.
∵P是(含端点)上任意一点,
∴AC≤AP≤AB,即5≤AP≤13.
8.132° [解析]如图,连接AD.
∵AB为☉O的直径,∴∠ADB=90°.
∵∠ABD=42°,
∴∠A=90°-∠ABD=48°,
∴∠BCD=180°-∠A=132°.
9.解:(1)证明:∵BE=CF,∴,
∴∠BAE=∠CAF.
∵AF⊥BC,∴∠ADC=90°,
∴∠CAF+∠ACD=90°.
∵∠E=∠ACD,∴∠E+∠BAE=90°,
∴∠ABE=90°,
∴AE是☉O的直径.
(2)解法一:如图,连接OC,则∠AOC=2∠ABC.
∵∠ABC=∠CAE,∴∠AOC=2∠CAE.
∵OA=OC,∴∠CAO=∠ACO=∠AOC,
∴∠CAO=∠ACO=45°,∠AOC=90°,∴△AOC是等腰直角三角形.
∵AE=8,∴AO=CO=4,∴AC=4.
解法二:连接OC,CE.∵∠ABC=∠CAE,∠ABC=∠AOC,∠CAE=∠COE,
∴∠AOC=∠COE,∴,∴AC=CE.
由(1),得AE是☉O的直径,∴∠ACE=90°,∴△AEC是等腰直角三角形.
∵AE=8,∴由勾股定理,可得AC=4.
10.D [解析]如图,连接OA.∵☉O的直径CD=12cm,∴OD=OA=OC=6cm.
∵OE∶OC=1∶3,∴OE=2cm.∵AB⊥CD,∴AB=2AE,∠OEA=90°.
在Rt△OAE中,AE==4(cm),∴AB=2AE=8cm.
11.A [解析]如图,设桥拱所在圆的圆心为E,作EF⊥AB,垂足为F,延长EF交圆于点H,连接AE.由垂径定理,知F是AB的中点.由题意,知FH=10-2=8(m),AE=EH,EF=EH-FH.
由勾股定理,得AE2=AF2+EF2=AF2+(AE-FH)2,解得AE=13m.
12.6 [解析]∵P是☉O上的动点(点P与点A,B不重合),OE⊥AP于点E,OF⊥PB于点F,
∴根据垂径定理,知AE=EP,BF=PF,
即E为AP的中点,F为PB的中点,∴EF为△APB的中位线.
又∵AB=12,∴EF=AB=×12=6.
13.B [解析]如图,连接OC.∵OA=OC,∠CAO=60°,∴△AOC为等边三角形,
∴∠AOC=60°,∴∠BOC=∠AOB-∠AOC=140°-60°=80°,则的长=.
14.6π [解析]设扇形的半径为Rcm.∵扇形的圆心角为135°,弧长为3πcm,∴=3π,解得R=4,所以此扇形的面积为=6π(cm2).
15. [解析]由图①得的长+的长=的长.∵半径OA=2cm,∠AOB=120°,∴图②的周长为2×(cm).
16.12π [解析]∵扇形的半径为10cm,做成的圆锥形帽子的高为8cm,∴圆锥的底面半径为=6(cm),∴底面周长为2×6π=12π(cm),∴这张扇形纸板的弧长是12πcm.
17.解:(1)连接BC.由题意,得∠CBA'=30°,O'B=OC',∴∠O'CB=∠CBA'=30°,
∴∠BO'C=120°,∴的长=π.
(2)过点O'作OD'⊥BC于点D,则BD=CD.∵∠O'BC=30°,O'B=10,
∴O'D=O'B=5,∴BD=5,∴BC=2BD=10,
∴S空白=×π×102-(-×10×5)=50π-π+25π+25.
18.D [解析]∵纸片上下折叠A,B两点重合,∴∠BMD=90°.∵纸片沿EF折叠,B,M两点重合,∴∠BNF=90°,∴∠BMD=∠BNF=90°,∴CD∥EF,故①正确;根据垂径定理,知BM垂直平分EF,又∵纸片沿EF折叠,B,M两点重合,∴BN=MN,∴BM,EF互相垂直平分,∴四边形MEBF是菱形,故②正确;如图,连接ME,则ME=MB=2MN,∴∠MEN=30°,
∴∠EMN=90°-30°=60°.又∵AM=ME,∴∠AEM=∠EAM=∠EMN=×60°=30°,
∴∠AEF=∠AEM+∠MEN=30°+30°=60°.同理可求∠AFE=60°,∴∠EAF=60°,∴△AEF是等边三角形,故③正确;设圆的半径为r,则MN=r,EN=r,∴EF=2EN=r,AN=r+r=r,
∴S△AEF∶S圆=(×r×r)∶πr2=3∶4π,故④正确.
综上所述,结论正确的是①②③④,共4个.
19.C [解析]因为∠BOC=40°,所以∠BAC=∠BOC=20°.
20.A [解析]如图,延长BO交☉O于点D,则D为格点,∠BAD=90°,由圆周角定理,得∠APB=∠ADB,∴tan∠APB=tan∠ADB=.
21.A [解析]如图所示,∠A还应有另一个不同的值,当点A在点A'处时,∠A'与∠A互补,则∠A'=180°-65°=115°.
22.(6-4,0) 4π [解析]由题意,得OB=2,OA=6,
∴AB==4,则AC=4,∴OC=AC-OA=4-6,∴点C的坐标为(6-4,0).∵tanA=,∴∠A=30°,
∴S扇形BAC==4π.
23.解:(1)证明:在△AOE和△POC中,
∴△AOE≌△POC(SAS).
(2)∠1+∠C=∠2.理由如下:
∵△AOE≌△POC,∴∠E=∠C.
∵∠1+∠E=∠2,
∴∠1+∠C=∠2.
24.解:发现:连接OM,OA.由题意可知OM=OF=3,AF=8,EF⊥l,
∴OA=.
当点M为线段OA与半圆O的交点时,AM取得最小值,最小值为-3.
当点M与点E重合时,AM取得最大值,最大值为=10.
如图①所示,过点B作BP⊥l,垂足为P,连接OB.
∵∠DAF=60°,∠BAD=90°,
∴∠BAP=30°,∴BP=AB=3,
∴OF=BP=3.
∵BP⊥l,EF⊥l,∴BP∥OF,
∴四边形OBPF为平行四边形,
∴OB∥PF,即OB∥l.
故答案为-3,10,平行.
思考:如图②所示,设半圆O与AD边的另一个交点为G,连接OG,过点O作OH⊥EG于点H.
∵∠DAF=60°,EF⊥l,
∴∠AEF=30°,
∴∠GOF=60°,
∴∠GOE=120°.
∵OH⊥EG,∴EH=HG.
在Rt△OEH中,
∵∠EHO=90°,∠HEO=30°,OE=EF=3,
∴OH=OE·sin∠HEO=3×,EH=OE·cos∠HEO=3×,
∴GE=2EH=2×=3,
∴C重合部分=的长+GE=+3=2π+3,
S重合部分=S扇形GOE-S△GOE=-×3×=3π-.
圆
类型之一 确定圆的条件
1.下列说法中,正确的是( )
A.三点确定一个圆
B.三角形有且只有一个外接圆
C.四边形都有一个外接圆
D.以已知线段长为半径能确定一个圆
2.如图1,AC,BE是☉O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )
A.△ABE
B.△ACF
C.△ABD
D.△ADE
图1
图2
3.如图2,一圆弧过网格中的格点A,B,C,在网格中建立平面直角坐标系,使点A的坐标为(0,3),点C的坐标为(2,3),则该圆弧所在圆的圆心坐标是 .?
类型之二 弧、弦、圆心角与圆周角的关系
4.如图3,点A,B,C,D在☉O上,∠AOC=112°,B是的中点,则∠D的度数是( )
A.56°
B.35°
C.38°
D.28°
图3
图4
5.如图4,点A,B,S在圆上,若弦AB的长度等于圆半径的倍,则∠ASB的度数是( )
A.22.5°
B.30°
C.45°
D.60°
6.如图5,点A,B,C,D,E都是☉O上的点,,∠B=122°,则∠D的度数为( )
A.58°
B.116°
C.122°
D.128°
图5
图6
7.[2020·秦皇岛期末]
如图6,AB是☉O的直径,BC是弦,P是(含端点)上任意一点,若AB=13,BC=12,则AP的长不可能是( )
A.4
B.5
C.12
D.13
8.[2020·唐山丰润区期末]
如图7,AB为☉O的直径,点C,D在☉O上,若∠ABD=42°,则∠BCD的度数是 .?
图7
9.已知:如图8,△ABC内接于☉O,AF是☉O的弦,AF⊥BC,垂足为D,E为上一点,且BE=CF.
(1)求证:AE是☉O的直径;
(2)若∠ABC=∠CAE,AE=8,求AC的长.
图8
类型之三 利用垂径定理进行计算
10.[2020·唐山期末]
如图9,☉O的直径CD=12cm,AB是☉O的弦,AB⊥CD,垂足为E,OE∶OC=1∶3,则AB的长为( )
A.2cm
B.4cm
C.6cm
D.8cm
图9
图10
11.图10是某座天桥的设计图,设计数据如图所示,桥拱是圆弧形,则桥拱的半径为( )
A.13m
B.15m
C.20m
D.26m
12.如图11,A,B是☉O上的两点,AB=12,P是☉O上的动点(点P与点A,B不重合),连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF= .?
图11
类型之四 弧长及扇形面积的计算
13.如图12,在扇形AOB中,AC为弦,∠AOB=140°,∠CAO=60°,OA=6,则的长为( )
图12
A.
B.
C.2π
D.2π
14.一个扇形的圆心角为135°,弧长为3πcm,则此扇形的面积是 cm2.?
15.如图13,图①是由若干个相同的图形(图②)组成的美丽图案的一部分,图②中,图形的相关数据如下:半径OA=2cm,∠AOB=120°,则图②的周长为 cm(结果保留π).?
图13
图14
16.如图14,用一张半径为10cm的扇形纸板做一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的高为8cm,那么这张扇形纸板的弧长是 cm.?
17.[2020·唐山期末]
将两张半径均为10的半圆形的纸片完全重合叠放在一起,上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图15所示的图形,与直径AB交于点C,连接点C与圆心O'.
(1)求的长;
(2)求图中下面这张半圆形纸片未被上面这张纸片遮挡部分的面积S空白.
图15
类型之五 数学活动
18.一张圆形纸片,嘉琪进行了如下连续操作:
(1)将圆形纸片左右对折,折痕为AB,如图②所示.
(2)将圆形纸片上下折叠,使A,B两点重合,折痕CD与AB相交于点M,如图③所示.
(3)将圆形纸片沿EF折叠,使B,M两点重合,折痕EF与AB相交于点N,如图④所示.
(4)连接AE,AF,如图⑤所示.
经过以上操作嘉琪得到了以下结论:①CD∥EF;②四边形MEBF是菱形;③△AEF为等边三角形;④S△AEF∶S圆=3∶4π.以上结论正确的有( )
A.1个
B.2个
C.3个
D.4个
图16
【河北题型训练】
19.[2020·唐山期末]
如图17,把一个量角器放在∠BAC的上面,点B恰好在量角器上40°的位置,则∠BAC的度数是( )
A.40°
B.80°
C.20°
D.10°
图17
图18
20.[2020·石家庄模拟]
如图18,在6×6的正方形网格中,☉O经过格点A,B,C,点P是上任意一点,连接AP,BP,则tan∠APB的值为( )
A.
B.
C.
D.
21.[2020·河北]
有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆☉O,连接OB,OC.如图19,由∠BOC=2∠A=130°,得∠A=
65°.而淇淇说:“嘉嘉考虑得不周全,∠A还应有另一个不同的值.”下列判断正确的是( )
A.淇淇说得对,且∠A的另一个值是115°
B.淇淇说得不对,∠A就得65°
C.嘉嘉求的结果不对,∠A应得50°
D.两人都不对,∠A应有3个不同的值
图19
图20
22.[2020·石家庄模拟]
如图20,在平面直角坐标系中,A(6,0),B(0,2),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C的坐标为 ,扇形BAC的面积为 .?
23.[2020·河北节选]
如图21,O为AB的中点,分别延长OA到点C,OB到点D,使OC=OD.以点O为圆心,分别以OA,OC为半径在CD上方作两个半圆.点P为小半圆上任一点(不与点A,B重合),连接OP并延长交大半圆于点E,连接AE,CP.
(1)求证:△AOE≌△POC;
(2)写出∠1,∠2和∠C三者之间的数量关系,并说明理由.
图21
24.[2020·石家庄正定县期末]
如图22,在矩形ABCD中,AB=6,BC=8,点A在直线l上,AD与直线l相交所得的锐角为60°.点F在直线l上,AF=8,EF⊥直线l,垂足为F,且EF=6,以EF为直径,在EF的左侧作半圆O,M是半圆O上任一点.
发现:AM的最小值为 ,AM的最大值为 ,OB与直线l的位置关系是 .?
思考:矩形ABCD保持不动,半圆O沿直线l向左平移,当点E落在AD边上时,求半圆与矩形重合部分的周长和面积.
图22
答案
1.B
2.B [解析]各选项中,只有△ACF的三个顶点不都在圆上,故外心不是点O的是△ACF.
3.(1,0) [解析]如图,分别作弦AB,AC的垂直平分线,交于点D(1,0),所以该圆弧所在圆的圆心坐标是(1,0).
4.D [解析]如图,连接OB.∵B是的中点,∴∠AOB=∠AOC=56°.由圆周角定理,得∠D=∠AOB=28°.
5.C [解析]如图,设圆心为O,连接OA,OB.∵弦AB的长度等于圆半径的倍,即AB=OA.∵OA=OB,
∴OA2+OB2=2OA2=AB2,
∴△OAB为等腰直角三角形,∠AOB=90°,∴∠ASB=∠AOB=45°.
6.B [解析]如图,连接AC,CE.
∵点A,B,C,E都是☉O上的点,∴∠AEC=180°-∠B=58°.
∵,∴∠ACE=∠AEC=58°,∴∠CAE=180°-58°-58°=64°.
∵点A,C,D,E都是☉O上的点,∴∠D=180°-64°=116°.
7.A [解析]如图,连接AC.
∵AB是☉O的直径,
∴∠ACB=90°,∴AC==5.
∵P是(含端点)上任意一点,
∴AC≤AP≤AB,即5≤AP≤13.
8.132° [解析]如图,连接AD.
∵AB为☉O的直径,∴∠ADB=90°.
∵∠ABD=42°,
∴∠A=90°-∠ABD=48°,
∴∠BCD=180°-∠A=132°.
9.解:(1)证明:∵BE=CF,∴,
∴∠BAE=∠CAF.
∵AF⊥BC,∴∠ADC=90°,
∴∠CAF+∠ACD=90°.
∵∠E=∠ACD,∴∠E+∠BAE=90°,
∴∠ABE=90°,
∴AE是☉O的直径.
(2)解法一:如图,连接OC,则∠AOC=2∠ABC.
∵∠ABC=∠CAE,∴∠AOC=2∠CAE.
∵OA=OC,∴∠CAO=∠ACO=∠AOC,
∴∠CAO=∠ACO=45°,∠AOC=90°,∴△AOC是等腰直角三角形.
∵AE=8,∴AO=CO=4,∴AC=4.
解法二:连接OC,CE.∵∠ABC=∠CAE,∠ABC=∠AOC,∠CAE=∠COE,
∴∠AOC=∠COE,∴,∴AC=CE.
由(1),得AE是☉O的直径,∴∠ACE=90°,∴△AEC是等腰直角三角形.
∵AE=8,∴由勾股定理,可得AC=4.
10.D [解析]如图,连接OA.∵☉O的直径CD=12cm,∴OD=OA=OC=6cm.
∵OE∶OC=1∶3,∴OE=2cm.∵AB⊥CD,∴AB=2AE,∠OEA=90°.
在Rt△OAE中,AE==4(cm),∴AB=2AE=8cm.
11.A [解析]如图,设桥拱所在圆的圆心为E,作EF⊥AB,垂足为F,延长EF交圆于点H,连接AE.由垂径定理,知F是AB的中点.由题意,知FH=10-2=8(m),AE=EH,EF=EH-FH.
由勾股定理,得AE2=AF2+EF2=AF2+(AE-FH)2,解得AE=13m.
12.6 [解析]∵P是☉O上的动点(点P与点A,B不重合),OE⊥AP于点E,OF⊥PB于点F,
∴根据垂径定理,知AE=EP,BF=PF,
即E为AP的中点,F为PB的中点,∴EF为△APB的中位线.
又∵AB=12,∴EF=AB=×12=6.
13.B [解析]如图,连接OC.∵OA=OC,∠CAO=60°,∴△AOC为等边三角形,
∴∠AOC=60°,∴∠BOC=∠AOB-∠AOC=140°-60°=80°,则的长=.
14.6π [解析]设扇形的半径为Rcm.∵扇形的圆心角为135°,弧长为3πcm,∴=3π,解得R=4,所以此扇形的面积为=6π(cm2).
15. [解析]由图①得的长+的长=的长.∵半径OA=2cm,∠AOB=120°,∴图②的周长为2×(cm).
16.12π [解析]∵扇形的半径为10cm,做成的圆锥形帽子的高为8cm,∴圆锥的底面半径为=6(cm),∴底面周长为2×6π=12π(cm),∴这张扇形纸板的弧长是12πcm.
17.解:(1)连接BC.由题意,得∠CBA'=30°,O'B=OC',∴∠O'CB=∠CBA'=30°,
∴∠BO'C=120°,∴的长=π.
(2)过点O'作OD'⊥BC于点D,则BD=CD.∵∠O'BC=30°,O'B=10,
∴O'D=O'B=5,∴BD=5,∴BC=2BD=10,
∴S空白=×π×102-(-×10×5)=50π-π+25π+25.
18.D [解析]∵纸片上下折叠A,B两点重合,∴∠BMD=90°.∵纸片沿EF折叠,B,M两点重合,∴∠BNF=90°,∴∠BMD=∠BNF=90°,∴CD∥EF,故①正确;根据垂径定理,知BM垂直平分EF,又∵纸片沿EF折叠,B,M两点重合,∴BN=MN,∴BM,EF互相垂直平分,∴四边形MEBF是菱形,故②正确;如图,连接ME,则ME=MB=2MN,∴∠MEN=30°,
∴∠EMN=90°-30°=60°.又∵AM=ME,∴∠AEM=∠EAM=∠EMN=×60°=30°,
∴∠AEF=∠AEM+∠MEN=30°+30°=60°.同理可求∠AFE=60°,∴∠EAF=60°,∴△AEF是等边三角形,故③正确;设圆的半径为r,则MN=r,EN=r,∴EF=2EN=r,AN=r+r=r,
∴S△AEF∶S圆=(×r×r)∶πr2=3∶4π,故④正确.
综上所述,结论正确的是①②③④,共4个.
19.C [解析]因为∠BOC=40°,所以∠BAC=∠BOC=20°.
20.A [解析]如图,延长BO交☉O于点D,则D为格点,∠BAD=90°,由圆周角定理,得∠APB=∠ADB,∴tan∠APB=tan∠ADB=.
21.A [解析]如图所示,∠A还应有另一个不同的值,当点A在点A'处时,∠A'与∠A互补,则∠A'=180°-65°=115°.
22.(6-4,0) 4π [解析]由题意,得OB=2,OA=6,
∴AB==4,则AC=4,∴OC=AC-OA=4-6,∴点C的坐标为(6-4,0).∵tanA=,∴∠A=30°,
∴S扇形BAC==4π.
23.解:(1)证明:在△AOE和△POC中,
∴△AOE≌△POC(SAS).
(2)∠1+∠C=∠2.理由如下:
∵△AOE≌△POC,∴∠E=∠C.
∵∠1+∠E=∠2,
∴∠1+∠C=∠2.
24.解:发现:连接OM,OA.由题意可知OM=OF=3,AF=8,EF⊥l,
∴OA=.
当点M为线段OA与半圆O的交点时,AM取得最小值,最小值为-3.
当点M与点E重合时,AM取得最大值,最大值为=10.
如图①所示,过点B作BP⊥l,垂足为P,连接OB.
∵∠DAF=60°,∠BAD=90°,
∴∠BAP=30°,∴BP=AB=3,
∴OF=BP=3.
∵BP⊥l,EF⊥l,∴BP∥OF,
∴四边形OBPF为平行四边形,
∴OB∥PF,即OB∥l.
故答案为-3,10,平行.
思考:如图②所示,设半圆O与AD边的另一个交点为G,连接OG,过点O作OH⊥EG于点H.
∵∠DAF=60°,EF⊥l,
∴∠AEF=30°,
∴∠GOF=60°,
∴∠GOE=120°.
∵OH⊥EG,∴EH=HG.
在Rt△OEH中,
∵∠EHO=90°,∠HEO=30°,OE=EF=3,
∴OH=OE·sin∠HEO=3×,EH=OE·cos∠HEO=3×,
∴GE=2EH=2×=3,
∴C重合部分=的长+GE=+3=2π+3,
S重合部分=S扇形GOE-S△GOE=-×3×=3π-.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
