1.4空间向量的应用-【新教材】人教A版(2019)高中数学选择性必修第一册课后练习(Word含答案)
文档属性
| 名称 | 1.4空间向量的应用-【新教材】人教A版(2019)高中数学选择性必修第一册课后练习(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 313.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 22:14:49 | ||
图片预览




文档简介
1.4空间向量的应用
一、单选题
1.在空间直角坐标系中,点false关于x轴的对称点的坐标为N,已知点false,则false( )
A.false B.false C.false D.false
2.已知false,false,false,若false,且false平面false,则false( )
A.false B.false C.false D.false
3.二面角false-false-false为60°,A、B是棱false上的两点,false、false分别在半平面false内,false,false,且false,false,则false的长为( )
A.false B.false C.false D.false
4.已知直线false的方向向量为false,平面false的法向量为false,若false, false,则直线false与平面false的位置关系是( )
A.垂直 B.平行 C.相交但不垂直 D.直线false在平面false内或直线false与平面false平行
5.直三棱柱false中,false,false,则异面直线false和false所成角的余弦值为( )
A.false B.false C.false D.false
6.已知点false是平行四边形false所在的平面外一点,如果false,false,false.对于结论:①false;②false;③false是平面false的法向量;④false.其中正确的是( )
A.②④ B.②③ C.①③ D.①②
7.已知false是各棱长均等于false的正三棱柱,false是侧棱false的中点,则平面false与平面false所成的锐二面角为( )
A.45° B.60° C.75° D.30°
8.如图,二面角false的大小为false,false,false分别在平面false,false内,false,false,false,false,false,则false( )
A.false B.false
C.false D.false
二、填空题
9.空间坐标系中,过点false且与直线false垂直的平面方程为_______.
10.若直线false的方向向量为false.平面false的法向量为false,则直线false与平面false的关系为________.
11.已知三点A(1,1,0),B(1,0,1),C(0,1,1),则平面ABC的单位法向量为_______
12.在四棱锥false中,底面false为平行四边形,false平面false,false,false,false,false,则当false变化时,直线false与平面false所成角的取值范围是__________.
三、解答题
13.已知三棱锥 M?ABC 中, MA=MB=MC=AC=22 , AB=BC=2 ,O为AC的中点,点N在边BC上,且 BN=23BC .
(1)求证: BO⊥ 平面AMC;
(2)求二面角 N?AM?C 的余弦值.
14.如图,在三棱柱 ABC?A1B1C1 中, ∠ACB=∠C1CB=90? , ∠A1AC=60? , D 、 E 分别为 A1A 和 B1C1 的中点,且 AA1=AC=BC .
(1)求证: A1E// 平面 BC1D ;
(2)求平面 BC1D 与平面 ABC 所成锐二面角的余弦值.
15.如图,在三棱柱 ABC?A1B1C1 中, AA1⊥ 底面 ABC , ΔABC 是边长为2的正三角形, AA1=3 ,D,E分别为 AB , BC 的中点.
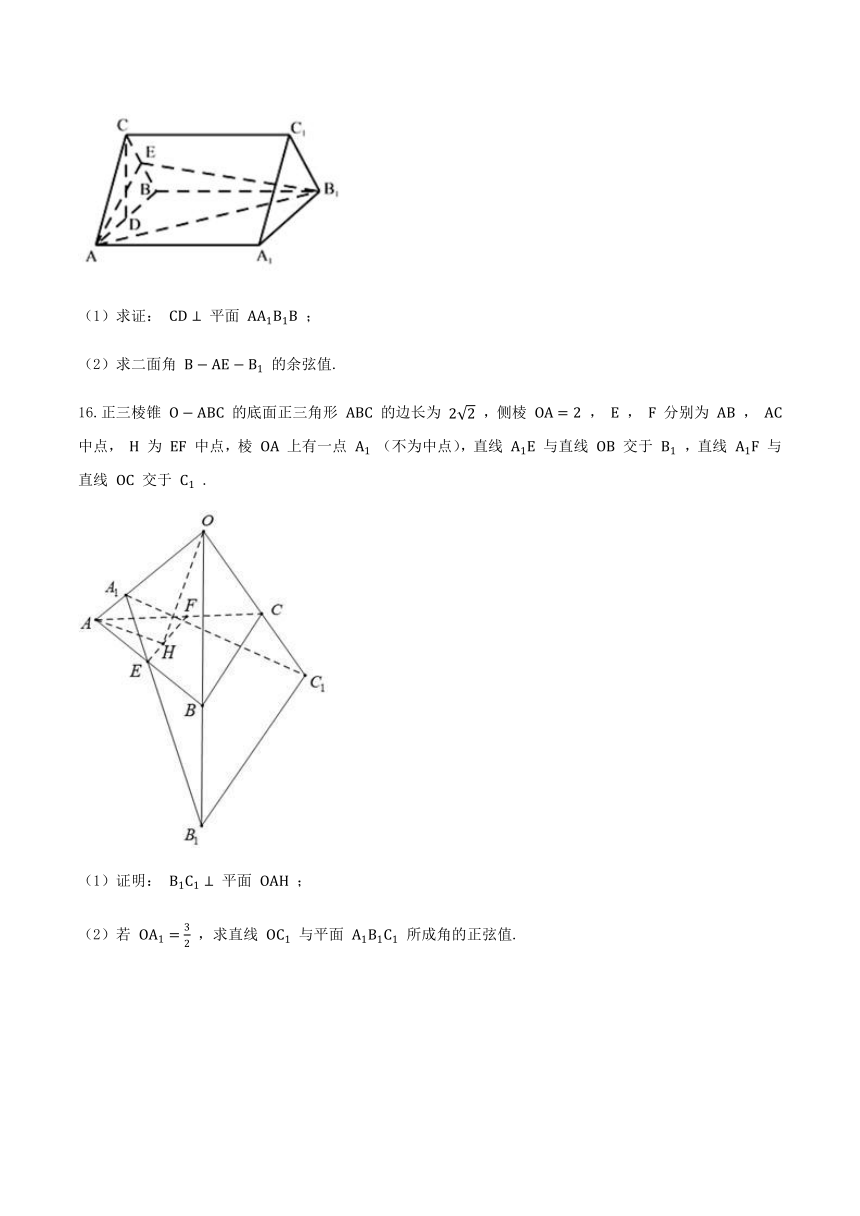
(1)求证: CD⊥ 平面 AA1B1B ;
(2)求二面角 B?AE?B1 的余弦值.
16.正三棱锥 O?ABC 的底面正三角形 ABC 的边长为 22 ,侧棱 OA=2 , E , F 分别为 AB , AC 中点, H 为 EF 中点,棱 OA 上有一点 A1 (不为中点),直线 A1E 与直线 OB 交于 B1 ,直线 A1F 与直线 OC 交于 C1 .
(1)证明: B1C1⊥ 平面 OAH ;
(2)若 OA1=32 ,求直线 OC1 与平面 A1B1C1 所成角的正弦值.
参考答案
A2.D3.D4.D5.C6.B7.A8.A9.false10.false11.(false,false,false)或(-false,-false,-false)12.false
13.【答案】 (1)证明:连接OM,
在△ABC中,∵AB=BC=2,AC=2 2 ,
∴∠ABC=90° ,BO= 2 ,OB⊥AC
在△MAC中,∵MA=MC=AC=2 2 ,O为AC的中点,
∴OM⊥AC,且OM= 6
在△MOB中,∵BO= 2 ,OM= 6 ,MB=2 2 ?,
∴BO2+OM2= MB2 , ∴OB⊥OM
∵AC∩OM=O,AC ? 平面AMC,OM ? 平面AMC,
∴OB⊥平面AMC
(2)解:由(1)知OB,OC,OM两两垂直,以点O为坐标原点,分别以OB,OC,OM所在直线为x轴、y轴、z轴建立空间直角坐标系O-xyz,如图。
∵MA=MB=MC=AC=2 2 ,AB=BC=2,
∴A(0,- 2 ,0) ,B( 2 ,0,0) ,M(0,0, 6 ),C(0, 2 ,0)
∵ BN = 23 BC ,∴N( 23 , 223 ,0)
∴ AN =( 23 , 523 ,0) , AM =(0, 2 , 6 ), OB =( 2 ,0,0)
设平面MAN的法向量为n=(x,y,z),
则 {AN·n=(23,523,0)·(x,y,z)=23x+523y=0AM·n=(0,2,6)·(x,y,z)=2y+523z=0
令y= 3 ,则z=-1,x=-5 3 ,得n=(-5 3 , 3 ,-1)
∵BO⊥平面AMC,
∴ OB =( 2 ,0,0)为平面AMC的-一个法向量,
∴n=(-5 3 , 3 ,-1)与 OB =( 2 ,0,0)所成角的余弦值
cos∴二面角N-AM-C的余弦值为 ?5379
【解析】(1)利用已知条件结合三棱锥的结构特征,再利用中点的性质结合线线垂直,从而利用线面垂直的判定定理证出线面垂直。
(2) 由(1)知OB,OC,OM两两垂直,以点O为坐标原点,分别以OB,OC,OM所在直线为x轴、y轴、z轴建立空间直角坐标系O-xyz, 再利用已知条件结合空间向量的方法求出二面角 N?AM?C 的平面角的余弦值。
14.【答案】 (1)证明:如图 1 ,取线段 BC1 的中点 F ,连接 EF 、 DF ,
∵E 为 B1C1 的中点, ∴EF//BB1 且 EF=12BB1 ,
又 D 为 AA1 的中点, ∴A1D//BB1 且 A1D=12BB1 , ∴EF//A1D 且 EF=A1D ,
∴ 四边形 A1DFE 为平行四边形, ∴A1E//DF ,
又 DF? 平面 BC1D , A1E? 平面 BC1D , ∴A1E// 平面 BC1D
(2)解:作 A1O⊥AC 于点 O ,由 ∠A1AC=60? ,得 ∠AA1O=30? ,
∴AO=12AA1=12AC ,即 O 为 AC 的中点,
∵∠ACB=∠C1CB=90? , ∴BC⊥AC , BC⊥CC1 ,
又 AC∩CC1=C , ∴BC⊥ 平面 A1ACC1 , ∵A1O? 平面 A1ACC1 ,从而有 BC⊥A1O ,
又 A1O⊥AC , AC∩BC=C , ∴A1O⊥ 平面 ABC ,
故可以点 O 为坐标原点,射线 OA 、 OA1 分别为 x 轴、 z 轴的正半轴,以平行于 BC 的直线为 y 轴,建立空间直角坐标系,如图 2 ,
令 AA1=AC=BC=2a ,则 A(a,0,0) 、 B(?a,2a,0) 、 A1(0,0,3a) 、 C1(?2a,0,3a) 、 D(12a,0,32a) ,
∴BD=(32a,?2a,32a) , C1D=(52a,0,?32a) ,
设平面 BC1D 的一个法向量为 m=(x,y,z) ,则 {m?BD=32x?2y+32z=0m?C1D=52x?32z=0 ,
取 z=5 ,则 x=3 , y=23 ,可得 m=(3,23,5) ,
又平面 ABC 的一个法向量为 OA1=(0,0,3a) ,
设平面 BC1D 与平面 ABC 所成锐二面角为 θ ,则 cosθ=|m?OA1||m|?|OA1|=53a40?3a=104 ,
因此,平面 BC1D 与平面 ABC 所成锐二面角的余弦值为 104
【解析】(1)先根据 EF//BB1 且 EF=12BB1 , A1D//BB1 且 A1D=12BB1 可知四边形 A1DFE 为平行四边形,由此 A1E//DF ,进而得证;(2)先证明 A1O⊥ 平面 ABC ,由此可以 O 为坐标原点,射线 OA 、 OA1 分别为 x 轴、 z 轴的正半轴,以平行于 BC 的直线为 y 轴,建立空间直角坐标系,求出平面 BC1D 与平面 ABC 的法向量,再利用向量的夹角公式得解.
15.【答案】 (1)证明:在三棱柱 ABC?A1B1C1 中,因为 AA1⊥ 底面 ABC , CD? 平面 ABC ,
所以 AA1⊥CD .又 ΔABC 为等边三角形,D为 AB 的中点,所以 CD⊥AD .
因为 AB∩AA1=A ,所以 CD⊥ 平面 AA1B1B .
(2)解:取 A1B1 中点F,连结 DF ,则因为D,F分别为 AB , A1B1 的中点,
所以 DF⊥AB .由(1)知 CD⊥AB , CD⊥DF ,
如图建立空间直角坐标系 D?xyz ,
由题意得 A(1,0,0) , B(?1,0,0) , C(0,0,3) ,
A1=(1,3,0) , B1(?1,3,0) , C1(0,3,3) ,
D(0,0,0) , E(?32,0,32) , AE1=(?32,0,32) , AB1=(?2,3,0) ,
设平面 AB1E 的法向量 n=(x,y,z) , AE=(?32,0,32) , AB1=(?2,3,0) ,
则 {n?AE=?32x+32z=0n?AB1=?2x+3y=0 ,令 x=1 ,则 n=(1,23,3) .
平面 BAE 法向量 AA1=(0,3,0) .
因为 cos?AA1,n?=AA1?n|AA1|?|n|=1010 .
【解析】(1)利用线面垂直的性质可得 AA1⊥CD ,再由 CD⊥AD ,根据线面垂直的判定定理即可证出.(2)以 D 为原点,以 DA,DF,DC 为 x,y,z 轴,建立空间直角坐标系 D?xyz ,求出平面 AB1E 的一个法向量, 平面 BAE 的一个法向量,利用空间向量的数量积即可求解.
16.【答案】 (1)证明:由题意可得 EF 是正三角形 ABC 的中位线,所以 EF//BC , EF? 面 OBC , BC? 面 OBC ,可得 EF// 面 OBC , EF? 面 A1B1C1 ,面 A1B1C1∩ 面 OBC=B1C1 ,则 EF//B1C1 ,
在正三角形 AEF 中, H 为 EF 中点,可得 EF⊥AH ,即 B1C1⊥AH ,
底面正三角形 ABC 的边长为 22 ,侧棱长为 2 ,可得三条侧棱两两垂直,
即 OA⊥OB,OA⊥OC , OB∩OC=O ,可得 OA⊥ 面 OBC ,则 OA⊥ B1C1 ,
又 OA∩AH=A ,由线面垂直的判定定理可得 B1C1⊥ 平面 OAH
(2)解:由已知可得三条侧棱两两垂直,以直线 OA,OB,OC 分别为 x,y,z 轴建立空间直角坐标系,
则 A(2,0,0),B(0,0,2),C(0,2,0),E(1,0,1),F(1,1,0),H(1,12,12) , A1(32,0,0) ,
设 B1(0,0,t) ,则 A1E=(?12,0,1),EB1=(?1,0,t?1) ,由 A1E 与 EB1 共线得 A1E=λEB1 ,
得 {?12=?λ1=λ(t?1) ,解得 t=3 ,所以 B1(0,0,3) ,同理得 C1(0,3,0) ,
可得 A1B1=(?32,0,3),A1C1=(?32,3,0) ,设平面 A1B1C1 的一个法向量为 n=(x,y,z) ,
{?32x+3z=0?32x+3y=0 ?,令 x=2 ,得 y=z=1 ,即 n=(2,1,1) , OC1=(0,3,0) ,
设直线 OC1 与平面 A1B1C1 所成角为 θ ,则 sinθ=|cos?n,OC1?|=|n?OC1||n||OC1|=33×6=66 ,
则直线 OC1 与平面 A1B1C1 所成角的正弦值为 66
【解析】(1)根据题意证明 EF// 面 OBC ,由线面平行的性质定理得 EF//B1C1 ,由已知可得 EF⊥AH ,即得 B1C1⊥AH ,再证明 OA⊥ 面 OBC ,得 OA⊥ B1C1 ,由线面垂直的判定定理即可得到证明.(2)以直线 OA,OB,OC 分别为 x,y,z 轴建立空间直角坐标系,求 OC1 的坐标和平面 A1B1C1 的法向量,由线面角的向量公式进行计算即可得到答案.
一、单选题
1.在空间直角坐标系中,点false关于x轴的对称点的坐标为N,已知点false,则false( )
A.false B.false C.false D.false
2.已知false,false,false,若false,且false平面false,则false( )
A.false B.false C.false D.false
3.二面角false-false-false为60°,A、B是棱false上的两点,false、false分别在半平面false内,false,false,且false,false,则false的长为( )
A.false B.false C.false D.false
4.已知直线false的方向向量为false,平面false的法向量为false,若false, false,则直线false与平面false的位置关系是( )
A.垂直 B.平行 C.相交但不垂直 D.直线false在平面false内或直线false与平面false平行
5.直三棱柱false中,false,false,则异面直线false和false所成角的余弦值为( )
A.false B.false C.false D.false
6.已知点false是平行四边形false所在的平面外一点,如果false,false,false.对于结论:①false;②false;③false是平面false的法向量;④false.其中正确的是( )
A.②④ B.②③ C.①③ D.①②
7.已知false是各棱长均等于false的正三棱柱,false是侧棱false的中点,则平面false与平面false所成的锐二面角为( )
A.45° B.60° C.75° D.30°
8.如图,二面角false的大小为false,false,false分别在平面false,false内,false,false,false,false,false,则false( )
A.false B.false
C.false D.false
二、填空题
9.空间坐标系中,过点false且与直线false垂直的平面方程为_______.
10.若直线false的方向向量为false.平面false的法向量为false,则直线false与平面false的关系为________.
11.已知三点A(1,1,0),B(1,0,1),C(0,1,1),则平面ABC的单位法向量为_______
12.在四棱锥false中,底面false为平行四边形,false平面false,false,false,false,false,则当false变化时,直线false与平面false所成角的取值范围是__________.
三、解答题
13.已知三棱锥 M?ABC 中, MA=MB=MC=AC=22 , AB=BC=2 ,O为AC的中点,点N在边BC上,且 BN=23BC .
(1)求证: BO⊥ 平面AMC;
(2)求二面角 N?AM?C 的余弦值.
14.如图,在三棱柱 ABC?A1B1C1 中, ∠ACB=∠C1CB=90? , ∠A1AC=60? , D 、 E 分别为 A1A 和 B1C1 的中点,且 AA1=AC=BC .
(1)求证: A1E// 平面 BC1D ;
(2)求平面 BC1D 与平面 ABC 所成锐二面角的余弦值.
15.如图,在三棱柱 ABC?A1B1C1 中, AA1⊥ 底面 ABC , ΔABC 是边长为2的正三角形, AA1=3 ,D,E分别为 AB , BC 的中点.
(1)求证: CD⊥ 平面 AA1B1B ;
(2)求二面角 B?AE?B1 的余弦值.
16.正三棱锥 O?ABC 的底面正三角形 ABC 的边长为 22 ,侧棱 OA=2 , E , F 分别为 AB , AC 中点, H 为 EF 中点,棱 OA 上有一点 A1 (不为中点),直线 A1E 与直线 OB 交于 B1 ,直线 A1F 与直线 OC 交于 C1 .
(1)证明: B1C1⊥ 平面 OAH ;
(2)若 OA1=32 ,求直线 OC1 与平面 A1B1C1 所成角的正弦值.
参考答案
A2.D3.D4.D5.C6.B7.A8.A9.false10.false11.(false,false,false)或(-false,-false,-false)12.false
13.【答案】 (1)证明:连接OM,
在△ABC中,∵AB=BC=2,AC=2 2 ,
∴∠ABC=90° ,BO= 2 ,OB⊥AC
在△MAC中,∵MA=MC=AC=2 2 ,O为AC的中点,
∴OM⊥AC,且OM= 6
在△MOB中,∵BO= 2 ,OM= 6 ,MB=2 2 ?,
∴BO2+OM2= MB2 , ∴OB⊥OM
∵AC∩OM=O,AC ? 平面AMC,OM ? 平面AMC,
∴OB⊥平面AMC
(2)解:由(1)知OB,OC,OM两两垂直,以点O为坐标原点,分别以OB,OC,OM所在直线为x轴、y轴、z轴建立空间直角坐标系O-xyz,如图。
∵MA=MB=MC=AC=2 2 ,AB=BC=2,
∴A(0,- 2 ,0) ,B( 2 ,0,0) ,M(0,0, 6 ),C(0, 2 ,0)
∵ BN = 23 BC ,∴N( 23 , 223 ,0)
∴ AN =( 23 , 523 ,0) , AM =(0, 2 , 6 ), OB =( 2 ,0,0)
设平面MAN的法向量为n=(x,y,z),
则 {AN·n=(23,523,0)·(x,y,z)=23x+523y=0AM·n=(0,2,6)·(x,y,z)=2y+523z=0
令y= 3 ,则z=-1,x=-5 3 ,得n=(-5 3 , 3 ,-1)
∵BO⊥平面AMC,
∴ OB =( 2 ,0,0)为平面AMC的-一个法向量,
∴n=(-5 3 , 3 ,-1)与 OB =( 2 ,0,0)所成角的余弦值
cos
【解析】(1)利用已知条件结合三棱锥的结构特征,再利用中点的性质结合线线垂直,从而利用线面垂直的判定定理证出线面垂直。
(2) 由(1)知OB,OC,OM两两垂直,以点O为坐标原点,分别以OB,OC,OM所在直线为x轴、y轴、z轴建立空间直角坐标系O-xyz, 再利用已知条件结合空间向量的方法求出二面角 N?AM?C 的平面角的余弦值。
14.【答案】 (1)证明:如图 1 ,取线段 BC1 的中点 F ,连接 EF 、 DF ,
∵E 为 B1C1 的中点, ∴EF//BB1 且 EF=12BB1 ,
又 D 为 AA1 的中点, ∴A1D//BB1 且 A1D=12BB1 , ∴EF//A1D 且 EF=A1D ,
∴ 四边形 A1DFE 为平行四边形, ∴A1E//DF ,
又 DF? 平面 BC1D , A1E? 平面 BC1D , ∴A1E// 平面 BC1D
(2)解:作 A1O⊥AC 于点 O ,由 ∠A1AC=60? ,得 ∠AA1O=30? ,
∴AO=12AA1=12AC ,即 O 为 AC 的中点,
∵∠ACB=∠C1CB=90? , ∴BC⊥AC , BC⊥CC1 ,
又 AC∩CC1=C , ∴BC⊥ 平面 A1ACC1 , ∵A1O? 平面 A1ACC1 ,从而有 BC⊥A1O ,
又 A1O⊥AC , AC∩BC=C , ∴A1O⊥ 平面 ABC ,
故可以点 O 为坐标原点,射线 OA 、 OA1 分别为 x 轴、 z 轴的正半轴,以平行于 BC 的直线为 y 轴,建立空间直角坐标系,如图 2 ,
令 AA1=AC=BC=2a ,则 A(a,0,0) 、 B(?a,2a,0) 、 A1(0,0,3a) 、 C1(?2a,0,3a) 、 D(12a,0,32a) ,
∴BD=(32a,?2a,32a) , C1D=(52a,0,?32a) ,
设平面 BC1D 的一个法向量为 m=(x,y,z) ,则 {m?BD=32x?2y+32z=0m?C1D=52x?32z=0 ,
取 z=5 ,则 x=3 , y=23 ,可得 m=(3,23,5) ,
又平面 ABC 的一个法向量为 OA1=(0,0,3a) ,
设平面 BC1D 与平面 ABC 所成锐二面角为 θ ,则 cosθ=|m?OA1||m|?|OA1|=53a40?3a=104 ,
因此,平面 BC1D 与平面 ABC 所成锐二面角的余弦值为 104
【解析】(1)先根据 EF//BB1 且 EF=12BB1 , A1D//BB1 且 A1D=12BB1 可知四边形 A1DFE 为平行四边形,由此 A1E//DF ,进而得证;(2)先证明 A1O⊥ 平面 ABC ,由此可以 O 为坐标原点,射线 OA 、 OA1 分别为 x 轴、 z 轴的正半轴,以平行于 BC 的直线为 y 轴,建立空间直角坐标系,求出平面 BC1D 与平面 ABC 的法向量,再利用向量的夹角公式得解.
15.【答案】 (1)证明:在三棱柱 ABC?A1B1C1 中,因为 AA1⊥ 底面 ABC , CD? 平面 ABC ,
所以 AA1⊥CD .又 ΔABC 为等边三角形,D为 AB 的中点,所以 CD⊥AD .
因为 AB∩AA1=A ,所以 CD⊥ 平面 AA1B1B .
(2)解:取 A1B1 中点F,连结 DF ,则因为D,F分别为 AB , A1B1 的中点,
所以 DF⊥AB .由(1)知 CD⊥AB , CD⊥DF ,
如图建立空间直角坐标系 D?xyz ,
由题意得 A(1,0,0) , B(?1,0,0) , C(0,0,3) ,
A1=(1,3,0) , B1(?1,3,0) , C1(0,3,3) ,
D(0,0,0) , E(?32,0,32) , AE1=(?32,0,32) , AB1=(?2,3,0) ,
设平面 AB1E 的法向量 n=(x,y,z) , AE=(?32,0,32) , AB1=(?2,3,0) ,
则 {n?AE=?32x+32z=0n?AB1=?2x+3y=0 ,令 x=1 ,则 n=(1,23,3) .
平面 BAE 法向量 AA1=(0,3,0) .
因为 cos?AA1,n?=AA1?n|AA1|?|n|=1010 .
【解析】(1)利用线面垂直的性质可得 AA1⊥CD ,再由 CD⊥AD ,根据线面垂直的判定定理即可证出.(2)以 D 为原点,以 DA,DF,DC 为 x,y,z 轴,建立空间直角坐标系 D?xyz ,求出平面 AB1E 的一个法向量, 平面 BAE 的一个法向量,利用空间向量的数量积即可求解.
16.【答案】 (1)证明:由题意可得 EF 是正三角形 ABC 的中位线,所以 EF//BC , EF? 面 OBC , BC? 面 OBC ,可得 EF// 面 OBC , EF? 面 A1B1C1 ,面 A1B1C1∩ 面 OBC=B1C1 ,则 EF//B1C1 ,
在正三角形 AEF 中, H 为 EF 中点,可得 EF⊥AH ,即 B1C1⊥AH ,
底面正三角形 ABC 的边长为 22 ,侧棱长为 2 ,可得三条侧棱两两垂直,
即 OA⊥OB,OA⊥OC , OB∩OC=O ,可得 OA⊥ 面 OBC ,则 OA⊥ B1C1 ,
又 OA∩AH=A ,由线面垂直的判定定理可得 B1C1⊥ 平面 OAH
(2)解:由已知可得三条侧棱两两垂直,以直线 OA,OB,OC 分别为 x,y,z 轴建立空间直角坐标系,
则 A(2,0,0),B(0,0,2),C(0,2,0),E(1,0,1),F(1,1,0),H(1,12,12) , A1(32,0,0) ,
设 B1(0,0,t) ,则 A1E=(?12,0,1),EB1=(?1,0,t?1) ,由 A1E 与 EB1 共线得 A1E=λEB1 ,
得 {?12=?λ1=λ(t?1) ,解得 t=3 ,所以 B1(0,0,3) ,同理得 C1(0,3,0) ,
可得 A1B1=(?32,0,3),A1C1=(?32,3,0) ,设平面 A1B1C1 的一个法向量为 n=(x,y,z) ,
{?32x+3z=0?32x+3y=0 ?,令 x=2 ,得 y=z=1 ,即 n=(2,1,1) , OC1=(0,3,0) ,
设直线 OC1 与平面 A1B1C1 所成角为 θ ,则 sinθ=|cos?n,OC1?|=|n?OC1||n||OC1|=33×6=66 ,
则直线 OC1 与平面 A1B1C1 所成角的正弦值为 66
【解析】(1)根据题意证明 EF// 面 OBC ,由线面平行的性质定理得 EF//B1C1 ,由已知可得 EF⊥AH ,即得 B1C1⊥AH ,再证明 OA⊥ 面 OBC ,得 OA⊥ B1C1 ,由线面垂直的判定定理即可得到证明.(2)以直线 OA,OB,OC 分别为 x,y,z 轴建立空间直角坐标系,求 OC1 的坐标和平面 A1B1C1 的法向量,由线面角的向量公式进行计算即可得到答案.
