1.3空间向量及其运算的坐标表示-【新教材】人教A版(2019)高中数学选择性必修第一册课后练习(Word含答案)
文档属性
| 名称 | 1.3空间向量及其运算的坐标表示-【新教材】人教A版(2019)高中数学选择性必修第一册课后练习(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 236.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 00:00:00 | ||
图片预览



文档简介
1.3空间向量及其运算的坐标表示
一、单选题
1.已如向量false,false,且false与false互相垂直,则false( ).
A.false B.false C.false D.false
2.向量false,若false,且false,则false的值为( )
A.false B.1 C.3或1 D.false或1
3.已知平面false的法向量为false,若直线false平面false,则直线l的方向向量可以为( )
A.false B.false
C.false D.false
4.已知false,false,则false的最小值为( )
A.false B.false C.false D.false
5.已知长方体false,正方形false所在平面记为false,若经过点false的直线false与长方体false所有的棱所成角相等,且false,则线段false的长为( )
A.false B.false C.false D.false
6.在空间直角坐标系中,点false关于平面false的对称点为false,则false( )
A.false B.false C.false D.false
7.如图,在空间直角坐标系中,正方体ABCD-A1B1C1D1的棱长为1,B1E1=falseA1B1,则false等于( )
A.false B.false C.false D.false
8.在棱长均为false的四面体false中,点false为false的中点,点false为false的中点.若点false,false是平面false内的两动点,且false,false,则false的面积为( )
A.false B.3
C.false D.2
二、填空题
9.已知false,false,则false _____.
10.已知空间三点false,若false,且false分别与false垂直,则向量false__________.
11.已知长方体false,false,false,在false上取一点M,在false上取一点N,使得直线false平面false,则线段MN的最小值为________.
12.已知直线false与平面false垂直,直线false的一个方向向量为false,向量false与平面false平行,则false______.
三、解答题
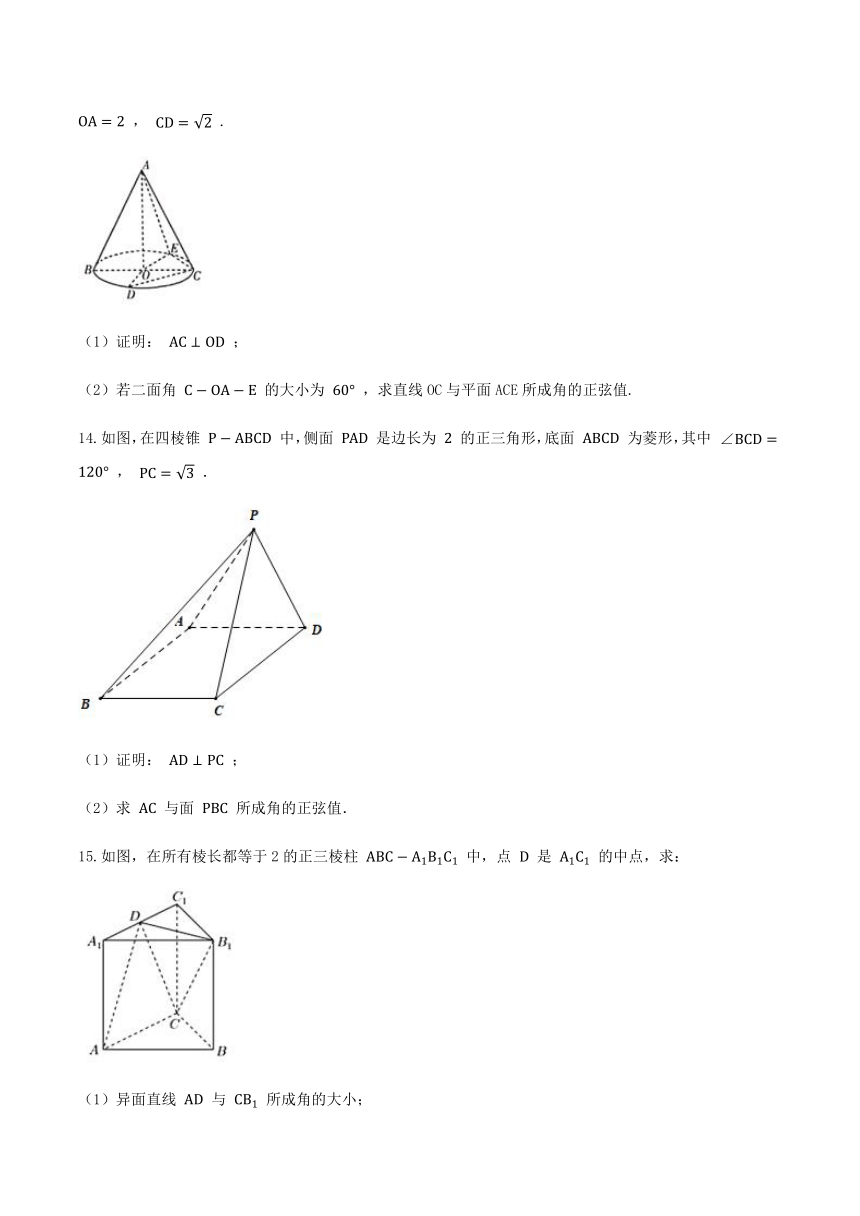
13.如图所示,圆锥的顶点为A,底面的圆心为O,BC是底面圆的一条直径,点D,E在底面圆上,已知 BC=OA=2 , CD=2 .
(1)证明: AC⊥OD ;
(2)若二面角 C?OA?E 的大小为 60° ,求直线OC与平面ACE所成角的正弦值.
14.如图,在四棱锥 P?ABCD 中,侧面 PAD 是边长为 2 的正三角形,底面 ABCD 为菱形,其中 ∠BCD=120° , PC=3 .
(1)证明: AD⊥PC ;
(2)求 AC 与面 PBC 所成角的正弦值.
15.如图,在所有棱长都等于2的正三棱柱 ABC?A1B1C1 中,点 D 是 A1C1 的中点,求:
(1)异面直线 AD 与 CB1 所成角的大小;
(2)直线 B1B 与平面 B1DC 所成角的大小.
16.如图,在四棱锥 S?ABCD 中,二面角 S?AD?B 的大小为90°, AB//CD , ∠DCB=1350 , AB=CD=DS=2AD=2AS=22 , DE=EC,SF=λSB(0<λ<1) .
(1)求证: AD⊥SC ;
(2)试确定 λ 的值,使得直线 EF 与平面 SDC 所成的角的正弦值为 |?2λ+2|12λ2?8λ+6 .
参考答案
B2.D3.B4.A5.D6.D7.C8.C9.false10.false或false11.false12.3
13.【答案】 (1)证明:因为 OC=OD , CD=2 ,所以 DC2=OC2+OD2 ,
所以 OD⊥OC .
在圆锥AO中,AO与底面垂直,
所以 AO⊥OD .
因为 AO∩OC=O ,
所以 OD⊥ 平面OAC,
因为 AC? 平面OAC,
所以 AC⊥OD .
(2)解:由(1)可知0A,OC,OD两两垂直,以O为原点建立如图所示的空间直角坐标系.
则 O(0,0,0) , C(0,1,0) , A(0,0,2) .
因为 AO⊥OC , AO⊥OE ,所以 ∠COE 为二面角 C?OA?E 的平面角,
所以 ∠COE=60° ,从而可得 E(?32,12,0) .
所以 AC=(0,1,?2) , CE=(?32,?12,0) , OC=(0,1,0) .
设平面ACE的法向量为 n=(x,y,z) .
则 {AC?n=y?2z=0CE?n=?32x?12y=0 .令 z=1 ,则 n=(?233,2,1) .
设直线OC与平面ACE所成的角为 θ ,
则 sinθ=|cos?OC,n?|=|OC?n||OC||n|=243+4+1=25719 .
【解析】(1)由 DC2=OC2+OD2 可得 OD⊥OC ,易证 OD⊥ 平面OAC,即可求得 AC⊥OD (2)建立空间直角坐标系,利用线面角计算公式求解即可.
14.【答案】 (1)证明:取 AD 中点 E ,则 PE⊥AD
OE⊥AD ,则 AD⊥ 平面 PEC ,因此 AD⊥PC
(2)解:方法一:由题意可得 ΔPOC 为正三角形
且平面 PEC⊥ 平面 ABCD ,则取 CE 中点 O ,因此 PO⊥ 平面 ABCD .
PO=PC×sin60°=32 , SΔPBC=12BC×PC=3 , SΔABC=3
由等体积法可得 VA?PBC=VP?ABC ,即 13SΔPBC×hA=13SΔABC×OP ,则 hA=PO=32
因此 AC 与面 PBC 所成角的正弦值为 hAAC=34 .
方法二:设 AC 与面 PBC 所成角为 θ , sinθ=dA→面PBCAC=dE→面PBCAC=32×32=34 .
方法三:如图建立空间直角坐标系 O?xyz ;
则 P(0,0,32) , A(?32,?1,0) , C(32,0,0) B(32,?2,0) ,则 BC=(0,?2,0) , PC=(32,0,?32) , AC=(3,1,0) .
设平面 PBC 的法向量为 n=(x,y,z) ,则 {PC?n=32x?32z=0BC?n=?2y=0 ,
令 x=3 ,
则 n=(3,0,1)
则 AC 与面 PBC 所成角的正弦值为 |AC?n|AC|?|n||=34
【解析】(1)取 AD 中点 E ,则 PE⊥AD , OE⊥AD ,从而 AD⊥ 平面 PEC ,由此能证明 AD⊥PC .(2)取 CE 中点 O ,则 PO⊥ 平面 ABCD ,由等体积法可得 VA?PBC=VP?ABC ,求出 hA=PO=32 , AC 与面 PBC 所成角 θ 的正弦值为: sinθ=hAAC ,由此能求出结果.
15.【答案】 (1)解:取 AC 中点 E ,连接 DE ,则 DE//AA1 ,
正三棱柱 ABC?A1B1C1 所有棱长都等于2,
BE⊥AC , AA1⊥ 平面 ABC,∴DE⊥ 平面 ABC ,
以 E 为坐标原点, EA,EB,ED 所在的直线分别为
x,y,z 轴建立空间直角坐标系,则 A(1,0,0),D(0,0,2) ,
C(?1,0,0),B(0,3,0),B1(0,3,2) .
AD=(?1,0,2),CB1=(1,3,2)
cosAD,CB1=AD?CB1|AD||CB1|=3320
∴ 异面直线 AD 与 CB1 所成角的余弦为 3320 .
∴ 异面直线 AD 与 CB1 所成角是 arccos3320 .
(2)解: B1B=(0,0,2),DB1=(0,3,0),DC=(?1,0?2) ,
设平面 B1DC 的法向量 n=(x,y,z),n⊥DB1,n⊥DC ,
{n?DB1=3y=0n?DC=?x?2y=0 , y=0 ,令 y=?1 ,则 x=2 ,
∴ 平面 B1DC 的一个法向量 n=(2,0,?1),
设直线 B1B 与平面 B1DC 所成角 α ,
sinα=|cosB1B,n|=|B1B?n||B1B||n|=22×5=55 ,
∴ 直线 B1B 与平面 B1DC 所成角 arcsin55 .
【解析】(1)建立空间直角坐标系,确定 AD,CB1 坐标,即可求出 AD,CB1 所成角的余弦,转化为 AD 与 CB1 所成角,即可求出结果;(2)确定 B1B 坐标,求出平面 B1DC 的法向量,利用线面角公式,即可求出直线 B1B 与平面 B1DC 所成角
16.【答案】 (1)证明 :因为 AB//CD ,且 AB=CD ,故四边形 ABCD 为平行四边形;
连接 AC ,
因为 AB=22,BC=2,∠DCB=1350,∠ABC=450 ,
由余弦定理得 AC2=8+4?2?22?2?cos450=4 ,
得 AC=2 ,所以 ∠ACB=900 ,即 BC⊥AC ,又 AD//BC ,
所以 AD⊥AC ,又 AD=AS=2,DS=22 ,所以 SA⊥AD,AS∩AC=A ,所以
AD⊥ 平面 SAC ,所以 AD⊥SC
(2)解:因为二面角 S?AD?B 的大小为90°, SA⊥AD ,所以 SA⊥ 底面 ABCD ,所以直线 AC,AD,AS 两两互相垂直,以 A 为原点,直线 AD,AC,AS 坐标轴,建立如图所示空间直角坐标系 A?xyz ,则 A(0,0,0),D(?2,0,0),C(0,2,0),B(2,2,0),E(?1,1,0),S(0,0,2) ,所以 SC=(0,2,?2),SD=(?2,0,?2),SB=(2,2,?2) ,则 SF=(2λ,2λ,?2λ),F(2λ,2λ,?2λ+2) ,
所以 EF=(2λ+1,2λ?1,?2λ+2) ,设平面 SDC 的法向量为 n=(x,y,z) ,由 n·SC=0,n·SD=0 ,
得 {2y?2z=0?2x?2z=0 ,令 x=1 ,得 n=(1,?1,?1) .
依题意, |EF·n||EF|·|n|=|?2λ+2|12λ2?8λ+6 ,化简可得 |2λ3|=|?2λ+2| ,
即 3|λ?1|=|λ| ,解得 λ=3?32
【解析】(1)先证明AD垂直于平面SAC中两条相交直线AC,SA,即得到A D ⊥ 平面 S A C,从而A D ⊥ S C;
(2)建立空间直角坐标系 A ? x y z ,写出各点的坐标,得到向量EF的坐标,求出平面 SDC的法向量的坐标,由向量的数量积为0,求出λ的值.
一、单选题
1.已如向量false,false,且false与false互相垂直,则false( ).
A.false B.false C.false D.false
2.向量false,若false,且false,则false的值为( )
A.false B.1 C.3或1 D.false或1
3.已知平面false的法向量为false,若直线false平面false,则直线l的方向向量可以为( )
A.false B.false
C.false D.false
4.已知false,false,则false的最小值为( )
A.false B.false C.false D.false
5.已知长方体false,正方形false所在平面记为false,若经过点false的直线false与长方体false所有的棱所成角相等,且false,则线段false的长为( )
A.false B.false C.false D.false
6.在空间直角坐标系中,点false关于平面false的对称点为false,则false( )
A.false B.false C.false D.false
7.如图,在空间直角坐标系中,正方体ABCD-A1B1C1D1的棱长为1,B1E1=falseA1B1,则false等于( )
A.false B.false C.false D.false
8.在棱长均为false的四面体false中,点false为false的中点,点false为false的中点.若点false,false是平面false内的两动点,且false,false,则false的面积为( )
A.false B.3
C.false D.2
二、填空题
9.已知false,false,则false _____.
10.已知空间三点false,若false,且false分别与false垂直,则向量false__________.
11.已知长方体false,false,false,在false上取一点M,在false上取一点N,使得直线false平面false,则线段MN的最小值为________.
12.已知直线false与平面false垂直,直线false的一个方向向量为false,向量false与平面false平行,则false______.
三、解答题
13.如图所示,圆锥的顶点为A,底面的圆心为O,BC是底面圆的一条直径,点D,E在底面圆上,已知 BC=OA=2 , CD=2 .
(1)证明: AC⊥OD ;
(2)若二面角 C?OA?E 的大小为 60° ,求直线OC与平面ACE所成角的正弦值.
14.如图,在四棱锥 P?ABCD 中,侧面 PAD 是边长为 2 的正三角形,底面 ABCD 为菱形,其中 ∠BCD=120° , PC=3 .
(1)证明: AD⊥PC ;
(2)求 AC 与面 PBC 所成角的正弦值.
15.如图,在所有棱长都等于2的正三棱柱 ABC?A1B1C1 中,点 D 是 A1C1 的中点,求:
(1)异面直线 AD 与 CB1 所成角的大小;
(2)直线 B1B 与平面 B1DC 所成角的大小.
16.如图,在四棱锥 S?ABCD 中,二面角 S?AD?B 的大小为90°, AB//CD , ∠DCB=1350 , AB=CD=DS=2AD=2AS=22 , DE=EC,SF=λSB(0<λ<1) .
(1)求证: AD⊥SC ;
(2)试确定 λ 的值,使得直线 EF 与平面 SDC 所成的角的正弦值为 |?2λ+2|12λ2?8λ+6 .
参考答案
B2.D3.B4.A5.D6.D7.C8.C9.false10.false或false11.false12.3
13.【答案】 (1)证明:因为 OC=OD , CD=2 ,所以 DC2=OC2+OD2 ,
所以 OD⊥OC .
在圆锥AO中,AO与底面垂直,
所以 AO⊥OD .
因为 AO∩OC=O ,
所以 OD⊥ 平面OAC,
因为 AC? 平面OAC,
所以 AC⊥OD .
(2)解:由(1)可知0A,OC,OD两两垂直,以O为原点建立如图所示的空间直角坐标系.
则 O(0,0,0) , C(0,1,0) , A(0,0,2) .
因为 AO⊥OC , AO⊥OE ,所以 ∠COE 为二面角 C?OA?E 的平面角,
所以 ∠COE=60° ,从而可得 E(?32,12,0) .
所以 AC=(0,1,?2) , CE=(?32,?12,0) , OC=(0,1,0) .
设平面ACE的法向量为 n=(x,y,z) .
则 {AC?n=y?2z=0CE?n=?32x?12y=0 .令 z=1 ,则 n=(?233,2,1) .
设直线OC与平面ACE所成的角为 θ ,
则 sinθ=|cos?OC,n?|=|OC?n||OC||n|=243+4+1=25719 .
【解析】(1)由 DC2=OC2+OD2 可得 OD⊥OC ,易证 OD⊥ 平面OAC,即可求得 AC⊥OD (2)建立空间直角坐标系,利用线面角计算公式求解即可.
14.【答案】 (1)证明:取 AD 中点 E ,则 PE⊥AD
OE⊥AD ,则 AD⊥ 平面 PEC ,因此 AD⊥PC
(2)解:方法一:由题意可得 ΔPOC 为正三角形
且平面 PEC⊥ 平面 ABCD ,则取 CE 中点 O ,因此 PO⊥ 平面 ABCD .
PO=PC×sin60°=32 , SΔPBC=12BC×PC=3 , SΔABC=3
由等体积法可得 VA?PBC=VP?ABC ,即 13SΔPBC×hA=13SΔABC×OP ,则 hA=PO=32
因此 AC 与面 PBC 所成角的正弦值为 hAAC=34 .
方法二:设 AC 与面 PBC 所成角为 θ , sinθ=dA→面PBCAC=dE→面PBCAC=32×32=34 .
方法三:如图建立空间直角坐标系 O?xyz ;
则 P(0,0,32) , A(?32,?1,0) , C(32,0,0) B(32,?2,0) ,则 BC=(0,?2,0) , PC=(32,0,?32) , AC=(3,1,0) .
设平面 PBC 的法向量为 n=(x,y,z) ,则 {PC?n=32x?32z=0BC?n=?2y=0 ,
令 x=3 ,
则 n=(3,0,1)
则 AC 与面 PBC 所成角的正弦值为 |AC?n|AC|?|n||=34
【解析】(1)取 AD 中点 E ,则 PE⊥AD , OE⊥AD ,从而 AD⊥ 平面 PEC ,由此能证明 AD⊥PC .(2)取 CE 中点 O ,则 PO⊥ 平面 ABCD ,由等体积法可得 VA?PBC=VP?ABC ,求出 hA=PO=32 , AC 与面 PBC 所成角 θ 的正弦值为: sinθ=hAAC ,由此能求出结果.
15.【答案】 (1)解:取 AC 中点 E ,连接 DE ,则 DE//AA1 ,
正三棱柱 ABC?A1B1C1 所有棱长都等于2,
BE⊥AC , AA1⊥ 平面 ABC,∴DE⊥ 平面 ABC ,
以 E 为坐标原点, EA,EB,ED 所在的直线分别为
x,y,z 轴建立空间直角坐标系,则 A(1,0,0),D(0,0,2) ,
C(?1,0,0),B(0,3,0),B1(0,3,2) .
AD=(?1,0,2),CB1=(1,3,2)
cosAD,CB1=AD?CB1|AD||CB1|=3320
∴ 异面直线 AD 与 CB1 所成角的余弦为 3320 .
∴ 异面直线 AD 与 CB1 所成角是 arccos3320 .
(2)解: B1B=(0,0,2),DB1=(0,3,0),DC=(?1,0?2) ,
设平面 B1DC 的法向量 n=(x,y,z),n⊥DB1,n⊥DC ,
{n?DB1=3y=0n?DC=?x?2y=0 , y=0 ,令 y=?1 ,则 x=2 ,
∴ 平面 B1DC 的一个法向量 n=(2,0,?1),
设直线 B1B 与平面 B1DC 所成角 α ,
sinα=|cosB1B,n|=|B1B?n||B1B||n|=22×5=55 ,
∴ 直线 B1B 与平面 B1DC 所成角 arcsin55 .
【解析】(1)建立空间直角坐标系,确定 AD,CB1 坐标,即可求出 AD,CB1 所成角的余弦,转化为 AD 与 CB1 所成角,即可求出结果;(2)确定 B1B 坐标,求出平面 B1DC 的法向量,利用线面角公式,即可求出直线 B1B 与平面 B1DC 所成角
16.【答案】 (1)证明 :因为 AB//CD ,且 AB=CD ,故四边形 ABCD 为平行四边形;
连接 AC ,
因为 AB=22,BC=2,∠DCB=1350,∠ABC=450 ,
由余弦定理得 AC2=8+4?2?22?2?cos450=4 ,
得 AC=2 ,所以 ∠ACB=900 ,即 BC⊥AC ,又 AD//BC ,
所以 AD⊥AC ,又 AD=AS=2,DS=22 ,所以 SA⊥AD,AS∩AC=A ,所以
AD⊥ 平面 SAC ,所以 AD⊥SC
(2)解:因为二面角 S?AD?B 的大小为90°, SA⊥AD ,所以 SA⊥ 底面 ABCD ,所以直线 AC,AD,AS 两两互相垂直,以 A 为原点,直线 AD,AC,AS 坐标轴,建立如图所示空间直角坐标系 A?xyz ,则 A(0,0,0),D(?2,0,0),C(0,2,0),B(2,2,0),E(?1,1,0),S(0,0,2) ,所以 SC=(0,2,?2),SD=(?2,0,?2),SB=(2,2,?2) ,则 SF=(2λ,2λ,?2λ),F(2λ,2λ,?2λ+2) ,
所以 EF=(2λ+1,2λ?1,?2λ+2) ,设平面 SDC 的法向量为 n=(x,y,z) ,由 n·SC=0,n·SD=0 ,
得 {2y?2z=0?2x?2z=0 ,令 x=1 ,得 n=(1,?1,?1) .
依题意, |EF·n||EF|·|n|=|?2λ+2|12λ2?8λ+6 ,化简可得 |2λ3|=|?2λ+2| ,
即 3|λ?1|=|λ| ,解得 λ=3?32
【解析】(1)先证明AD垂直于平面SAC中两条相交直线AC,SA,即得到A D ⊥ 平面 S A C,从而A D ⊥ S C;
(2)建立空间直角坐标系 A ? x y z ,写出各点的坐标,得到向量EF的坐标,求出平面 SDC的法向量的坐标,由向量的数量积为0,求出λ的值.
