圆周角课件

(共25张PPT)
24.1圆周角
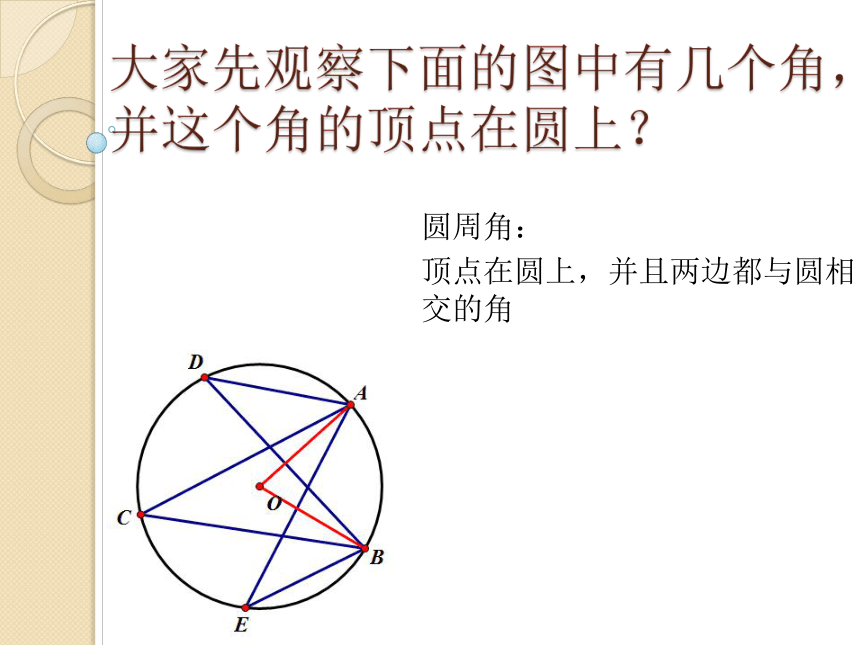
大家先观察下面的图中有几个角，并这个角的顶点在圆上？
圆周角：
顶点在圆上，并且两边都与圆相交的角


√
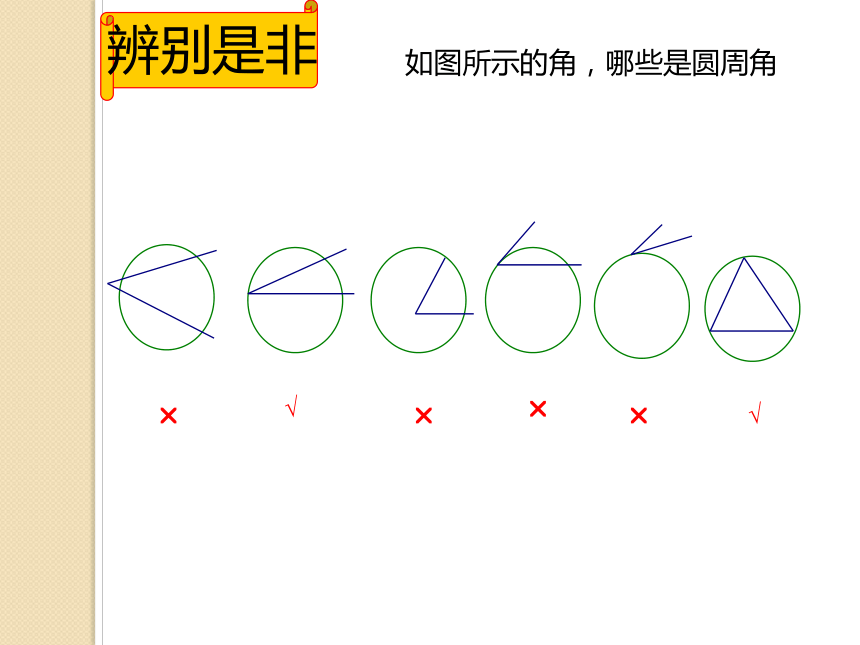
辨别是非
如图所示的角，哪些是圆周角


√
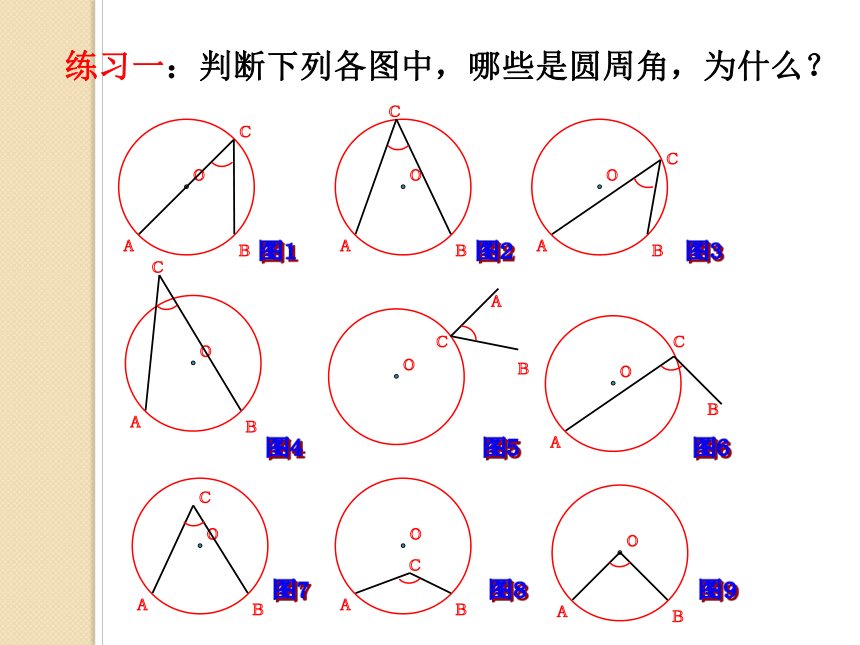
练习一：判断下列各图中，哪些是圆周角，为什么？
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
C
C
C
C
C
C
C
C
图1
图2
图3
图4
图5
图6
图7
图8
图9
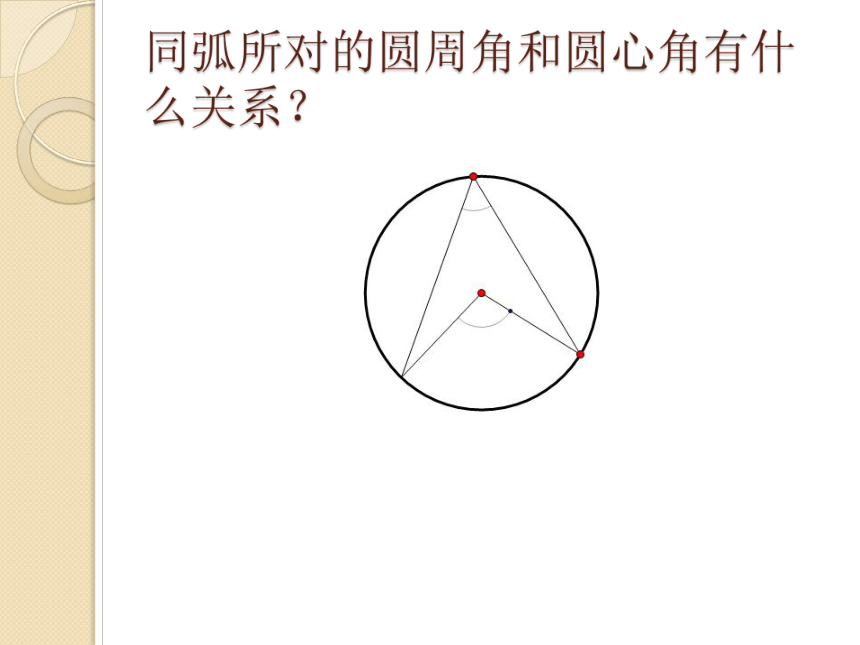
同弧所对的圆周角和圆心角有什么关系？
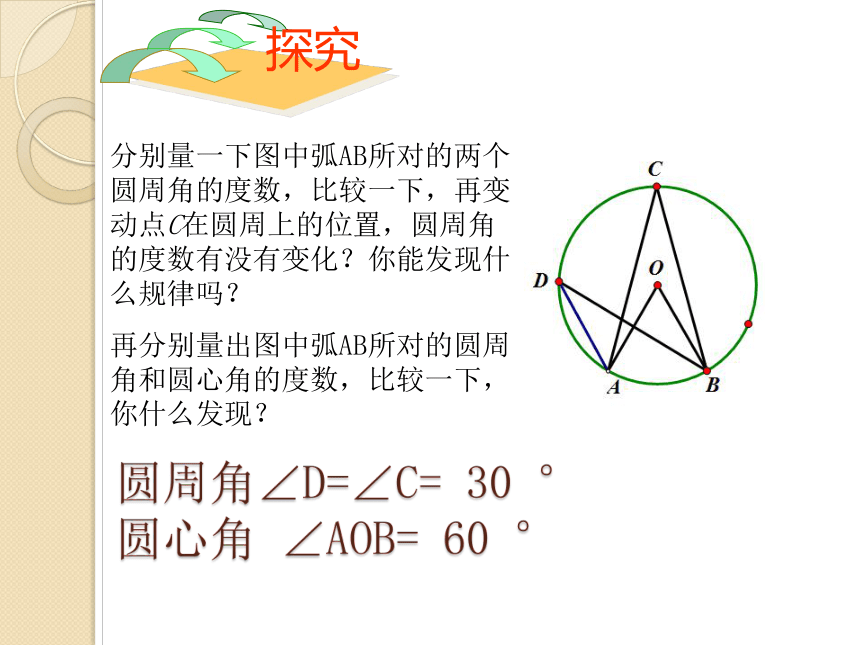
探究
分别量一下图中弧AB所对的两个圆周角的度数，比较一下，再变动点C在圆周上的位置，圆周角的度数有没有变化？你能发现什么规律吗？
再分别量出图中弧AB所对的圆周角和圆心角的度数，比较一下，你什么发现？
圆周角∠D=∠C= 30 °
圆心角 ∠AOB= 60 °
发现：同弧所对的圆周角的度数没有变化，并且它的度数恰好等于这条弧所对的圆心角的度数的一半．
猜想：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．相等的圆周角所对的弧也相等。
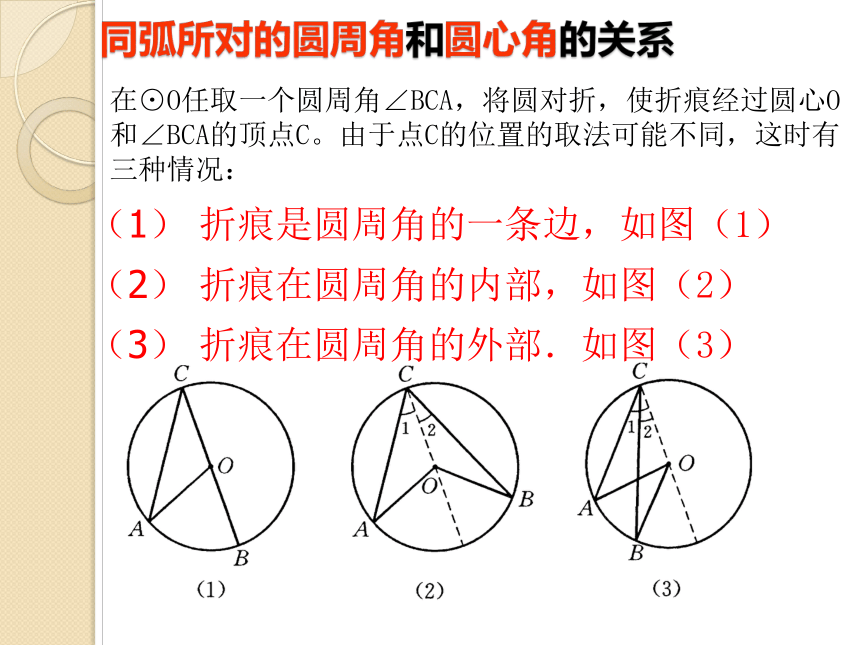
同弧所对的圆周角和圆心角的关系
在⊙O任取一个圆周角∠BCA，将圆对折，使折痕经过圆心O和∠BCA的顶点C。由于点C的位置的取法可能不同，这时有三种情况：
（1） 折痕是圆周角的一条边，如图（1）
（2） 折痕在圆周角的内部，如图（2）
（3） 折痕在圆周角的外部．如图（3）
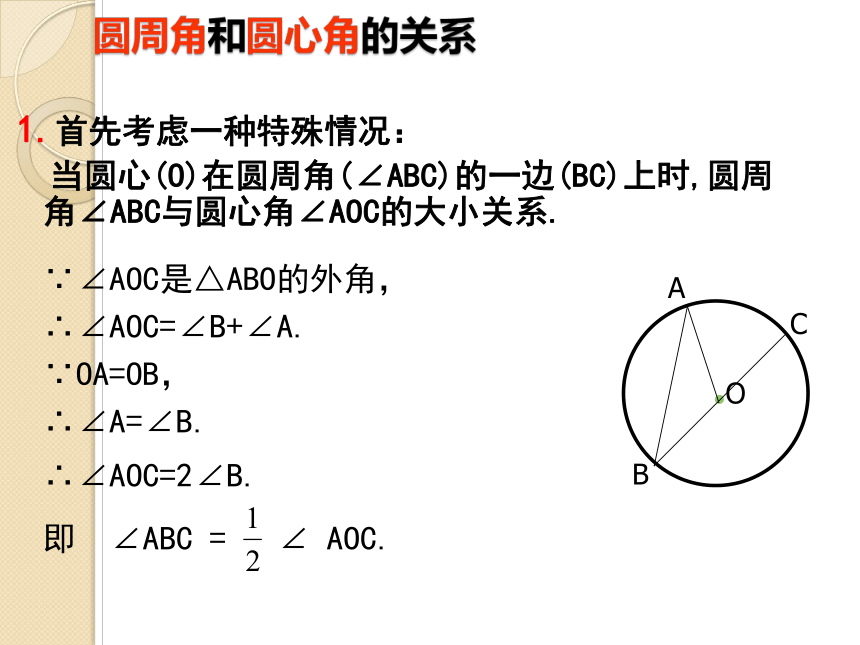
圆周角和圆心角的关系
1.首先考虑一种特殊情况：
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
∵∠AOC是△ABO的外角，
∴∠AOC=∠B+∠A.
∵OA=OB，
●O
A
B
C
∴∠A=∠B.
∴∠AOC=2∠B.
即 ∠ABC = ∠ AOC.
圆周角和圆心角的关系
2.考虑第二种情况
当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样
能否转化为1的情况
过点B作直径BD.由1可得:
●O
∴ ∠ABC = ∠AOC.
A
B
C
D
∠ABD = ∠AOD,
∠CBD = ∠COD,
圆周角和圆心角的关系
3.考虑第二种情况
当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样
能否也转化为1的情况
过点B作直径BD.由1可得:
●O
D
∠ABD = ∠AOD,∠CBD = ∠COD,
A
B
C
∴ ∠ABC = ∠AOC.
结 论：猜想正确
在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．相等的圆周角所对的弧也相等。
圆周角定理
推论：在同圆或等圆中，如果两个圆周角相等，它们所对的弧一定相等
巩固练习
如图，点A,B,C,D在同一个圆上，四边形ABCD的对角线把4个内角分成8个角，这些角中哪些是相等的角？
∠1=∠4，∠2=∠7
∠3=∠6，∠5=∠8
方法点拔：由同弧来找相等的圆周角
如图，⊙O中，弧AB=弧AC， ∠C=75 °，求∠A的度数
解： ∵弧AB=弧AC
由圆周角定理
∴ ∠B= ∠C
在△ABC中， ∠A, ∠B, ∠C是内角，
∴ ∠ A+∠B+ ∠C=180 °
又∵ ∠C=75 °
∴ ∠ A=∠B=52.5 °
思
考
如图，线段AB是⊙O的直径，点C是⊙O上任意一点（除点A、B），那么，∠ACB就是直径AB所对的圆周角，想想看，∠ACB会是怎样的角？
O
C
B
A
90°的圆周角所对的弦是什么
证明：AB是圆O的直径，C是圆上一点
连接OC，那么OC=OA=OB
所以，∠A=∠ACO，∠BCO=∠B
因为∠A+∠B+∠ACB=180
所以，∠A+∠B+∠ACO+∠BCO=180
由此可得，2(∠ACO+∠BCO_)=2∠ABC=180
所以，∠ACB=90
即直径所对的圆周角是直角
三角形ABC是圆O的内接三角形。∠ACB=90
设点O是斜边AB上的中点。连接OC
因为直角三角形斜边上的中线等于斜边的一半
所以，OC=OA=OB
点O到圆上三点的距离相等，三个点确定一个圆，
所以，O是圆心，所以AB是圆O的直径
即90度圆周角所对的弦是直径
∠ACB会是怎样的角？
90°的圆周角所对的弦是什么
·
A
B
C1
O
C2
C3
半圆（或直径）所对的圆周角是直角， 90°的圆周角所对的弦是直径．
推 论
巩固小练
如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到C，使AC=AB，BD与CD的大小有什么关系？为什么？
解：BD=CD
理由是：如图24-30连接AD
∵AB是⊙O的直径
∴∠ADB=90°即AD⊥BC
又∵AC=AB
∴BD=CD
分析：BD=CD，因为AB=AC，所以这个△ABC是等腰，要证明D是BC的中点，只要连结AD证明AD是高或是∠BAC的平分线即可．
圆内接多边形
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形。
这个圆叫做这个多边形的外接圆
∴∠A+∠BCD=180°
同理,∠ABC+∠ADC=180°
∵ 与 所对的
圆心角的和是360°
当圆内接四边形时四边形的内角有什么关系？
∵ ∠A所对弧为 ， ∠C所对弧为
根据以上证明你能得到什么结论？
圆内接四边形的性质
圆内接四边形的对角互补
如图，⊙0的直径AB为10㎝，弦AC为6㎝， ∠ACB的平分线交⊙O于D，求BC,AD,BD的长
例题2
解： ∵AB是直径
∴ ∠ ACB= ∠ ADB=90
在Rt △ ABC中，
BC= =8
∵CD平分∠ACB,
∴AD=BD
又在Rt △ ABD中，
1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
2.在同圆(或等圆)中，同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半；相等的圆周角所对的弧相等。
3.半圆或直径所对的圆周角都相等，都等于90°
90°的圆周角所对的弦是圆的直径
我的收获
概念的引入和定理的发现：
定义：顶点在圆上，两边都和圆相交的角叫做圆周角。
定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，
都等于该弧所对的圆心角的一半。
这节课你有哪些收获？
我的收获
我们根据圆周角相对于圆心的位置把圆周角分成三类，先解决一类特殊问题，再把其他两类转化成特殊问题。
2、定理的证明思路：