人教版数学九下 28.1 锐角的余弦和正切 课件(20张)
文档属性
| 名称 | 人教版数学九下 28.1 锐角的余弦和正切 课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 924.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 00:00:00 | ||
图片预览



文档简介
BY YUSHEN
锐角的余弦和正切
TOPIC 28.1 ACUTE TRIANGLE (SINE, COSINE, TANGENT VALUE OF SPECIAL ANGLE)
第二十八章 锐角三角函数
BY YUSHEN
目录
CONTENTS
学习目标
1、理解余弦的概念。
2、理解正切的概念。
3、利用余弦、正切进行相关计算。
01
重点
理解余弦、正切的概念。
02
难点
利用余弦、正切进行相关计算。
03
BY YUSHEN
1
PART TWO
1、理解余弦的概念。
2、理解正切的概念。
3、利用余弦、正切进行相关计算。
学习目标
LEARNING OBJECTIVES
BY YUSHEN
探究与思考
01
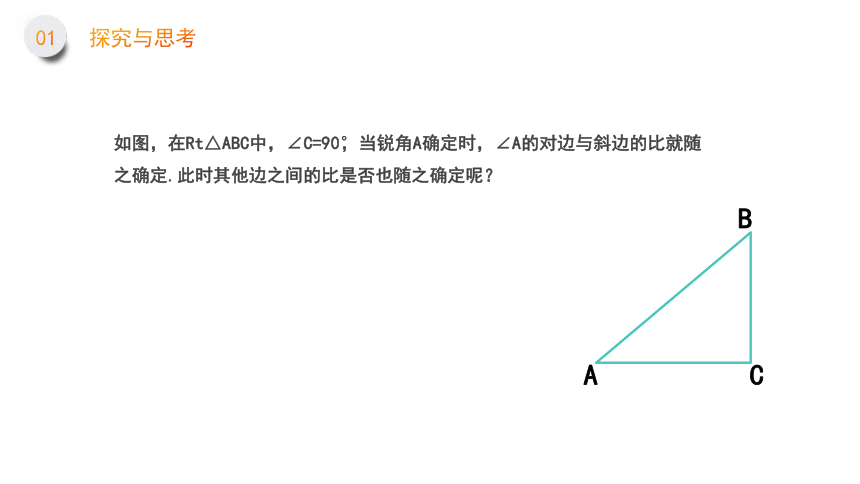
如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定.此时其他边之间的比是否也随之确定呢?
A
B
C
BY YUSHEN
探索与思考
01
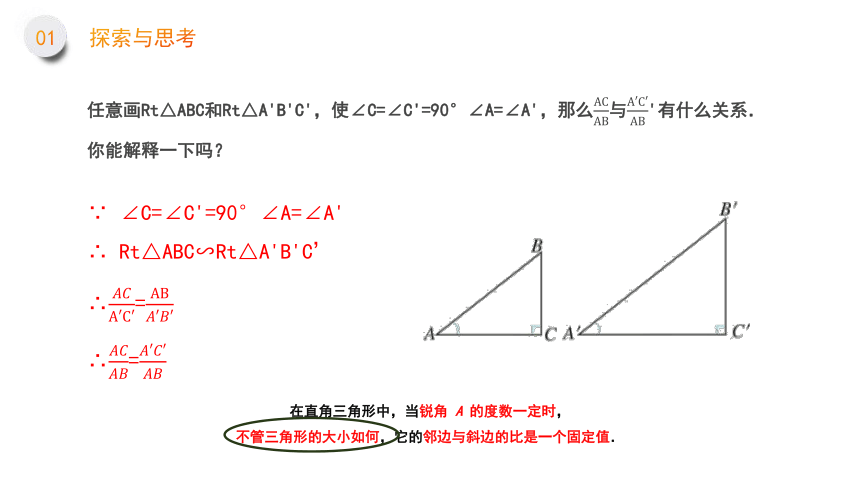
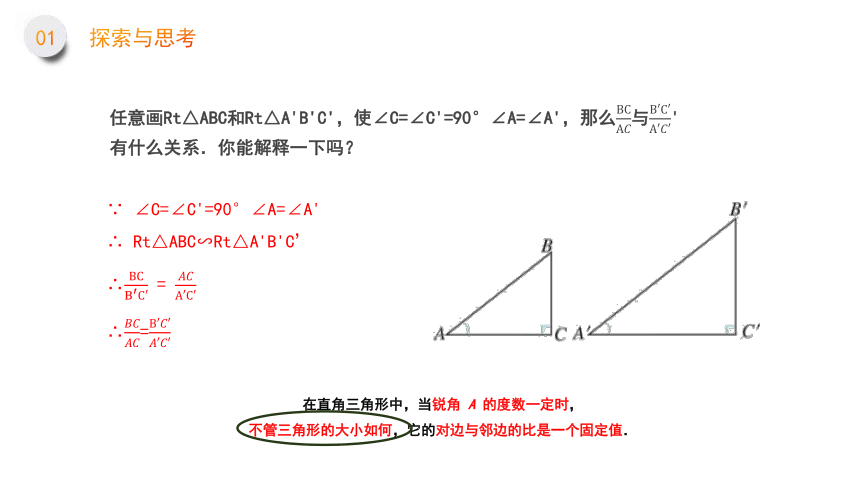
任意画Rt△ABC和Rt△A'B'C',使∠C=∠C'=90°∠A=∠A',那么ACAB与A′C′AB'有什么关系.
你能解释一下吗?
?
∵ ∠C=∠C'=90°∠A=∠A'
∴ Rt△ABC∽Rt△A'B'C’
∴????????A′C′=AB????′????′
∴????????????????=????′????′????????
?
在直角三角形中,当锐角 A 的度数一定时,
不管三角形的大小如何,它的邻边与斜边的比是一个固定值.
BY YUSHEN
余弦
01
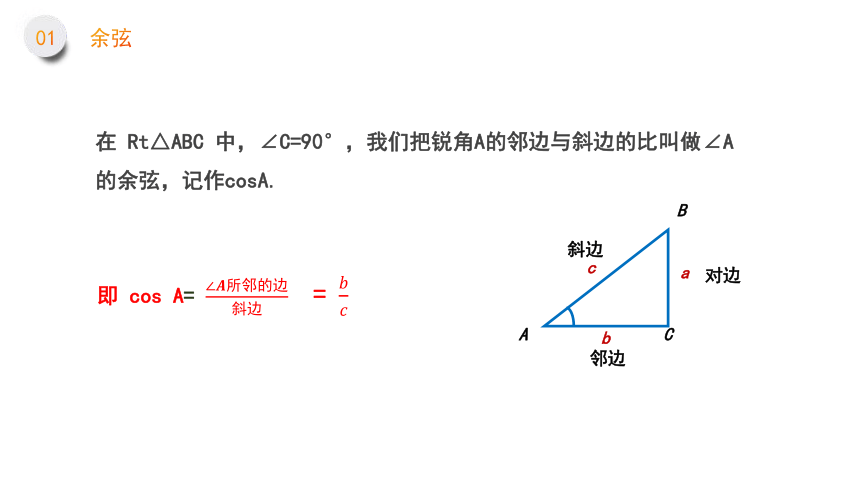
在 Rt△ABC 中,∠C=90°,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA.
即 cos A= ∠????所邻的边斜边 = ????????
?
对边
A
B
C
c
a
b
斜边
邻边
BY YUSHEN
正弦和余弦注意事项
01
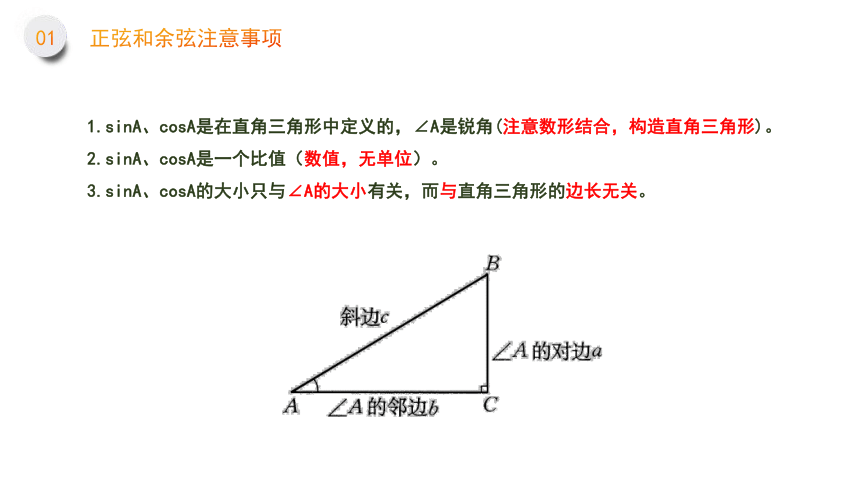
1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2.sinA、cosA是一个比值(数值,无单位)。
3.sinA、cosA的大小只与∠A的大小有关,而与直角三角形的边长无关。
BY YUSHEN
探索与思考
01
任意画Rt△ABC和Rt△A'B'C',使∠C=∠C'=90°∠A=∠A',那么BCA????与B′C′A′????′'有什么关系.你能解释一下吗?
?
∵ ∠C=∠C'=90°∠A=∠A'
∴ Rt△ABC∽Rt△A'B'C’
∴BCB′C′ = ????????A′C′
∴????????????????=B′????′????′????′
?
在直角三角形中,当锐角 A 的度数一定时,
不管三角形的大小如何,它的对边与邻边的比是一个固定值.
BY YUSHEN
正切
01
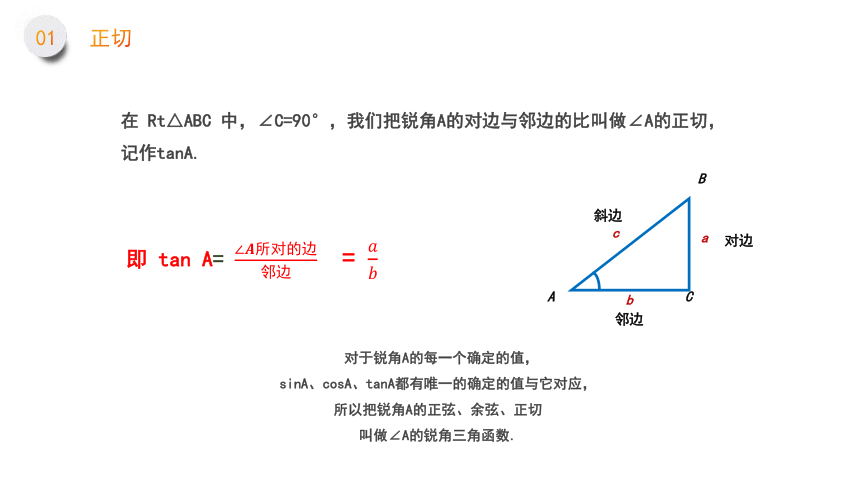
在 Rt△ABC 中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的正切,记作tanA.
即 tan A= ∠????所对的边邻边 = ????????
?
对边
A
B
C
c
a
b
斜边
邻边
对于锐角A的每一个确定的值,
sinA、cosA、tanA都有唯一的确定的值与它对应,
所以把锐角A的正弦、余弦、正切
叫做∠A的锐角三角函数.
2
BY YUSHEN
PART TWO
1、理解余弦的概念。
2、理解正切的概念。
3、利用余弦、正切进行相关计算。
练一练
HOMEWORK PRACTICE
BY YUSHEN
练一练
02
在 Rt△ABC 中,∠C=90°,若∠A=30°且 BC=2,求cosA=?
A
B
C
∵ ∠C=90°,∠A=30°
而在Rt△ABC中, 30°角所对的边等于斜边的一边
∴AB=4, 由勾股定理得AC= ????????????????????????? =2????
∴cos A= ????????????????= 2????????= ????????
?
BY YUSHEN
练一练
02
在 Rt△ABC 中,∠C=90°,若∠A=45°且 BC=2,求cosA=?
A
B
C
∵ ∠C=90°,∠A=45°
∴ Rt△ABC为等腰直角三角形,BC=AC=2
由勾股定理得AB= ????????????+???????????? =2????
∴cos A= ????????????????= 22????= ????????
?
若∠A=60°且AC=2,求cosA=?
BY YUSHEN
练一练
02
在 Rt△ABC 中,∠C=90°,若∠A=30°且 BC=2,求tanA=?
A
B
C
∵ ∠C=90°,∠A=30°
而在Rt△ABC中, 30°角所对的边等于斜边的一边
∴AB=4, 由勾股定理得AC= ????????????????????????? =2????
∴tanA= ????????????????= ????2????= ????????
?
BY YUSHEN
练一练
02
在 Rt△ABC 中,∠C=90°,若∠A=45°且 BC=2,求tanA=?
A
B
C
∵ ∠C=90°,∠A=45°
∴ Rt△ABC为等腰直角三角形,BC=AC=2
∴ tanA= ?????????????????= ????
?
若∠A=60°,求tanA=?
BY YUSHEN
练一练
02
在 Rt△ABC 中,∠C=90°,若AB=10,BC=6,求tanA,sinA,cosA的值?
A
B
C
由勾股定理得AC= ????????2?????????2 =8
因此sinA= ???????????????? = 35
cosA= ?????????????????= 45
tanA= ?????????????????= 34
?
BY YUSHEN
变式
02
在 Rt△ABC 中,∠C=90°,若sinA= 35 ,求tanA,cosA的值?
?
A
B
C
BY YUSHEN
练一练
02
1.在△ABC中∠C=90°,tanA=33,则cosB=_____.
?
【答案】12
【详解】
解:∵在Rt△ABC中,∠C=90°,tanA=33,
设a=3x,b=3x,则c=23x,
∴cosB=????????=12.
故答案为:12.
?
2.在????????????????????????中,∠????=90°,如果????????=6,????????????????=23,那么????????= ;
?
【答案】4
【解析】
因为在????????????????????????中,∠????=90°,所以????????????????=????????????????=23,
所以????????=23????????=23×6=4.
?
BY YUSHEN
练一练
02
3. Rt△ABC中,∠C=90°,cosA=35,AC=6cm,那么BC等于_____.
?
【答案】8cm
【详解】
在????????△????????????中,∵?????????????????=????????????????,
∴????????=????????????????????????=635=10????????,
则????????=????????2?????????2=102?62=8????????.
故答案为:8????????.
?
4.(2019·四川东辰国际学校中考模拟)如图,正方形网格中每个小正方形的边长都是1,若点A、B、C都在格点上,则tan∠BAC的值是_____.
解:连接CD,∵∠CAD=∠ACD=45°,
∴∠ADC=90°,
由勾股定理得:AD=CD=12+11=2,
∴tan∠BAC=22=1,
故答案为:1.
?
BY YUSHEN
课后回顾
理解余弦的概念
01
理解正切的概念
02
利用余弦、正切
进行相关计算
03
BY YUSHEN
谢谢观看!
TOPIC 28.1 ACUTE TRIANGLE (SINE, COSINE, TANGENT VALUE OF SPECIAL ANGLE)
锐角的余弦和正切
TOPIC 28.1 ACUTE TRIANGLE (SINE, COSINE, TANGENT VALUE OF SPECIAL ANGLE)
第二十八章 锐角三角函数
BY YUSHEN
目录
CONTENTS
学习目标
1、理解余弦的概念。
2、理解正切的概念。
3、利用余弦、正切进行相关计算。
01
重点
理解余弦、正切的概念。
02
难点
利用余弦、正切进行相关计算。
03
BY YUSHEN
1
PART TWO
1、理解余弦的概念。
2、理解正切的概念。
3、利用余弦、正切进行相关计算。
学习目标
LEARNING OBJECTIVES
BY YUSHEN
探究与思考
01
如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定.此时其他边之间的比是否也随之确定呢?
A
B
C
BY YUSHEN
探索与思考
01
任意画Rt△ABC和Rt△A'B'C',使∠C=∠C'=90°∠A=∠A',那么ACAB与A′C′AB'有什么关系.
你能解释一下吗?
?
∵ ∠C=∠C'=90°∠A=∠A'
∴ Rt△ABC∽Rt△A'B'C’
∴????????A′C′=AB????′????′
∴????????????????=????′????′????????
?
在直角三角形中,当锐角 A 的度数一定时,
不管三角形的大小如何,它的邻边与斜边的比是一个固定值.
BY YUSHEN
余弦
01
在 Rt△ABC 中,∠C=90°,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA.
即 cos A= ∠????所邻的边斜边 = ????????
?
对边
A
B
C
c
a
b
斜边
邻边
BY YUSHEN
正弦和余弦注意事项
01
1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2.sinA、cosA是一个比值(数值,无单位)。
3.sinA、cosA的大小只与∠A的大小有关,而与直角三角形的边长无关。
BY YUSHEN
探索与思考
01
任意画Rt△ABC和Rt△A'B'C',使∠C=∠C'=90°∠A=∠A',那么BCA????与B′C′A′????′'有什么关系.你能解释一下吗?
?
∵ ∠C=∠C'=90°∠A=∠A'
∴ Rt△ABC∽Rt△A'B'C’
∴BCB′C′ = ????????A′C′
∴????????????????=B′????′????′????′
?
在直角三角形中,当锐角 A 的度数一定时,
不管三角形的大小如何,它的对边与邻边的比是一个固定值.
BY YUSHEN
正切
01
在 Rt△ABC 中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的正切,记作tanA.
即 tan A= ∠????所对的边邻边 = ????????
?
对边
A
B
C
c
a
b
斜边
邻边
对于锐角A的每一个确定的值,
sinA、cosA、tanA都有唯一的确定的值与它对应,
所以把锐角A的正弦、余弦、正切
叫做∠A的锐角三角函数.
2
BY YUSHEN
PART TWO
1、理解余弦的概念。
2、理解正切的概念。
3、利用余弦、正切进行相关计算。
练一练
HOMEWORK PRACTICE
BY YUSHEN
练一练
02
在 Rt△ABC 中,∠C=90°,若∠A=30°且 BC=2,求cosA=?
A
B
C
∵ ∠C=90°,∠A=30°
而在Rt△ABC中, 30°角所对的边等于斜边的一边
∴AB=4, 由勾股定理得AC= ????????????????????????? =2????
∴cos A= ????????????????= 2????????= ????????
?
BY YUSHEN
练一练
02
在 Rt△ABC 中,∠C=90°,若∠A=45°且 BC=2,求cosA=?
A
B
C
∵ ∠C=90°,∠A=45°
∴ Rt△ABC为等腰直角三角形,BC=AC=2
由勾股定理得AB= ????????????+???????????? =2????
∴cos A= ????????????????= 22????= ????????
?
若∠A=60°且AC=2,求cosA=?
BY YUSHEN
练一练
02
在 Rt△ABC 中,∠C=90°,若∠A=30°且 BC=2,求tanA=?
A
B
C
∵ ∠C=90°,∠A=30°
而在Rt△ABC中, 30°角所对的边等于斜边的一边
∴AB=4, 由勾股定理得AC= ????????????????????????? =2????
∴tanA= ????????????????= ????2????= ????????
?
BY YUSHEN
练一练
02
在 Rt△ABC 中,∠C=90°,若∠A=45°且 BC=2,求tanA=?
A
B
C
∵ ∠C=90°,∠A=45°
∴ Rt△ABC为等腰直角三角形,BC=AC=2
∴ tanA= ?????????????????= ????
?
若∠A=60°,求tanA=?
BY YUSHEN
练一练
02
在 Rt△ABC 中,∠C=90°,若AB=10,BC=6,求tanA,sinA,cosA的值?
A
B
C
由勾股定理得AC= ????????2?????????2 =8
因此sinA= ???????????????? = 35
cosA= ?????????????????= 45
tanA= ?????????????????= 34
?
BY YUSHEN
变式
02
在 Rt△ABC 中,∠C=90°,若sinA= 35 ,求tanA,cosA的值?
?
A
B
C
BY YUSHEN
练一练
02
1.在△ABC中∠C=90°,tanA=33,则cosB=_____.
?
【答案】12
【详解】
解:∵在Rt△ABC中,∠C=90°,tanA=33,
设a=3x,b=3x,则c=23x,
∴cosB=????????=12.
故答案为:12.
?
2.在????????????????????????中,∠????=90°,如果????????=6,????????????????=23,那么????????= ;
?
【答案】4
【解析】
因为在????????????????????????中,∠????=90°,所以????????????????=????????????????=23,
所以????????=23????????=23×6=4.
?
BY YUSHEN
练一练
02
3. Rt△ABC中,∠C=90°,cosA=35,AC=6cm,那么BC等于_____.
?
【答案】8cm
【详解】
在????????△????????????中,∵?????????????????=????????????????,
∴????????=????????????????????????=635=10????????,
则????????=????????2?????????2=102?62=8????????.
故答案为:8????????.
?
4.(2019·四川东辰国际学校中考模拟)如图,正方形网格中每个小正方形的边长都是1,若点A、B、C都在格点上,则tan∠BAC的值是_____.
解:连接CD,∵∠CAD=∠ACD=45°,
∴∠ADC=90°,
由勾股定理得:AD=CD=12+11=2,
∴tan∠BAC=22=1,
故答案为:1.
?
BY YUSHEN
课后回顾
理解余弦的概念
01
理解正切的概念
02
利用余弦、正切
进行相关计算
03
BY YUSHEN
谢谢观看!
TOPIC 28.1 ACUTE TRIANGLE (SINE, COSINE, TANGENT VALUE OF SPECIAL ANGLE)
