22.1.2 二次函数y=ax2的图象和性质 同步练习(含答案)
文档属性
| 名称 | 22.1.2 二次函数y=ax2的图象和性质 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-02 00:00:00 | ||
图片预览

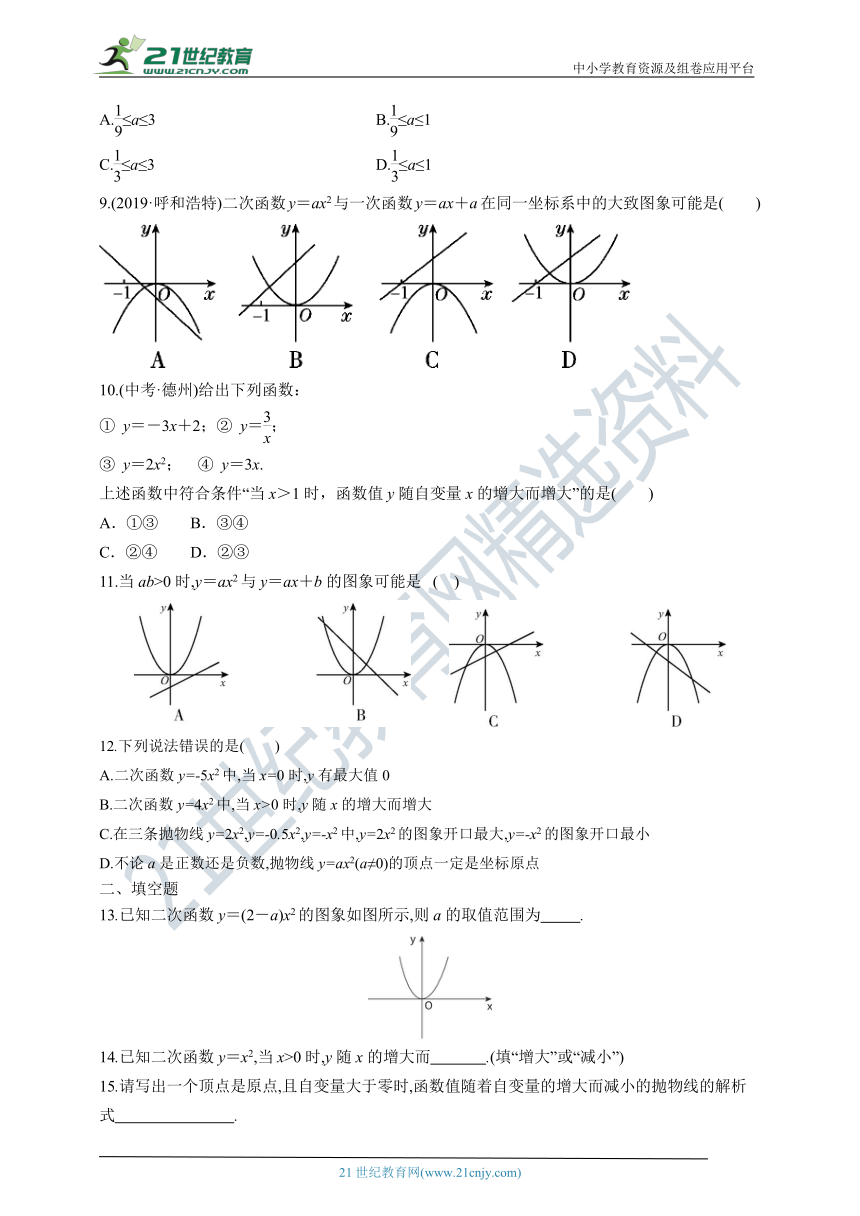

文档简介
22.1.2 二次函数y=ax2的图象和性质
一、选择题
1.二次函数y=x2的对称轴是 ( )
A.直线y=1 B.直线x=1
C.y轴 D.x轴
2.下列图象中,是二次函数y=-2x2的图象的是 ( )
3.函数y=4x2的图象的顶点坐标为 ( )
A.(1,-4) B.(0,0)
C.(0,4) D.(4,0)
4.若二次函数y=ax2的图象经过点P(-2,4),则该图象必经过点 ( )
A.(2,4) B.(-2,-4)
C.(-4,2) D.(4,-2)
5.下列函数中,当x<0时,函数值y随x的增大而增大的有( )
①y=3x;②y=-4x-3;③y=-2x2;④y=5x2.
A.1个 B.2个 C.3个 D.4个
6.已知点A(-3,y1),B(-1,y2),C(2,y3)在抛物线y=23x2上,则y1,y2,y3的大小关系是 ( )
A.y1y2>y3
C.y17.二次函数y=ax2与一次函数y=-ax在同一平面直角坐标系中的图象可能是 ( )
8.(2020·南充)如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3).若抛物线y=ax2与正方形有公共点,则实数a的取值范围是( )
A.≤a≤3 B.≤a≤1
C.≤a≤3 D.≤a≤1
9.(2019·呼和浩特)二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是( )
10.(中考·德州)给出下列函数:
① y=-3x+2;② y=;
③ y=2x2; ④ y=3x.
上述函数中符合条件“当x>1时,函数值y随自变量x的增大而增大”的是( )
A.①③ B.③④
C.②④ D.②③
11.当ab>0时,y=ax2与y=ax+b的图象可能是 ( )
12.下列说法错误的是( )
A.二次函数y=-5x2中,当x=0时,y有最大值0
B.二次函数y=4x2中,当x>0时,y随x的增大而增大
C.在三条抛物线y=2x2,y=-0.5x2,y=-x2中,y=2x2的图象开口最大,y=-x2的图象开口最小
D.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
二、填空题
13.已知二次函数y=(2-a)x2的图象如图所示,则a的取值范围为 .?
14.已知二次函数y=x2,当x>0时,y随x的增大而 .(填“增大”或“减小”)?
15.请写出一个顶点是原点,且自变量大于零时,函数值随着自变量的增大而减小的抛物线的解析式 .?
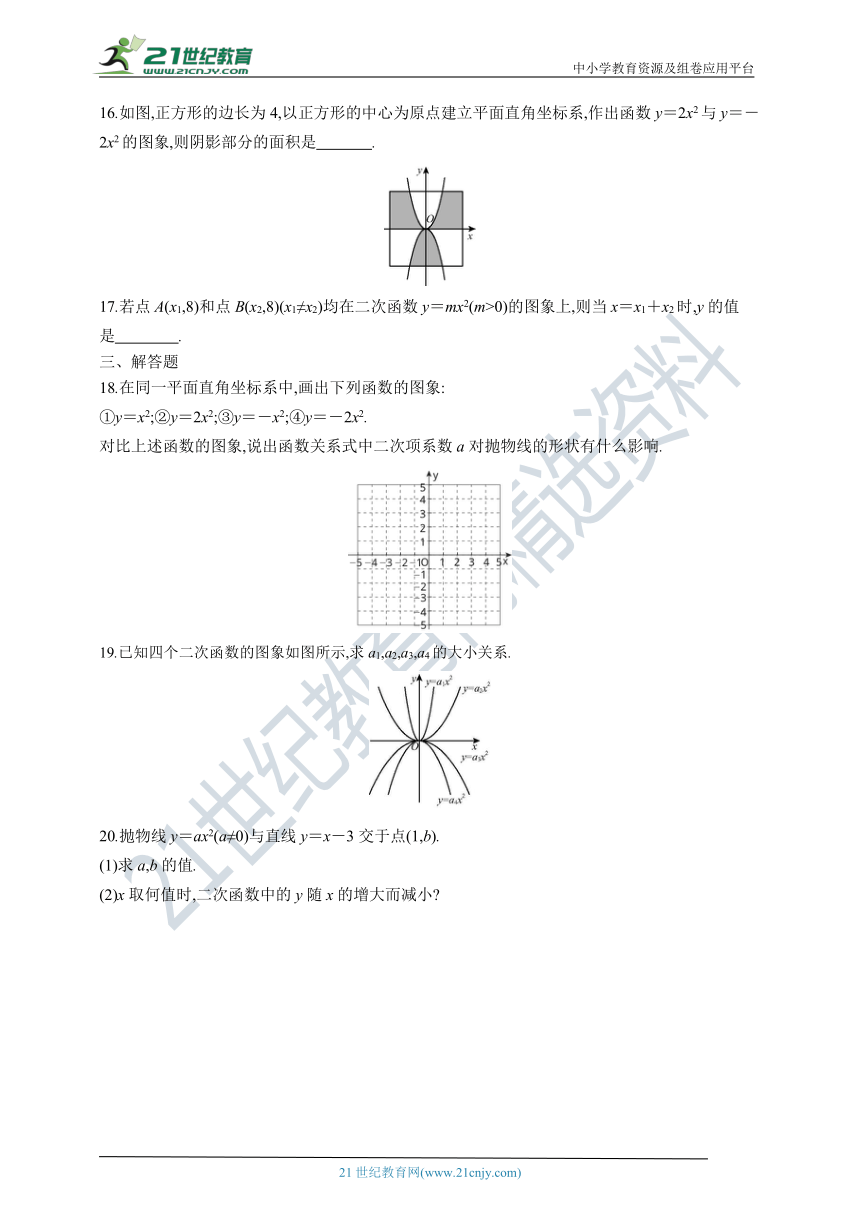
16.如图,正方形的边长为4,以正方形的中心为原点建立平面直角坐标系,作出函数y=2x2与y=-2x2的图象,则阴影部分的面积是 .?
17.若点A(x1,8)和点B(x2,8)(x1≠x2)均在二次函数y=mx2(m>0)的图象上,则当x=x1+x2时,y的值是 .?
三、解答题
18.在同一平面直角坐标系中,画出下列函数的图象:
①y=x2;②y=2x2;③y=-x2;④y=-2x2.
对比上述函数的图象,说出函数关系式中二次项系数a对抛物线的形状有什么影响.
19.已知四个二次函数的图象如图所示,求a1,a2,a3,a4的大小关系.
20.抛物线y=ax2(a≠0)与直线y=x-3交于点(1,b).
(1)求a,b的值.
(2)x取何值时,二次函数中的y随x的增大而减小?
21.已知一次函数y=ax+b的图象上有A,B两点,它们的横坐标分别是3,-1.若二次函数y=13x2的图象经过A,B两点.
(1)请求出此一次函数的解析式;
(2)设该二次函数的顶点为C,求△ABC的面积.
22.如图,过点F(0,-1)的直线y=kx+b(k≠0)与抛物线y=-14x2交于A(x1,y1),B(x2,y2)两点.
(1)求b的值;
(2)求x1x2的值.
23.定义:若抛物线y的顶点为P,点A的坐标为(a,a)(a是常数,且a≠0),我们把线段PA称为抛物线y的顶割线.已知抛物线y=mx2(m≠0).
(1)求抛物线y的顶割线所在直线的函数解析式;
(2)若抛物线y的顶割线长为22,且点A在抛物线y上,求m的值.
24.如图,一次函数y=kx+b的图象与二次函数y=ax2的图象交于点A(1,m)和B(-2,4),与y轴交于点C.求:
(1)a,b,k的值;
(2)△AOB的面积.
参考答案
一、选择题
1.二次函数y=x2的对称轴是 (C)
A.直线y=1 B.直线x=1
C.y轴 D.x轴
2.下列图象中,是二次函数y=-2x2的图象的是 (D)
3.函数y=4x2的图象的顶点坐标为 (B)
A.(1,-4) B.(0,0)
C.(0,4) D.(4,0)
4.若二次函数y=ax2的图象经过点P(-2,4),则该图象必经过点 (A)
A.(2,4) B.(-2,-4)
C.(-4,2) D.(4,-2)
5.下列函数中,当x<0时,函数值y随x的增大而增大的有( B )
①y=3x;②y=-4x-3;③y=-2x2;④y=5x2.
A.1个 B.2个 C.3个 D.4个
6.已知点A(-3,y1),B(-1,y2),C(2,y3)在抛物线y=23x2上,则y1,y2,y3的大小关系是 (D)
A.y1y2>y3
C.y17.二次函数y=ax2与一次函数y=-ax在同一平面直角坐标系中的图象可能是 (B)
8.(2020·南充)如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3).若抛物线y=ax2与正方形有公共点,则实数a的取值范围是( )
A.≤a≤3 B.≤a≤1
C.≤a≤3 D.≤a≤1
【点拨】当抛物线经过点(1,3)时,a=3;
当抛物线经过点(3,1)时,a=.
观察图象可知≤a≤3.
【答案】A
9.(2019·呼和浩特)二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是( )
【点拨】分a>0和a<0两种情况:
当a>0时,y=ax2的图象开口向上,y=ax+a的图象经过第一、二、三象限且过点(-1,0);
当a<0时,y=ax2的图象开口向下,y=ax+a的图象经过第二、三、四象限且过点(-1,0).
综上可知,应选D.
【答案】D
10.(中考·德州)给出下列函数:
① y=-3x+2;② y=;
③ y=2x2; ④ y=3x.
上述函数中符合条件“当x>1时,函数值y随自变量x的增大而增大”的是( )
A.①③ B.③④
C.②④ D.②③
【点拨】对于①③④,可利用性质判断.对于②,可利用特殊值法判断.分别令x等于1和2,求得y的值为3和1.5,不符合题目条件.
【答案】B
11.当ab>0时,y=ax2与y=ax+b的图象可能是 (D)
12.下列说法错误的是( C )
A.二次函数y=-5x2中,当x=0时,y有最大值0
B.二次函数y=4x2中,当x>0时,y随x的增大而增大
C.在三条抛物线y=2x2,y=-0.5x2,y=-x2中,y=2x2的图象开口最大,y=-x2的图象开口最小
D.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
二、填空题
13.已知二次函数y=(2-a)x2的图象如图所示,则a的取值范围为 a<2 .?
14.已知二次函数y=x2,当x>0时,y随x的增大而 增大 .(填“增大”或“减小”)?
15.请写出一个顶点是原点,且自变量大于零时,函数值随着自变量的增大而减小的抛物线的解析式 y=-x2(答案不唯一) .?
16.如图,正方形的边长为4,以正方形的中心为原点建立平面直角坐标系,作出函数y=2x2与y=-2x2的图象,则阴影部分的面积是 8 .?
17.若点A(x1,8)和点B(x2,8)(x1≠x2)均在二次函数y=mx2(m>0)的图象上,则当x=x1+x2时,y的值是 0 .?
三、解答题
18.在同一平面直角坐标系中,画出下列函数的图象:
①y=x2;②y=2x2;③y=-x2;④y=-2x2.
对比上述函数的图象,说出函数关系式中二次项系数a对抛物线的形状有什么影响.
图略.由图象可知,a的绝对值相同,两条抛物线的形状就相同,a>0时,开口向上,a<0时开口向下;|a|越大,开口越小.
19.已知四个二次函数的图象如图所示,求a1,a2,a3,a4的大小关系.
解:a1>a2>a3>a4.
20.抛物线y=ax2(a≠0)与直线y=x-3交于点(1,b).
(1)求a,b的值.
(2)x取何值时,二次函数中的y随x的增大而减小?
解:(1)把点(1,b)代入y=x-3,得b=1-3=-2,
∴抛物线与直线的交点的坐标为(1,-2),
把点(1,-2)代入y=ax2,得a=-2.
(2)由(1)知y=-2x2,∴抛物线开口向下,且对称轴为y轴,
∴当x>0时,y随x的增大而减小.
21.已知一次函数y=ax+b的图象上有A,B两点,它们的横坐标分别是3,-1.若二次函数y=13x2的图象经过A,B两点.
(1)请求出此一次函数的解析式;
(2)设该二次函数的顶点为C,求△ABC的面积.
解:(1)一次函数的解析式为y=23x+1.
(2)∵二次函数的解析式为y=13x2,∴点C的坐标为(0,0).
设一次函数与y轴的交点为D,则点D的坐标为(0,1),
∴CD=1,∴S△ABC=12CD·(xA-xB)=12×1×4=2.
22.如图,过点F(0,-1)的直线y=kx+b(k≠0)与抛物线y=-14x2交于A(x1,y1),B(x2,y2)两点.
(1)求b的值;
(2)求x1x2的值.
解:(1)b=-1.
(2)因为b=-1,所以直线的解析式为y=kx-1,联立y=kx-1,y=-14x2,则-14x2-kx+1=0,所以x1x2=-4.
23.定义:若抛物线y的顶点为P,点A的坐标为(a,a)(a是常数,且a≠0),我们把线段PA称为抛物线y的顶割线.已知抛物线y=mx2(m≠0).
(1)求抛物线y的顶割线所在直线的函数解析式;
(2)若抛物线y的顶割线长为22,且点A在抛物线y上,求m的值.
解:(1)∵抛物线y=mx2(m≠0)的顶点坐标是(0,0),
∴设顶割线所在直线的函数解析式为y=kx,把点A(a,a)代入y=kx,得a=ka,∵a≠0,∴k=1,
∴抛物线y的顶割线所在直线的函数解析式为y=x.
(2)∵抛物线y的顶割线长为22,∴PA=22,
∴a2+a2=(22)2,解得a=-2或a=2,
∴点A的坐标为(-2,-2)或(2,2),
分别代入y=mx2,得m=-12或m=12.
24.如图,一次函数y=kx+b的图象与二次函数y=ax2的图象交于点A(1,m)和B(-2,4),与y轴交于点C.求:
(1)a,b,k的值;
解:把点B(-2,4)的坐标代入y=ax2,得4=4a,∴a=1.
∴二次函数的解析式是y=x2.
把点A(1,m)的坐标代入y=x2,得m=1,∴A(1,1).
把A(1,1)和B(-2,4)的坐标分别代入y=kx+b,
得解得
∴a=1,b=2,k=-1.
(2)△AOB的面积.
解:令y=-x+2中x=0,则y=2,∴C(0,2).
∴OC=2.
∴S△AOC=OC·|1|=×2×1=1,S△BOC=OC·|-2|=×2×2=2.
∴S△AOB=S△AOC+S△BOC=1+2=3.
一、选择题
1.二次函数y=x2的对称轴是 ( )
A.直线y=1 B.直线x=1
C.y轴 D.x轴
2.下列图象中,是二次函数y=-2x2的图象的是 ( )
3.函数y=4x2的图象的顶点坐标为 ( )
A.(1,-4) B.(0,0)
C.(0,4) D.(4,0)
4.若二次函数y=ax2的图象经过点P(-2,4),则该图象必经过点 ( )
A.(2,4) B.(-2,-4)
C.(-4,2) D.(4,-2)
5.下列函数中,当x<0时,函数值y随x的增大而增大的有( )
①y=3x;②y=-4x-3;③y=-2x2;④y=5x2.
A.1个 B.2个 C.3个 D.4个
6.已知点A(-3,y1),B(-1,y2),C(2,y3)在抛物线y=23x2上,则y1,y2,y3的大小关系是 ( )
A.y1
C.y1
8.(2020·南充)如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3).若抛物线y=ax2与正方形有公共点,则实数a的取值范围是( )
A.≤a≤3 B.≤a≤1
C.≤a≤3 D.≤a≤1
9.(2019·呼和浩特)二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是( )
10.(中考·德州)给出下列函数:
① y=-3x+2;② y=;
③ y=2x2; ④ y=3x.
上述函数中符合条件“当x>1时,函数值y随自变量x的增大而增大”的是( )
A.①③ B.③④
C.②④ D.②③
11.当ab>0时,y=ax2与y=ax+b的图象可能是 ( )
12.下列说法错误的是( )
A.二次函数y=-5x2中,当x=0时,y有最大值0
B.二次函数y=4x2中,当x>0时,y随x的增大而增大
C.在三条抛物线y=2x2,y=-0.5x2,y=-x2中,y=2x2的图象开口最大,y=-x2的图象开口最小
D.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
二、填空题
13.已知二次函数y=(2-a)x2的图象如图所示,则a的取值范围为 .?
14.已知二次函数y=x2,当x>0时,y随x的增大而 .(填“增大”或“减小”)?
15.请写出一个顶点是原点,且自变量大于零时,函数值随着自变量的增大而减小的抛物线的解析式 .?
16.如图,正方形的边长为4,以正方形的中心为原点建立平面直角坐标系,作出函数y=2x2与y=-2x2的图象,则阴影部分的面积是 .?
17.若点A(x1,8)和点B(x2,8)(x1≠x2)均在二次函数y=mx2(m>0)的图象上,则当x=x1+x2时,y的值是 .?
三、解答题
18.在同一平面直角坐标系中,画出下列函数的图象:
①y=x2;②y=2x2;③y=-x2;④y=-2x2.
对比上述函数的图象,说出函数关系式中二次项系数a对抛物线的形状有什么影响.
19.已知四个二次函数的图象如图所示,求a1,a2,a3,a4的大小关系.
20.抛物线y=ax2(a≠0)与直线y=x-3交于点(1,b).
(1)求a,b的值.
(2)x取何值时,二次函数中的y随x的增大而减小?
21.已知一次函数y=ax+b的图象上有A,B两点,它们的横坐标分别是3,-1.若二次函数y=13x2的图象经过A,B两点.
(1)请求出此一次函数的解析式;
(2)设该二次函数的顶点为C,求△ABC的面积.
22.如图,过点F(0,-1)的直线y=kx+b(k≠0)与抛物线y=-14x2交于A(x1,y1),B(x2,y2)两点.
(1)求b的值;
(2)求x1x2的值.
23.定义:若抛物线y的顶点为P,点A的坐标为(a,a)(a是常数,且a≠0),我们把线段PA称为抛物线y的顶割线.已知抛物线y=mx2(m≠0).
(1)求抛物线y的顶割线所在直线的函数解析式;
(2)若抛物线y的顶割线长为22,且点A在抛物线y上,求m的值.
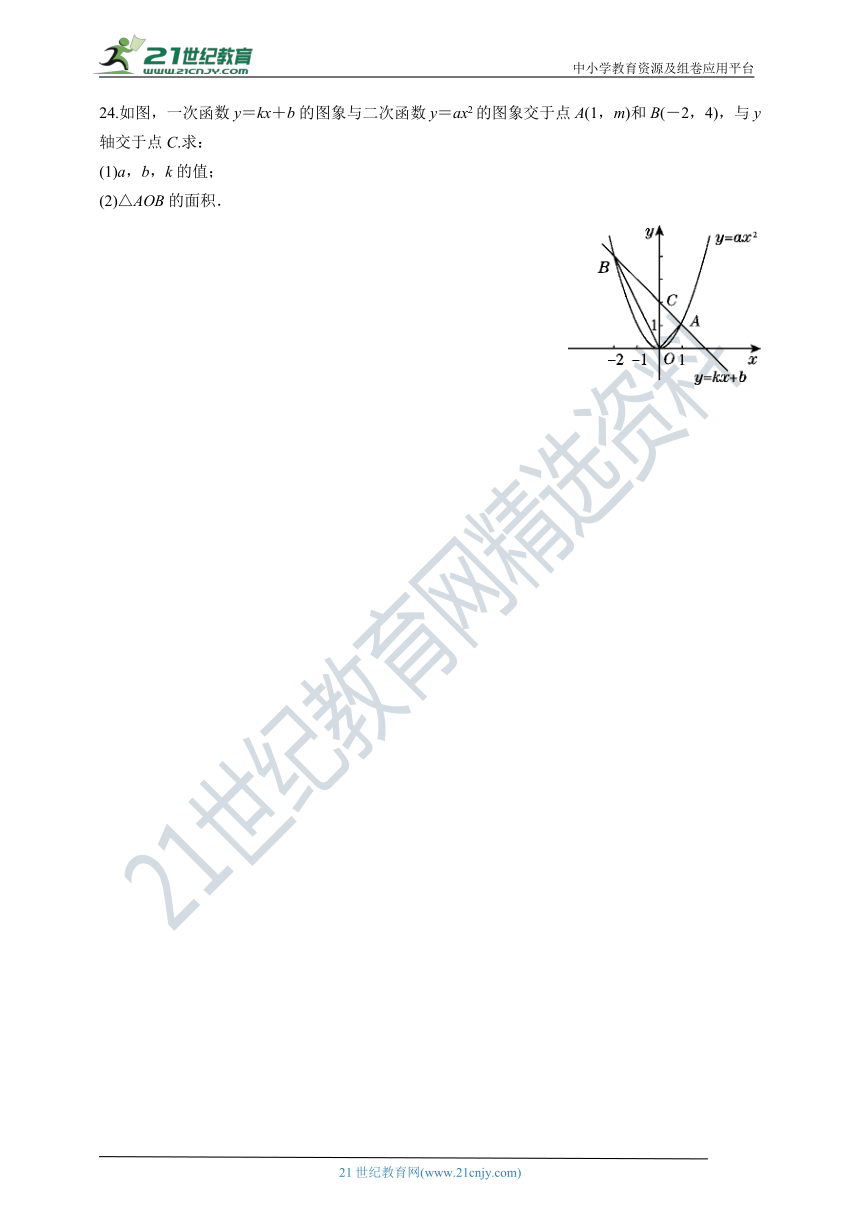
24.如图,一次函数y=kx+b的图象与二次函数y=ax2的图象交于点A(1,m)和B(-2,4),与y轴交于点C.求:
(1)a,b,k的值;
(2)△AOB的面积.
参考答案
一、选择题
1.二次函数y=x2的对称轴是 (C)
A.直线y=1 B.直线x=1
C.y轴 D.x轴
2.下列图象中,是二次函数y=-2x2的图象的是 (D)
3.函数y=4x2的图象的顶点坐标为 (B)
A.(1,-4) B.(0,0)
C.(0,4) D.(4,0)
4.若二次函数y=ax2的图象经过点P(-2,4),则该图象必经过点 (A)
A.(2,4) B.(-2,-4)
C.(-4,2) D.(4,-2)
5.下列函数中,当x<0时,函数值y随x的增大而增大的有( B )
①y=3x;②y=-4x-3;③y=-2x2;④y=5x2.
A.1个 B.2个 C.3个 D.4个
6.已知点A(-3,y1),B(-1,y2),C(2,y3)在抛物线y=23x2上,则y1,y2,y3的大小关系是 (D)
A.y1
C.y1
8.(2020·南充)如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3).若抛物线y=ax2与正方形有公共点,则实数a的取值范围是( )
A.≤a≤3 B.≤a≤1
C.≤a≤3 D.≤a≤1
【点拨】当抛物线经过点(1,3)时,a=3;
当抛物线经过点(3,1)时,a=.
观察图象可知≤a≤3.
【答案】A
9.(2019·呼和浩特)二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是( )
【点拨】分a>0和a<0两种情况:
当a>0时,y=ax2的图象开口向上,y=ax+a的图象经过第一、二、三象限且过点(-1,0);
当a<0时,y=ax2的图象开口向下,y=ax+a的图象经过第二、三、四象限且过点(-1,0).
综上可知,应选D.
【答案】D
10.(中考·德州)给出下列函数:
① y=-3x+2;② y=;
③ y=2x2; ④ y=3x.
上述函数中符合条件“当x>1时,函数值y随自变量x的增大而增大”的是( )
A.①③ B.③④
C.②④ D.②③
【点拨】对于①③④,可利用性质判断.对于②,可利用特殊值法判断.分别令x等于1和2,求得y的值为3和1.5,不符合题目条件.
【答案】B
11.当ab>0时,y=ax2与y=ax+b的图象可能是 (D)
12.下列说法错误的是( C )
A.二次函数y=-5x2中,当x=0时,y有最大值0
B.二次函数y=4x2中,当x>0时,y随x的增大而增大
C.在三条抛物线y=2x2,y=-0.5x2,y=-x2中,y=2x2的图象开口最大,y=-x2的图象开口最小
D.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
二、填空题
13.已知二次函数y=(2-a)x2的图象如图所示,则a的取值范围为 a<2 .?
14.已知二次函数y=x2,当x>0时,y随x的增大而 增大 .(填“增大”或“减小”)?
15.请写出一个顶点是原点,且自变量大于零时,函数值随着自变量的增大而减小的抛物线的解析式 y=-x2(答案不唯一) .?
16.如图,正方形的边长为4,以正方形的中心为原点建立平面直角坐标系,作出函数y=2x2与y=-2x2的图象,则阴影部分的面积是 8 .?
17.若点A(x1,8)和点B(x2,8)(x1≠x2)均在二次函数y=mx2(m>0)的图象上,则当x=x1+x2时,y的值是 0 .?
三、解答题
18.在同一平面直角坐标系中,画出下列函数的图象:
①y=x2;②y=2x2;③y=-x2;④y=-2x2.
对比上述函数的图象,说出函数关系式中二次项系数a对抛物线的形状有什么影响.
图略.由图象可知,a的绝对值相同,两条抛物线的形状就相同,a>0时,开口向上,a<0时开口向下;|a|越大,开口越小.
19.已知四个二次函数的图象如图所示,求a1,a2,a3,a4的大小关系.
解:a1>a2>a3>a4.
20.抛物线y=ax2(a≠0)与直线y=x-3交于点(1,b).
(1)求a,b的值.
(2)x取何值时,二次函数中的y随x的增大而减小?
解:(1)把点(1,b)代入y=x-3,得b=1-3=-2,
∴抛物线与直线的交点的坐标为(1,-2),
把点(1,-2)代入y=ax2,得a=-2.
(2)由(1)知y=-2x2,∴抛物线开口向下,且对称轴为y轴,
∴当x>0时,y随x的增大而减小.
21.已知一次函数y=ax+b的图象上有A,B两点,它们的横坐标分别是3,-1.若二次函数y=13x2的图象经过A,B两点.
(1)请求出此一次函数的解析式;
(2)设该二次函数的顶点为C,求△ABC的面积.
解:(1)一次函数的解析式为y=23x+1.
(2)∵二次函数的解析式为y=13x2,∴点C的坐标为(0,0).
设一次函数与y轴的交点为D,则点D的坐标为(0,1),
∴CD=1,∴S△ABC=12CD·(xA-xB)=12×1×4=2.
22.如图,过点F(0,-1)的直线y=kx+b(k≠0)与抛物线y=-14x2交于A(x1,y1),B(x2,y2)两点.
(1)求b的值;
(2)求x1x2的值.
解:(1)b=-1.
(2)因为b=-1,所以直线的解析式为y=kx-1,联立y=kx-1,y=-14x2,则-14x2-kx+1=0,所以x1x2=-4.
23.定义:若抛物线y的顶点为P,点A的坐标为(a,a)(a是常数,且a≠0),我们把线段PA称为抛物线y的顶割线.已知抛物线y=mx2(m≠0).
(1)求抛物线y的顶割线所在直线的函数解析式;
(2)若抛物线y的顶割线长为22,且点A在抛物线y上,求m的值.
解:(1)∵抛物线y=mx2(m≠0)的顶点坐标是(0,0),
∴设顶割线所在直线的函数解析式为y=kx,把点A(a,a)代入y=kx,得a=ka,∵a≠0,∴k=1,
∴抛物线y的顶割线所在直线的函数解析式为y=x.
(2)∵抛物线y的顶割线长为22,∴PA=22,
∴a2+a2=(22)2,解得a=-2或a=2,
∴点A的坐标为(-2,-2)或(2,2),
分别代入y=mx2,得m=-12或m=12.
24.如图,一次函数y=kx+b的图象与二次函数y=ax2的图象交于点A(1,m)和B(-2,4),与y轴交于点C.求:
(1)a,b,k的值;
解:把点B(-2,4)的坐标代入y=ax2,得4=4a,∴a=1.
∴二次函数的解析式是y=x2.
把点A(1,m)的坐标代入y=x2,得m=1,∴A(1,1).
把A(1,1)和B(-2,4)的坐标分别代入y=kx+b,
得解得
∴a=1,b=2,k=-1.
(2)△AOB的面积.
解:令y=-x+2中x=0,则y=2,∴C(0,2).
∴OC=2.
∴S△AOC=OC·|1|=×2×1=1,S△BOC=OC·|-2|=×2×2=2.
∴S△AOB=S△AOC+S△BOC=1+2=3.
同课章节目录
