辽宁省大连市本溪县高中2020-2021学年高一下学期6月月考数学试卷 Word版含答案
文档属性
| 名称 | 辽宁省大连市本溪县高中2020-2021学年高一下学期6月月考数学试卷 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 873.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 00:00:00 | ||
图片预览



文档简介
本溪县高中2020-2021学年高一下学期6月月考
数学试卷
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设复数满足,则的虚部为( )
A B C D
2.设,均为单位向量,当,的夹角为时,在方向上的投影数量为( )
A. B. C. D.
3.的内角,,所对的边分别是,,,若,,,则等于( )
A.1 B. C. D.2
4. 已知函数,则下列说法正确的是( )
A.f(x)的最小正周期为2π B.f(x)的最大值为
C.f(x)在上单调递增 D.f(x)的图象关于直线x对称
5. 若,则( )
A. B. C. D.
6. 在四棱锥P—ABCD中,底面ABCD是边长为的正方形,且PA=PB=PC=PD=2.若点E、F、G分别为棱PB、PC、PD上的动点(不包含端点P),则AE+EF+FG+GA的最小值为 ( )
A B C D 4
7.设锐角的内角所对的边分别为,若,则的取值范围为( )
A.(1,9] B.(3,9] C.(5,9] D.(7,9]
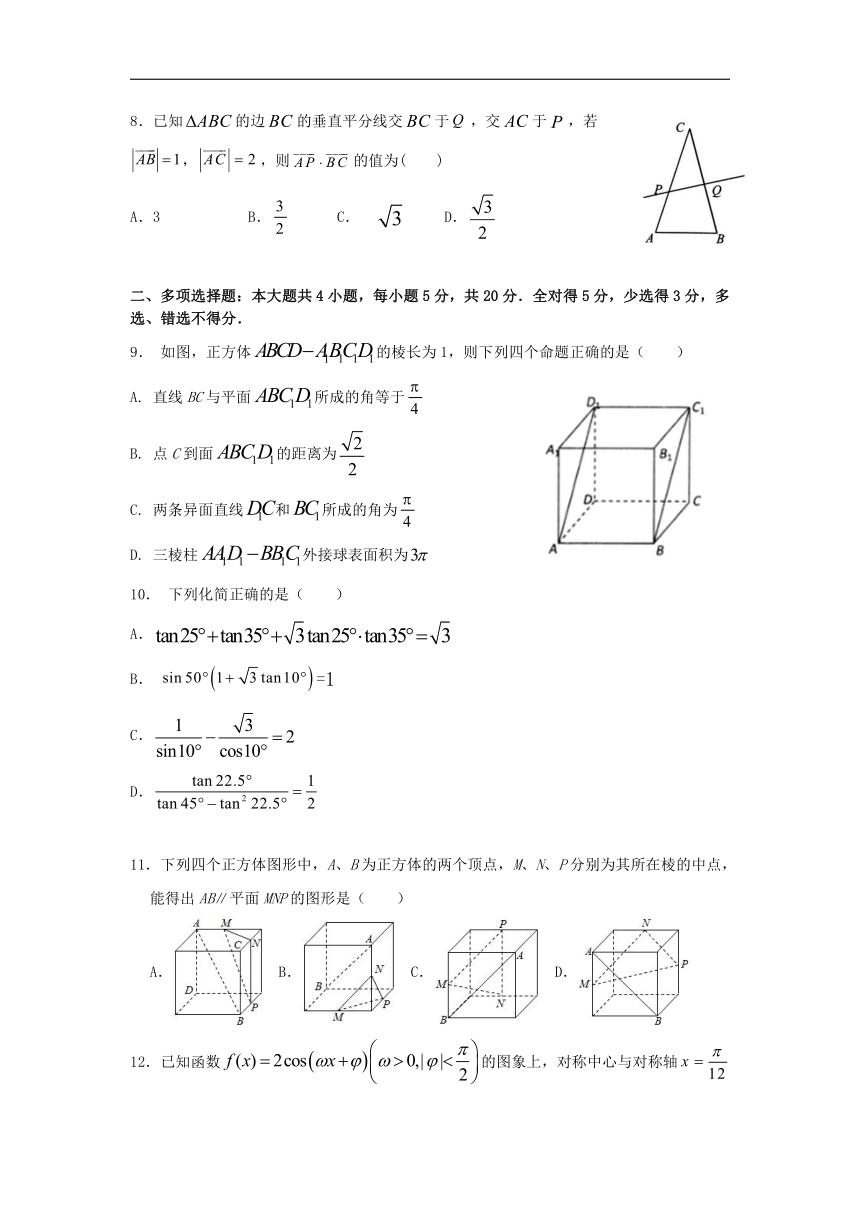
8.已知的边的垂直平分线交于,交于,若,,则的值为( )
A.3 B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.全对得5分,少选得3分,多选、错选不得分.
9. 如图,正方体的棱长为1,则下列四个命题正确的是( )
A. 直线BC与平面所成的角等于
B. 点C到面的距离为
C. 两条异面直线和所成的角为
D. 三棱柱外接球表面积为
10. 下列化简正确的是( )
A.
B. =1
C.
D.
11.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形是( )
A. B. C. D.
12.已知函数的图象上,对称中心与对称轴的最小距离为,则下列结论正确的是( )
A. B.当时,
C.若,则
D.若,,则的值为
三.填空题:本大题共4小题,每小题5分,共20分.
13.若,则=_____.
14.已知是三条不同的直线,是三个不同的平面,有下列命题:
① ②若则
③则 ④直线,直线,那么
⑤若,则 ⑥若,则,
其中正确的说法为__________(填序号)
15.已知,若在内单调,则 的取值范围是
16.已知向量满足,,则的取值范围是_________.
四.解答题:本大题共5小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤。
17.(本题满分10分)已知复数z=a+i(a>0,a∈R),i为虚数单位,且复数为实数.
(1)求复数z ;
(2)在复平面内,若复数(m+z)2对应的点在第一象限,求实数m的取值范围.
18.(本题满分12分)已知.
(1)求的值;
(2)若,且,求的值.
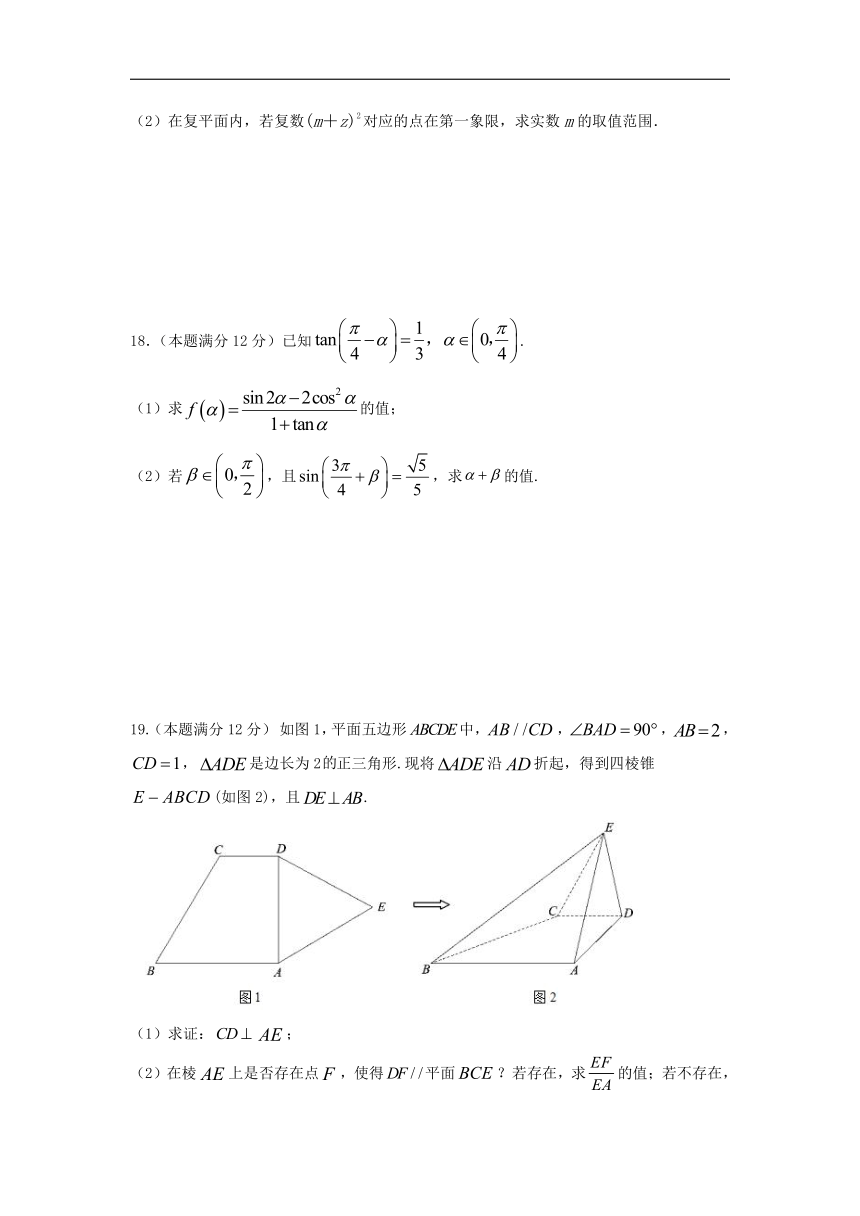
19.(本题满分12分) 如图1,平面五边形中,,,,,是边长为2正三角形.现将沿折起,得到四棱锥(如图2),且.
(1)求证:;
(2)在棱上是否存在点,使得平面?若存在,求的值;若不存在,请说明理由.
20.(本题满分12分)已知函数.
(Ⅰ)求函数在的单调递减区间;
(Ⅱ)在中,内角,,,的对边分别为,,,已知,·=4且D是边BC的中点,AD=,求的周长.
21.(本题满分12分)已知函数.其图象的一个对称中心是,将的图象向左平移个单位长度后得到函数的图象.
(1)求函数的解析式;
(2)若对任意,当时,都有,求实数的最大值.
22.(本题满分12分)如图,正三棱柱的棱长均为2,M是侧棱的中点.
(1)在图中作出平面与平面的交线l(简要说明),并证明平面;
(2)求C点到平面的距离.
本溪县高中2020-2021学年高一下学期6月月考
数学试卷答案
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.C 2.B 3.D 4.B 5.A 6.C 7.D 8.B
二、多项选择题:本大题共4小题,每小题5分,共20分.全对得5分,少选得3分,多选、错选不得分.
9. ABD 10.ABD 11.AD. 12.BD
三.填空题:本大题共4小题,每小题5分,共20分.
13. 14.①⑥ 15. . 16.
四.解答题:本大题共5小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤。
17.(本题满分10分)
【解析】(1)因为z=a+i(a>0),所以z+=a+i+
=a+i+=a+i+=,
由于复数z+为实数,所以1-=0,
因为a>0,解得a=1,因此,z=1+i. 5分
(2)由题意(m+z)2=(m+1+i)2=(m+1)2-1+2(m+1)i=(m2+2m)+2(m+1)i,
由于复数(m+z)2对应的点在第一象限,则,解得m>0.
因此,实数m的取值范围是(0,+∞). 10分
18. (本题满分12分)
解:(1)∵,∴,解得.
∴; 6分
(2)∵,且∴
∴,
∴,∴.∴.
∴,
又∵, ∴. 12分
19. (本题满分12分)
【详解】(1)证明:由已知得,,因为,
所以平面. 又因为,所以 因为平面ADE
5分
(2)在棱上存在点,使得平面, 此时. 6分
理由如下:假设存在点为的中点,设的中点为,连接,,
则,. 因为,且,
所以,且,
所以四边形是平行四边形,
所以. 因为平面,
且平面,所以平面.
所以在棱上存在点,使得平面,
此时. 12分
20.(本题满分12分)
解(1)由已知得 …………3分
又
函数在的单调递减区间为和. …………6分
(2)由(1)知中, A∈(0,π),
又,即 …………9分
由·=4,得bccos A=4,∴bc=8 ①, ∵=(+),∴=(+2·+),
∴7=c2+2bc·cos+b2 ②, 由① ②得:
所以周长为
21. (本题满分12分)
【详解】(1)由题意,得,解得,
又,∴,∴,
从而. 5分
(2)对任意,,且,
,
即在上单调递增,,
由,得,
即的单调增区间为,
由于,
∴当时,,从而,
∴实数t的最大值为. 12分
22. (本题满分12分)
【详解】(1)延长,交CA的延长线于N,连接BN,
N在直线CA上,平面ABC,平面ABC,
又平面ABC内,∴直线平面ABC,
直线C1M,直线C1M?平面MBC1,平面MBC1,
又平面MBC1,∴直线平面MBC1,
平面,平面;
为AA1的中点,CC1AA1,,
,又∵正三棱柱ABC-A1B1C1各棱长均为2,
,C,B,N在以A为圆心半径为2的圆周上,直径为CN,
由于直径所对的圆周角为直角,为直角, 即NB⊥BC,
又∵正三棱柱的侧棱BB1⊥底面ABC,直线平面ABC,∴BB1⊥直线BN,
又∵BB1∩BC=B,平面BB1C1C,平面BB1C1C,∴直线BN⊥平面BB1C1C,
即直线l⊥平面BB1C1C. 7分
(2)由(1)知平面,平面,所以,
,,
所以,
,
设到平面的距离为h,因为,所以,
即 解得,点C到平面的距离为. 12分
数学试卷
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设复数满足,则的虚部为( )
A B C D
2.设,均为单位向量,当,的夹角为时,在方向上的投影数量为( )
A. B. C. D.
3.的内角,,所对的边分别是,,,若,,,则等于( )
A.1 B. C. D.2
4. 已知函数,则下列说法正确的是( )
A.f(x)的最小正周期为2π B.f(x)的最大值为
C.f(x)在上单调递增 D.f(x)的图象关于直线x对称
5. 若,则( )
A. B. C. D.
6. 在四棱锥P—ABCD中,底面ABCD是边长为的正方形,且PA=PB=PC=PD=2.若点E、F、G分别为棱PB、PC、PD上的动点(不包含端点P),则AE+EF+FG+GA的最小值为 ( )
A B C D 4
7.设锐角的内角所对的边分别为,若,则的取值范围为( )
A.(1,9] B.(3,9] C.(5,9] D.(7,9]
8.已知的边的垂直平分线交于,交于,若,,则的值为( )
A.3 B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.全对得5分,少选得3分,多选、错选不得分.
9. 如图,正方体的棱长为1,则下列四个命题正确的是( )
A. 直线BC与平面所成的角等于
B. 点C到面的距离为
C. 两条异面直线和所成的角为
D. 三棱柱外接球表面积为
10. 下列化简正确的是( )
A.
B. =1
C.
D.
11.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形是( )
A. B. C. D.
12.已知函数的图象上,对称中心与对称轴的最小距离为,则下列结论正确的是( )
A. B.当时,
C.若,则
D.若,,则的值为
三.填空题:本大题共4小题,每小题5分,共20分.
13.若,则=_____.
14.已知是三条不同的直线,是三个不同的平面,有下列命题:
① ②若则
③则 ④直线,直线,那么
⑤若,则 ⑥若,则,
其中正确的说法为__________(填序号)
15.已知,若在内单调,则 的取值范围是
16.已知向量满足,,则的取值范围是_________.
四.解答题:本大题共5小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤。
17.(本题满分10分)已知复数z=a+i(a>0,a∈R),i为虚数单位,且复数为实数.
(1)求复数z ;
(2)在复平面内,若复数(m+z)2对应的点在第一象限,求实数m的取值范围.
18.(本题满分12分)已知.
(1)求的值;
(2)若,且,求的值.
19.(本题满分12分) 如图1,平面五边形中,,,,,是边长为2正三角形.现将沿折起,得到四棱锥(如图2),且.
(1)求证:;
(2)在棱上是否存在点,使得平面?若存在,求的值;若不存在,请说明理由.
20.(本题满分12分)已知函数.
(Ⅰ)求函数在的单调递减区间;
(Ⅱ)在中,内角,,,的对边分别为,,,已知,·=4且D是边BC的中点,AD=,求的周长.
21.(本题满分12分)已知函数.其图象的一个对称中心是,将的图象向左平移个单位长度后得到函数的图象.
(1)求函数的解析式;
(2)若对任意,当时,都有,求实数的最大值.
22.(本题满分12分)如图,正三棱柱的棱长均为2,M是侧棱的中点.
(1)在图中作出平面与平面的交线l(简要说明),并证明平面;
(2)求C点到平面的距离.
本溪县高中2020-2021学年高一下学期6月月考
数学试卷答案
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.C 2.B 3.D 4.B 5.A 6.C 7.D 8.B
二、多项选择题:本大题共4小题,每小题5分,共20分.全对得5分,少选得3分,多选、错选不得分.
9. ABD 10.ABD 11.AD. 12.BD
三.填空题:本大题共4小题,每小题5分,共20分.
13. 14.①⑥ 15. . 16.
四.解答题:本大题共5小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤。
17.(本题满分10分)
【解析】(1)因为z=a+i(a>0),所以z+=a+i+
=a+i+=a+i+=,
由于复数z+为实数,所以1-=0,
因为a>0,解得a=1,因此,z=1+i. 5分
(2)由题意(m+z)2=(m+1+i)2=(m+1)2-1+2(m+1)i=(m2+2m)+2(m+1)i,
由于复数(m+z)2对应的点在第一象限,则,解得m>0.
因此,实数m的取值范围是(0,+∞). 10分
18. (本题满分12分)
解:(1)∵,∴,解得.
∴; 6分
(2)∵,且∴
∴,
∴,∴.∴.
∴,
又∵, ∴. 12分
19. (本题满分12分)
【详解】(1)证明:由已知得,,因为,
所以平面. 又因为,所以 因为平面ADE
5分
(2)在棱上存在点,使得平面, 此时. 6分
理由如下:假设存在点为的中点,设的中点为,连接,,
则,. 因为,且,
所以,且,
所以四边形是平行四边形,
所以. 因为平面,
且平面,所以平面.
所以在棱上存在点,使得平面,
此时. 12分
20.(本题满分12分)
解(1)由已知得 …………3分
又
函数在的单调递减区间为和. …………6分
(2)由(1)知中, A∈(0,π),
又,即 …………9分
由·=4,得bccos A=4,∴bc=8 ①, ∵=(+),∴=(+2·+),
∴7=c2+2bc·cos+b2 ②, 由① ②得:
所以周长为
21. (本题满分12分)
【详解】(1)由题意,得,解得,
又,∴,∴,
从而. 5分
(2)对任意,,且,
,
即在上单调递增,,
由,得,
即的单调增区间为,
由于,
∴当时,,从而,
∴实数t的最大值为. 12分
22. (本题满分12分)
【详解】(1)延长,交CA的延长线于N,连接BN,
N在直线CA上,平面ABC,平面ABC,
又平面ABC内,∴直线平面ABC,
直线C1M,直线C1M?平面MBC1,平面MBC1,
又平面MBC1,∴直线平面MBC1,
平面,平面;
为AA1的中点,CC1AA1,,
,又∵正三棱柱ABC-A1B1C1各棱长均为2,
,C,B,N在以A为圆心半径为2的圆周上,直径为CN,
由于直径所对的圆周角为直角,为直角, 即NB⊥BC,
又∵正三棱柱的侧棱BB1⊥底面ABC,直线平面ABC,∴BB1⊥直线BN,
又∵BB1∩BC=B,平面BB1C1C,平面BB1C1C,∴直线BN⊥平面BB1C1C,
即直线l⊥平面BB1C1C. 7分
(2)由(1)知平面,平面,所以,
,,
所以,
,
设到平面的距离为h,因为,所以,
即 解得,点C到平面的距离为. 12分
同课章节目录
