人教版九年级数学下册27.2.2 相似三角形的判定 课件(22张)
文档属性
| 名称 | 人教版九年级数学下册27.2.2 相似三角形的判定 课件(22张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 425.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 00:00:00 | ||
图片预览




文档简介
BY YUSHEN
相似三角形的判定
DETERMINATION OF SIMILAR TRIANGLE
第二十七章 27.2.2
(平行线分线段成比例)
BY YUSHEN
学习目标
1、了解相似三角形的基础。
2、了解平行线分线段成比例定理推论过程。
3、运用平行线分线段成比例定理进行三角形相似证明及计算。
01
重点
平行线分线段成比例定理和推论及其应用。
02
难点
运用平行线分线段成比例定理进行三角形相似证明及计算。
03
目录
BY YUSHEN
1、了解相似三角形的基础。
2、了解平行线分线段成比例定理推论过程。
3、运用平行线分线段成比例定理进行三角形相似证明及计算。
学习目标
LEARNING OBJECTIVES
01
BY YUSHEN
相似多边形知识点回顾
01
相似多边形概念:
相似多边形特征:
若两个边数相同的多边形,它们的对应角相等、对应边成比例,则这两个多边形叫做相似多边形。
对应角相等、对应边成比例
A
E
D
C
B
A’
B’
C’
D’
E’
若下面两个五边形相似,你知道它们的角和边有什么关系?
∠A=∠A’, ∠B=∠B’, ∠C=∠C’, ∠D=∠D’, ∠E=∠E’
ABA′B′= BCB′C′= CDC′D′= DED′E′= AEA′E′
?
相似比概念:
相似多边形对应边的比
BY YUSHEN
相似三角形
01
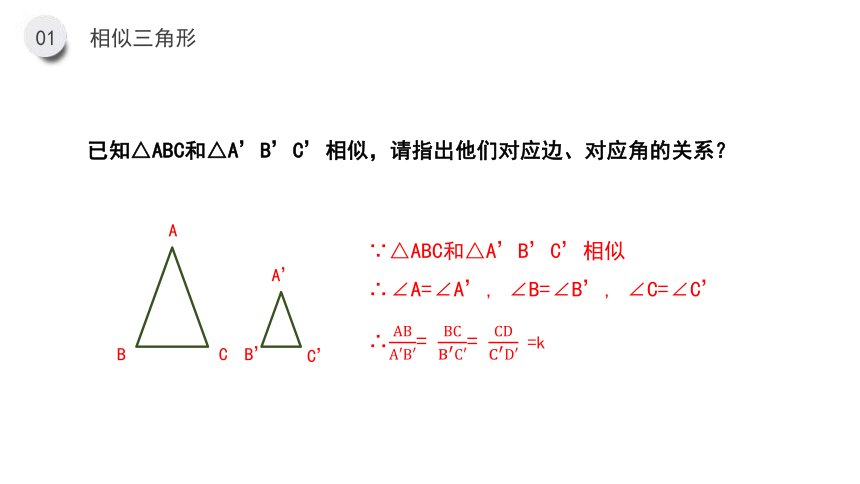
已知△ABC和△A’B’C’相似,请指出他们对应边、对应角的关系?
A
C
B
A’
B’
C’
∵△ABC和△A’B’C’相似
∴∠A=∠A’, ∠B=∠B’, ∠C=∠C’
∴ABA′B′= BCB′C′= CDC′D′ =k
?
BY YUSHEN
判定三角形相似的条件
01
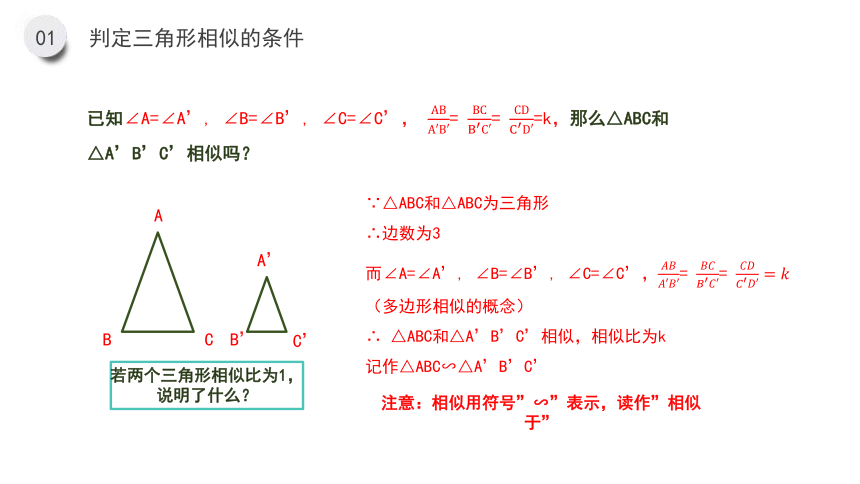
已知∠A=∠A’, ∠B=∠B’, ∠C=∠C’, ABA′B′= BCB′C′= CDC′D′=k,那么△ABC和△A’B’C’相似吗?
?
A
C
B
A’
B’
C’
∵△ABC和△ABC为三角形
∴边数为3
而∠A=∠A’, ∠B=∠B’, ∠C=∠C’,????????????′????′= ????????????′????′= ????????????′????′=????
(多边形相似的概念)
∴ △ABC和△A’B’C’相似,相似比为k
记作△ABC∽△A’B’C’
?
注意:相似用符号”∽”表示,读作”相似于”
若两个三角形相似比为1,
说明了什么?
BY YUSHEN
观察与思考
01
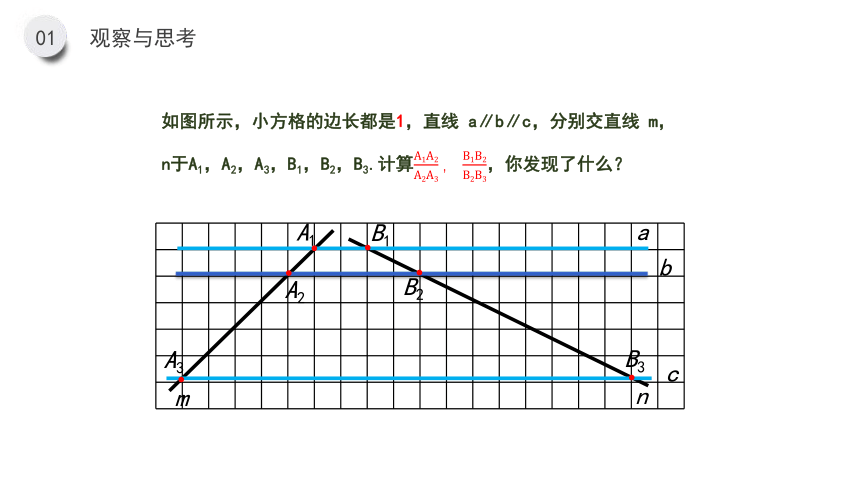
如图所示,小方格的边长都是1,直线 a∥b∥c,分别交直线 m,n于A1,A2,A3,B1,B2,B3.计算A1A2A2A3,B1B2B2B3,你发现了什么?
?
A1
A2
A3
B1
B2
B3
m
n
a
b
c
BY YUSHEN
观察与思考
01
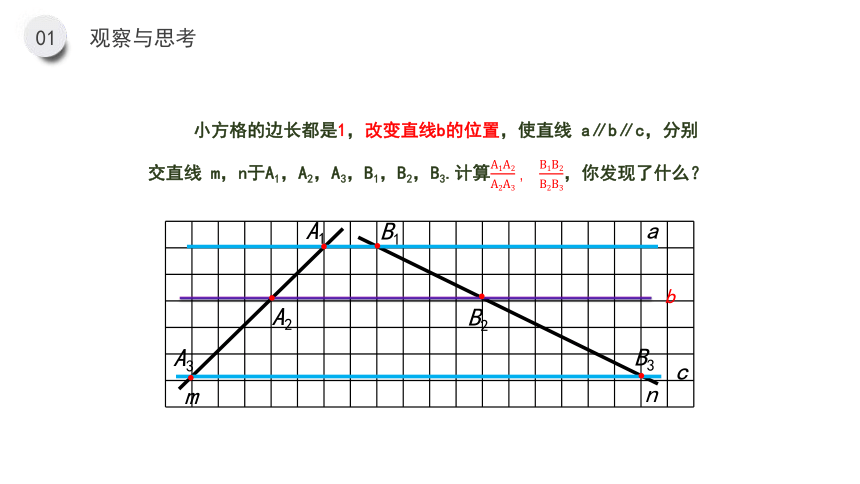
小方格的边长都是1,改变直线b的位置,使直线 a∥b∥c,分别交直线 m,n于A1,A2,A3,B1,B2,B3.计算A1A2A2A3,B1B2B2B3,你发现了什么?
?
A1
A2
A3
B1
B2
B3
m
n
a
b
c
BY YUSHEN
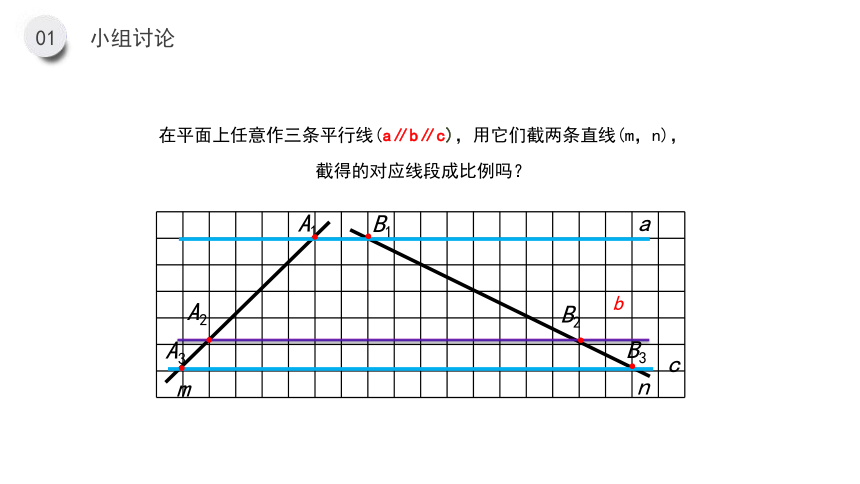
小组讨论
01
在平面上任意作三条平行线(a∥b∥c),用它们截两条直线(m,n),截得的对应线段成比例吗?
A1
A3
B1
B3
m
n
a
b
c
A2
B2
BY YUSHEN
小结
01
一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例。
A1
A2
A3
B1
B2
B3
b
c
a
几何语言:
若a∥b∥c
则 A1A2A2A3?=B1B2B2B3,A1A2A1A3?=B1B2B1B3
???????A2A3A1A2?=B2B3B1B2,A1A3A1A2?=B1B3B1B2 等
?
m
n
BY YUSHEN
观察与思考
01
m
n
A1
A2
A3
B1
B2
B3
b
c
a
A1
A2
A3
B2
B3
b
c
m
n
a
A1
A2
A3
B1
B3
b
c
m
n
a
a∥b∥c
平行于三角形第三边的直线
截其它两边
平行于三角形第三边的直线
截两边的延长线
移动线段n,你发现了什么?
BY YUSHEN
归纳小结
01
A1
A2
A3
B2
B3
b
c
a
A4
A5
A6
B7
B8
a∥b∥c
小结:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
BY YUSHEN
1、了解相似三角形的基础。
2、了解平行线分线段成比例定理推论过程。
3、运用平行线分线段成比例定理进行三角形相似证明及计算。
练一练
HOMEWORK PRACTICE
02
BY YUSHEN
练一练
02
如图,在△ABC中, EF∥BC.
1)如果E、F分别是AB和AC上的点,AE=BE=8,FC=5 ,那么AF的长是多少?
2)如果AB=12,AE=6,AF=6,那么FC的长是多少?
A
B
C
E
F
解:∵ EF∥BC
∴ AEBE?=AFFC
而AE=BE=8,FC=5
∴ 88?=AF5 解得AF=5
?
∵ EF∥BC
∴ AEAB?=AFAC
而AB=12,AE=6,AF=6
∴ 612?=6AC 解得AC=12
FC= AC – AF =6
?
BY YUSHEN
练一练
02
如图,在△ABC中,DE//BC,且DE分别交AB,AC于点D,E,△ADE与△ABC有什么关系?
解:∵ DE∥BC
∴ ADAB?=AEEC??,∠ADE=∠B,∠AED=∠ACB
?
你还记得两个三角形相似的条件吗?
如何证明:ADAB?=AEAC =DEBC
?
F
BY YUSHEN
练一练
02
F
过E点做AB边平行线,与BC边交于点F
∵ DE∥BC, EF∥AB
∴ ADAB?=AEAC , AEAC =BFBC
∵ 四边形BDEF是平行四边形
∴ DE=BF
∴ AEAC =DEBC
∴ AEAC =DEBC= ADAB?而∠ADE=∠B,∠AED=∠ACB ,∠A=∠A
则△ADE∽△ABC
?
BY YUSHEN
判定三角形相似定理
02
平行于三角形一边的直线与其它两边相交,所构成的三角形与原三角形相似.
【注意】平行第三边的直线与其它两边相交有以下两种情况:
BY YUSHEN
练一练
02
1.下列说法中正确的是( )
A.两个直角三角形相似 B.两个等腰三角形相似
C.两个等边三角形相似 D.两个锐角三角形相似
【详解】
A、30°、60°、90°的直角三角形和45°、45°、90°的直角三角形不相似;
B、两个顶角不同的等腰三角形不相似;
C、正确,因为可以根据有两组角对应相等的两个三角形相似来判定;
D、两个锐角不相等的两个三角形不相似.
故选C.
BY YUSHEN
练一练
02
2.如图,DE∥BC,在下列比例式中,不能成立的是( )
A.ADDB=AEEC???????? B.DEBC =?AEEC C.ABAD =?ACAE D.?DBEC =?ABAC
?
3.在△ABC中,点D、E分别在边AB、AC上,如果AD=1,BD=3,那么由下列条件能够判断DE∥BC的是( )
A.????????????????=13 B.????????????????=14 C.????????????????=13 D.????????????????=14
?
【详解】
如图,∵AD=1,BD=3,∴????????????????=14,
当????????????????=14时,????????????????=????????????????,又∵∠DAE=∠BAC,
∴△ADE∽△ABC,∴∠ADE=∠B,∴DE∥BC,
而根据选项A、B、C的条件都不能推出DE∥BC,
故选D.
?
BY YUSHEN
练一练
02
4.(2019·宣武外国语实验学校初三期中)如图,在△ABC中,DE∥BC,DE分别与AB,AC相交于点D,E,若AD=4,DB=2,则DE:BC的值为( )
A.23 B.12 C.34 D.35
?
【解析】
∵DE∥BC,
∴△ADE∽△ABC,
∴????????????????=????????????????=????????????????+????????=46=23.
故选A.
?
BY YUSHEN
课后回顾
判定三角形相似的条件
01
平行线分线段成
比例定理的推论
02
平行线分线段成比例定理
进行三角形相似证明及计算
03
BY YUSHEN
谢谢各位同学倾听
THANK YOU FOR LISTENING
相似三角形的判定
DETERMINATION OF SIMILAR TRIANGLE
第二十七章 27.2.2
(平行线分线段成比例)
BY YUSHEN
学习目标
1、了解相似三角形的基础。
2、了解平行线分线段成比例定理推论过程。
3、运用平行线分线段成比例定理进行三角形相似证明及计算。
01
重点
平行线分线段成比例定理和推论及其应用。
02
难点
运用平行线分线段成比例定理进行三角形相似证明及计算。
03
目录
BY YUSHEN
1、了解相似三角形的基础。
2、了解平行线分线段成比例定理推论过程。
3、运用平行线分线段成比例定理进行三角形相似证明及计算。
学习目标
LEARNING OBJECTIVES
01
BY YUSHEN
相似多边形知识点回顾
01
相似多边形概念:
相似多边形特征:
若两个边数相同的多边形,它们的对应角相等、对应边成比例,则这两个多边形叫做相似多边形。
对应角相等、对应边成比例
A
E
D
C
B
A’
B’
C’
D’
E’
若下面两个五边形相似,你知道它们的角和边有什么关系?
∠A=∠A’, ∠B=∠B’, ∠C=∠C’, ∠D=∠D’, ∠E=∠E’
ABA′B′= BCB′C′= CDC′D′= DED′E′= AEA′E′
?
相似比概念:
相似多边形对应边的比
BY YUSHEN
相似三角形
01
已知△ABC和△A’B’C’相似,请指出他们对应边、对应角的关系?
A
C
B
A’
B’
C’
∵△ABC和△A’B’C’相似
∴∠A=∠A’, ∠B=∠B’, ∠C=∠C’
∴ABA′B′= BCB′C′= CDC′D′ =k
?
BY YUSHEN
判定三角形相似的条件
01
已知∠A=∠A’, ∠B=∠B’, ∠C=∠C’, ABA′B′= BCB′C′= CDC′D′=k,那么△ABC和△A’B’C’相似吗?
?
A
C
B
A’
B’
C’
∵△ABC和△ABC为三角形
∴边数为3
而∠A=∠A’, ∠B=∠B’, ∠C=∠C’,????????????′????′= ????????????′????′= ????????????′????′=????
(多边形相似的概念)
∴ △ABC和△A’B’C’相似,相似比为k
记作△ABC∽△A’B’C’
?
注意:相似用符号”∽”表示,读作”相似于”
若两个三角形相似比为1,
说明了什么?
BY YUSHEN
观察与思考
01
如图所示,小方格的边长都是1,直线 a∥b∥c,分别交直线 m,n于A1,A2,A3,B1,B2,B3.计算A1A2A2A3,B1B2B2B3,你发现了什么?
?
A1
A2
A3
B1
B2
B3
m
n
a
b
c
BY YUSHEN
观察与思考
01
小方格的边长都是1,改变直线b的位置,使直线 a∥b∥c,分别交直线 m,n于A1,A2,A3,B1,B2,B3.计算A1A2A2A3,B1B2B2B3,你发现了什么?
?
A1
A2
A3
B1
B2
B3
m
n
a
b
c
BY YUSHEN
小组讨论
01
在平面上任意作三条平行线(a∥b∥c),用它们截两条直线(m,n),截得的对应线段成比例吗?
A1
A3
B1
B3
m
n
a
b
c
A2
B2
BY YUSHEN
小结
01
一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例。
A1
A2
A3
B1
B2
B3
b
c
a
几何语言:
若a∥b∥c
则 A1A2A2A3?=B1B2B2B3,A1A2A1A3?=B1B2B1B3
???????A2A3A1A2?=B2B3B1B2,A1A3A1A2?=B1B3B1B2 等
?
m
n
BY YUSHEN
观察与思考
01
m
n
A1
A2
A3
B1
B2
B3
b
c
a
A1
A2
A3
B2
B3
b
c
m
n
a
A1
A2
A3
B1
B3
b
c
m
n
a
a∥b∥c
平行于三角形第三边的直线
截其它两边
平行于三角形第三边的直线
截两边的延长线
移动线段n,你发现了什么?
BY YUSHEN
归纳小结
01
A1
A2
A3
B2
B3
b
c
a
A4
A5
A6
B7
B8
a∥b∥c
小结:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
BY YUSHEN
1、了解相似三角形的基础。
2、了解平行线分线段成比例定理推论过程。
3、运用平行线分线段成比例定理进行三角形相似证明及计算。
练一练
HOMEWORK PRACTICE
02
BY YUSHEN
练一练
02
如图,在△ABC中, EF∥BC.
1)如果E、F分别是AB和AC上的点,AE=BE=8,FC=5 ,那么AF的长是多少?
2)如果AB=12,AE=6,AF=6,那么FC的长是多少?
A
B
C
E
F
解:∵ EF∥BC
∴ AEBE?=AFFC
而AE=BE=8,FC=5
∴ 88?=AF5 解得AF=5
?
∵ EF∥BC
∴ AEAB?=AFAC
而AB=12,AE=6,AF=6
∴ 612?=6AC 解得AC=12
FC= AC – AF =6
?
BY YUSHEN
练一练
02
如图,在△ABC中,DE//BC,且DE分别交AB,AC于点D,E,△ADE与△ABC有什么关系?
解:∵ DE∥BC
∴ ADAB?=AEEC??,∠ADE=∠B,∠AED=∠ACB
?
你还记得两个三角形相似的条件吗?
如何证明:ADAB?=AEAC =DEBC
?
F
BY YUSHEN
练一练
02
F
过E点做AB边平行线,与BC边交于点F
∵ DE∥BC, EF∥AB
∴ ADAB?=AEAC , AEAC =BFBC
∵ 四边形BDEF是平行四边形
∴ DE=BF
∴ AEAC =DEBC
∴ AEAC =DEBC= ADAB?而∠ADE=∠B,∠AED=∠ACB ,∠A=∠A
则△ADE∽△ABC
?
BY YUSHEN
判定三角形相似定理
02
平行于三角形一边的直线与其它两边相交,所构成的三角形与原三角形相似.
【注意】平行第三边的直线与其它两边相交有以下两种情况:
BY YUSHEN
练一练
02
1.下列说法中正确的是( )
A.两个直角三角形相似 B.两个等腰三角形相似
C.两个等边三角形相似 D.两个锐角三角形相似
【详解】
A、30°、60°、90°的直角三角形和45°、45°、90°的直角三角形不相似;
B、两个顶角不同的等腰三角形不相似;
C、正确,因为可以根据有两组角对应相等的两个三角形相似来判定;
D、两个锐角不相等的两个三角形不相似.
故选C.
BY YUSHEN
练一练
02
2.如图,DE∥BC,在下列比例式中,不能成立的是( )
A.ADDB=AEEC???????? B.DEBC =?AEEC C.ABAD =?ACAE D.?DBEC =?ABAC
?
3.在△ABC中,点D、E分别在边AB、AC上,如果AD=1,BD=3,那么由下列条件能够判断DE∥BC的是( )
A.????????????????=13 B.????????????????=14 C.????????????????=13 D.????????????????=14
?
【详解】
如图,∵AD=1,BD=3,∴????????????????=14,
当????????????????=14时,????????????????=????????????????,又∵∠DAE=∠BAC,
∴△ADE∽△ABC,∴∠ADE=∠B,∴DE∥BC,
而根据选项A、B、C的条件都不能推出DE∥BC,
故选D.
?
BY YUSHEN
练一练
02
4.(2019·宣武外国语实验学校初三期中)如图,在△ABC中,DE∥BC,DE分别与AB,AC相交于点D,E,若AD=4,DB=2,则DE:BC的值为( )
A.23 B.12 C.34 D.35
?
【解析】
∵DE∥BC,
∴△ADE∽△ABC,
∴????????????????=????????????????=????????????????+????????=46=23.
故选A.
?
BY YUSHEN
课后回顾
判定三角形相似的条件
01
平行线分线段成
比例定理的推论
02
平行线分线段成比例定理
进行三角形相似证明及计算
03
BY YUSHEN
谢谢各位同学倾听
THANK YOU FOR LISTENING
