直线与平面、平面与平面平行的性质
文档属性
| 名称 | 直线与平面、平面与平面平行的性质 |  | |
| 格式 | zip | ||
| 文件大小 | 118.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-18 15:06:22 | ||
图片预览






文档简介
(共27张PPT)
直线与平面、平面与平面平行的性质
请同学们做好课前准备
一、教学目标:
1、知识与技能
(1)掌握直线与平面平行的性质定理及其应用;
(2)掌握两个平面平行的性质定理及其应用。
2、过程与方法
学生通过观察与类比,借助实物模型理解性质
及应用。
3、情感、态度与价值观
(1)进一步提高学生空间想象能力、思维能力;
(2)进一步体会类比的作用;
(3)进一步渗透等价转化的思想。
二、教学重点、难点
重点:两个性质定理 。
难点:(1)性质定理的证明;
(2)性质定理的正确运用。
三、学法与教学用具
1、学法:学生借助实物,通过类比、交流等,得出性质及基本应用。
2、教学用具:投影仪、投影片、长方体模型
四、讲授新课
(一)创设情景、引入新课
1.直线与平面平行的判定定理是什么?
定理 若平面外一条直线与此平面内的一条直线平
行,则该直线与此平面平行.
2.直线与平面平行的判定定理解决了直线与平面平
行的条件问题,反之,在直线与平面平行的条件
下,可以得到什么结论呢?
探究1.如果一条直线与平面平行,那么这条直线
是否与这个平面内的所有直线都平行?
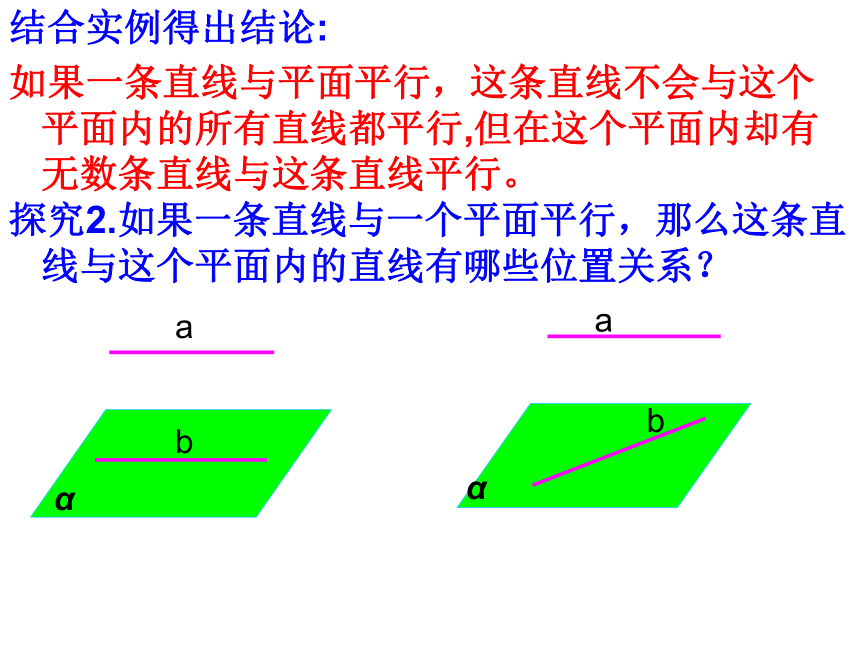
结合实例得出结论:
如果一条直线与平面平行,这条直线不会与这个平面内的所有直线都平行,但在这个平面内却有无数条直线与这条直线平行。
探究2.如果一条直线与一个平面平行,那么这条直线与这个平面内的直线有哪些位置关系?
a
b
α
a
α
b
答:由直线与平面平行的定义,如果一条直线a与
平面α平行,那么a与平面α无公共点,即a上的
点都不在平面α内,平面α内的任何直线与a都
无公共点,这样,平面α内的直线与平面α外的
直线a只能是异面直线或平行直线。
探究3.如果一条直线a与平面α平行,在什么条件下
直线a与平面α内的直线平行呢?
答:由于a与平面α内的任何直线无公共点,所以
过直线a的某一平面,若与平面α相交,则直线a
就平行于这条交线。
探研新知
已知:如图,a∥α,a β,α∩β=b。
求证:a∥b。
证明:∵α∩β=b,∴b α
∵ a∥α,∴a与b无公共点, ∵a β,b β,∴a∥b。
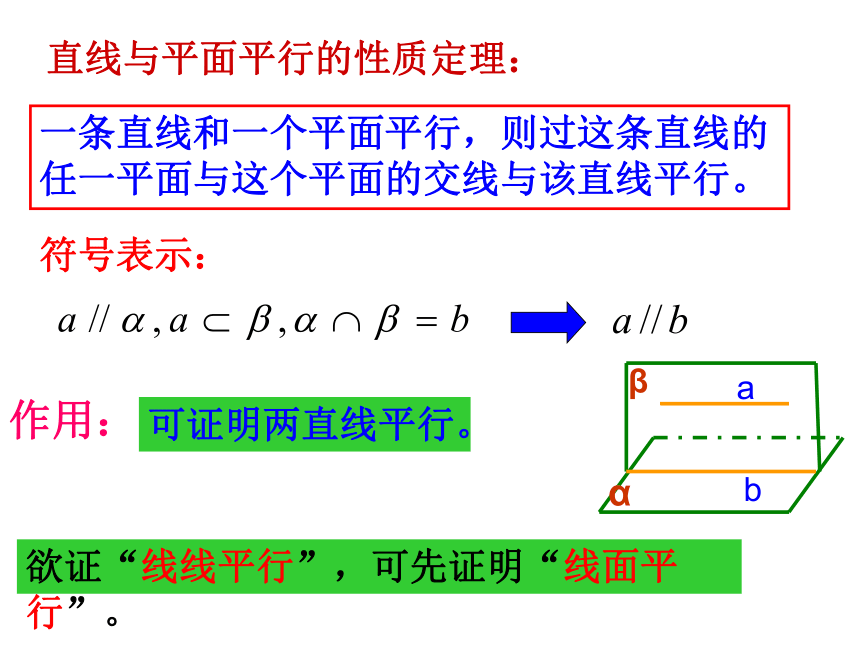
直线与平面平行的性质定理:
一条直线和一个平面平行,则过这条直线的任一平面与这个平面的交线与该直线平行。
a
b
α
β
符号表示:
作用:
可证明两直线平行。
欲证“线线平行”,可先证明“线面平行”。
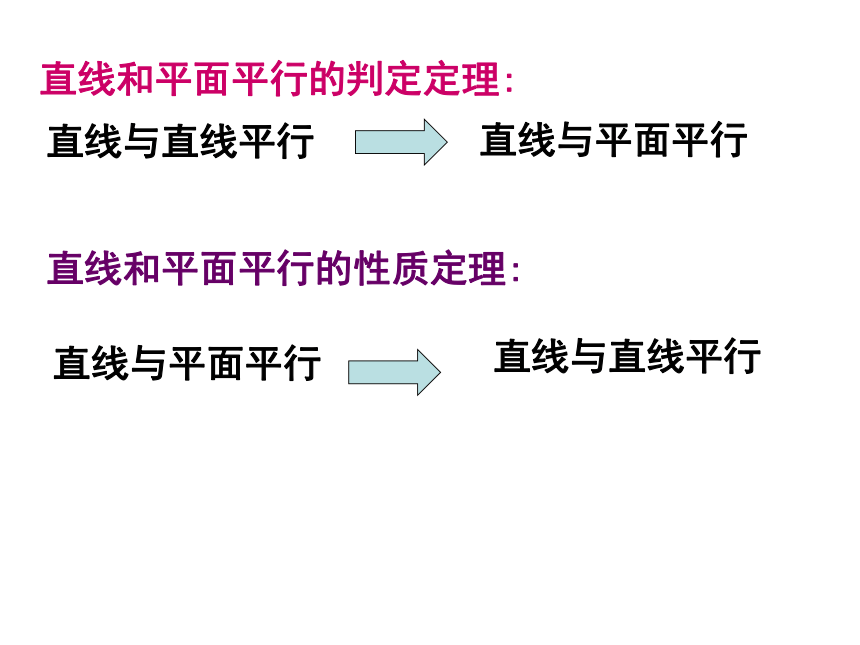
直线和平面平行的判定定理:
直线与直线平行
直线与平面平行
直线和平面平行的性质定理:
直线与直线平行
直线与平面平行
例题示范
例1:已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面。
第一步:将原题改写成数学符号语言
如图,已知直线a,b,平面α,且a//b,a//α,a,b都在平面α外.求证:b//α.
第二步:分析:怎样进行平行的转化?→如何作辅助平面?
第三步:书写证明过程
例题示范
如图,已知直线a,b,平面α,且a//b,a//α,a,b都在平面α外.求证:b//α.
证明:过a作平面β,使它与平面α相交,交线为c.
因为a//α,a β,α ∩β=c,所以 a// c.
因为a//b,所以,b//c.
又因为c α, b α,
所以 b// α。
练习1.一条直线和两个相交平面平行,求证:它和这两个平面的交线平行。
已知直线a∥平面α,直线a∥平面β,平面α∩平面β=b,求证a//b.
问题提出
1.平面与平面平行的判定定理是什么?
2.平面与平面平行的判定定理解决了平面与平面平行的条件问题,反之,在平面与平面平行的条件下,可以得到什么结论呢?
定理 如果一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
β
α
3. 讨论:两个平面平行,那么一个平面内的直线与另一个平面内的直线有什么关系?
l
β
α
4.当第三个平面和两个平行平面都相交,两条交线有什么关系?为什么?
b
a
定理:两个平行平面同时和第三个平面相交,那么它们的交线平行.
定理:两个平行平面同时和第三个
平面相交,那么它们的交线平行.
符号语言:
b
a
例2:夹在两平行平面间的两条平行线段相等.
A
D
B
C
已知:
, AB ∥ CD,且A∈α,C∈α,
B∈β,D∈β.
求证:AB=CD
证明:
∴AB,CD确定一个平面ABDC
∴四边形ABCD是平行四边形
∴ AB=CD
2. 若 ∥ , ∥ ,求证: ∥ .
练习
2. 若 ∥ , ∥ ,求证: ∥ .
练习
a
b
2. 若 ∥ , ∥ ,求证: ∥ .
练习
a
b
b'
a'
2. 若 ∥ , ∥ ,求证: ∥ .
练习
a
b
b'
a'
an
bn
小结(一)
如果不在一个平面内的一条直线和平面内的
一条直线平行,那么这条直线和这个平面平行。
线线平行 线面平行
线面平行 线线平行
线面平行的判定定理
线面平行的性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
小结(二)
如果一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
线线平行 面面平行
面面平行 线线平行
面面平行的判定定理
线面平行的性质定理
两个平行平面同时和第三个平面相交,那么它们的交线平行.
线线平行
线面平行
面面平行
相互转化:
线线平行
线面平行
面面平行
作业:
P61练习,习题2.2A组:1,2, 3。
P62习题2.2A组:4,5,6.
P63习题2.2B组:1,2,3。
谢谢指导
直线与平面、平面与平面平行的性质
请同学们做好课前准备
一、教学目标:
1、知识与技能
(1)掌握直线与平面平行的性质定理及其应用;
(2)掌握两个平面平行的性质定理及其应用。
2、过程与方法
学生通过观察与类比,借助实物模型理解性质
及应用。
3、情感、态度与价值观
(1)进一步提高学生空间想象能力、思维能力;
(2)进一步体会类比的作用;
(3)进一步渗透等价转化的思想。
二、教学重点、难点
重点:两个性质定理 。
难点:(1)性质定理的证明;
(2)性质定理的正确运用。
三、学法与教学用具
1、学法:学生借助实物,通过类比、交流等,得出性质及基本应用。
2、教学用具:投影仪、投影片、长方体模型
四、讲授新课
(一)创设情景、引入新课
1.直线与平面平行的判定定理是什么?
定理 若平面外一条直线与此平面内的一条直线平
行,则该直线与此平面平行.
2.直线与平面平行的判定定理解决了直线与平面平
行的条件问题,反之,在直线与平面平行的条件
下,可以得到什么结论呢?
探究1.如果一条直线与平面平行,那么这条直线
是否与这个平面内的所有直线都平行?
结合实例得出结论:
如果一条直线与平面平行,这条直线不会与这个平面内的所有直线都平行,但在这个平面内却有无数条直线与这条直线平行。
探究2.如果一条直线与一个平面平行,那么这条直线与这个平面内的直线有哪些位置关系?
a
b
α
a
α
b
答:由直线与平面平行的定义,如果一条直线a与
平面α平行,那么a与平面α无公共点,即a上的
点都不在平面α内,平面α内的任何直线与a都
无公共点,这样,平面α内的直线与平面α外的
直线a只能是异面直线或平行直线。
探究3.如果一条直线a与平面α平行,在什么条件下
直线a与平面α内的直线平行呢?
答:由于a与平面α内的任何直线无公共点,所以
过直线a的某一平面,若与平面α相交,则直线a
就平行于这条交线。
探研新知
已知:如图,a∥α,a β,α∩β=b。
求证:a∥b。
证明:∵α∩β=b,∴b α
∵ a∥α,∴a与b无公共点, ∵a β,b β,∴a∥b。
直线与平面平行的性质定理:
一条直线和一个平面平行,则过这条直线的任一平面与这个平面的交线与该直线平行。
a
b
α
β
符号表示:
作用:
可证明两直线平行。
欲证“线线平行”,可先证明“线面平行”。
直线和平面平行的判定定理:
直线与直线平行
直线与平面平行
直线和平面平行的性质定理:
直线与直线平行
直线与平面平行
例题示范
例1:已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面。
第一步:将原题改写成数学符号语言
如图,已知直线a,b,平面α,且a//b,a//α,a,b都在平面α外.求证:b//α.
第二步:分析:怎样进行平行的转化?→如何作辅助平面?
第三步:书写证明过程
例题示范
如图,已知直线a,b,平面α,且a//b,a//α,a,b都在平面α外.求证:b//α.
证明:过a作平面β,使它与平面α相交,交线为c.
因为a//α,a β,α ∩β=c,所以 a// c.
因为a//b,所以,b//c.
又因为c α, b α,
所以 b// α。
练习1.一条直线和两个相交平面平行,求证:它和这两个平面的交线平行。
已知直线a∥平面α,直线a∥平面β,平面α∩平面β=b,求证a//b.
问题提出
1.平面与平面平行的判定定理是什么?
2.平面与平面平行的判定定理解决了平面与平面平行的条件问题,反之,在平面与平面平行的条件下,可以得到什么结论呢?
定理 如果一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
β
α
3. 讨论:两个平面平行,那么一个平面内的直线与另一个平面内的直线有什么关系?
l
β
α
4.当第三个平面和两个平行平面都相交,两条交线有什么关系?为什么?
b
a
定理:两个平行平面同时和第三个平面相交,那么它们的交线平行.
定理:两个平行平面同时和第三个
平面相交,那么它们的交线平行.
符号语言:
b
a
例2:夹在两平行平面间的两条平行线段相等.
A
D
B
C
已知:
, AB ∥ CD,且A∈α,C∈α,
B∈β,D∈β.
求证:AB=CD
证明:
∴AB,CD确定一个平面ABDC
∴四边形ABCD是平行四边形
∴ AB=CD
2. 若 ∥ , ∥ ,求证: ∥ .
练习
2. 若 ∥ , ∥ ,求证: ∥ .
练习
a
b
2. 若 ∥ , ∥ ,求证: ∥ .
练习
a
b
b'
a'
2. 若 ∥ , ∥ ,求证: ∥ .
练习
a
b
b'
a'
an
bn
小结(一)
如果不在一个平面内的一条直线和平面内的
一条直线平行,那么这条直线和这个平面平行。
线线平行 线面平行
线面平行 线线平行
线面平行的判定定理
线面平行的性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
小结(二)
如果一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
线线平行 面面平行
面面平行 线线平行
面面平行的判定定理
线面平行的性质定理
两个平行平面同时和第三个平面相交,那么它们的交线平行.
线线平行
线面平行
面面平行
相互转化:
线线平行
线面平行
面面平行
作业:
P61练习,习题2.2A组:1,2, 3。
P62习题2.2A组:4,5,6.
P63习题2.2B组:1,2,3。
谢谢指导
