人教版2019 必修一 5.7 三角函数的应用同步练习(含解析)
文档属性
| 名称 | 人教版2019 必修一 5.7 三角函数的应用同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-03 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版2019 必修一 5.7 三角函数的应用同步练习
一、单选题
1.电流强度 (安)随时间 (秒)变化的函数 的图像如图所示,则当 秒时,电流强度是(?? )
A.?10安????????????????????????????????????B.?5安????????????????????????????????????C.? 安????????????????????????????????????D.?-5安
2.如图,某地一天从 6 ~ 14 时的温度变化曲线近似满足函数: ,则中午 12 点时最接近的温度为(?? )
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
3.在一个港口,相邻两次高潮发生的时间相距12h,低潮时水深为9m,高潮时水深为15m.每天潮涨潮落时,该港口水的深度y(m)关于时间t(h)的函数图象可以近似地看成函数y=Asin(ωt+φ)+k的图象,其中0≤t≤24,且t=3时涨潮到一次高潮,则该函数的解析式可以是(?? )
A.??????????B.??????????C.??????????D.?
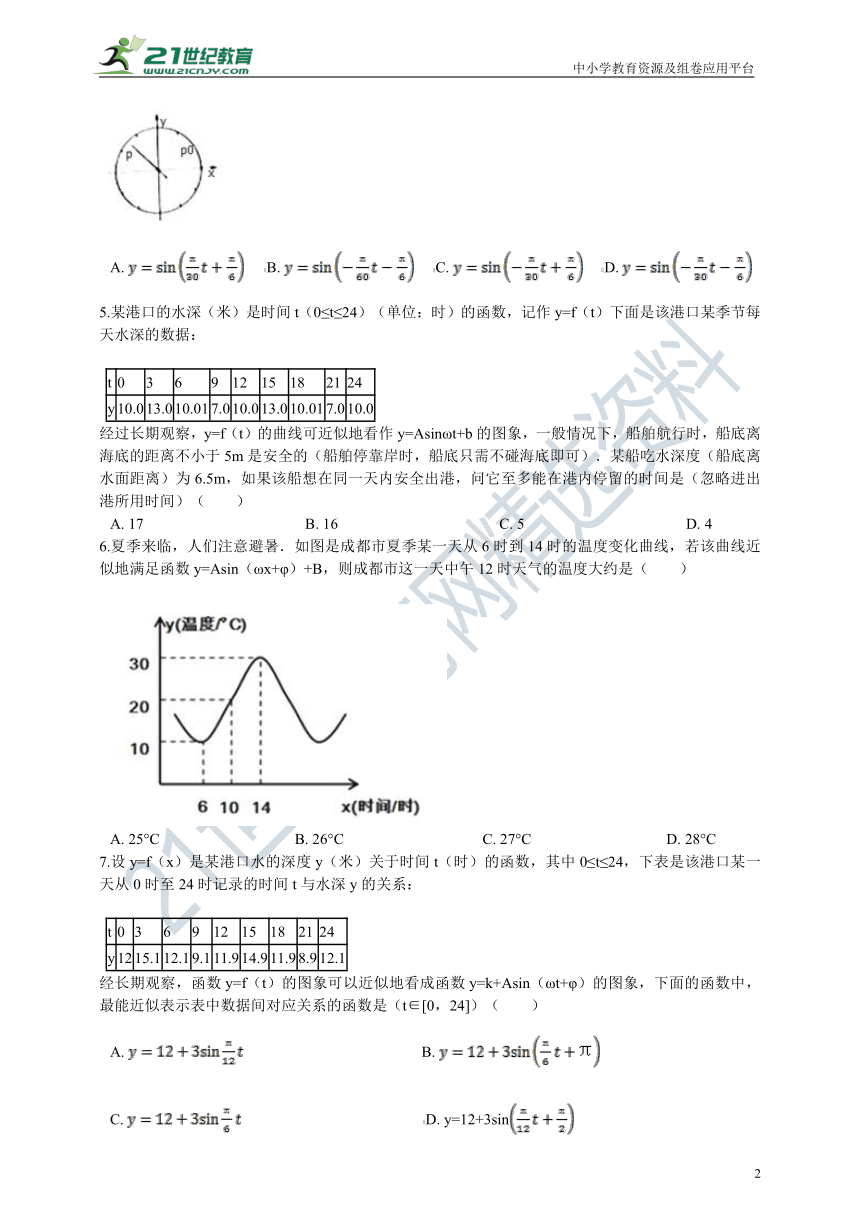
4.为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针指向位置P(x,y),若初如位置为 , 秒针从P0(注:此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t的函数关系为( )
A.??????B.??????C.??????D.?
5.某港口的水深(米)是时间t(0≤t≤24)(单位:时)的函数,记作y=f(t)下面是该港口某季节每天水深的数据:
t 0 3 6 9 12 15 18 21 24
y 10.0 13.0 10.01 7.0 10.0 13.0 10.01 7.0 10.0
经过长期观察,y=f(t)的曲线可近似地看作y=Asinωt+b的图象,一般情况下,船舶航行时,船底离海底的距离不小于5m是安全的(船舶停靠岸时,船底只需不碰海底即可).某船吃水深度(船底离水面距离)为6.5m,如果该船想在同一天内安全出港,问它至多能在港内停留的时间是(忽略进出港所用时间)( )
A.?17??????????????????????????????????????????B.?16??????????????????????????????????????????C.?5??????????????????????????????????????????D.?4
6.夏季来临,人们注意避暑.如图是成都市夏季某一天从6时到14时的温度变化曲线,若该曲线近似地满足函数y=Asin(ωx+φ)+B,则成都市这一天中午12时天气的温度大约是( )
A.?25°C???????????????????????????????????B.?26°C????????????????????????????????????C.?27°C???????????????????????????????????D.?28°C
7.设y=f(x)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24,下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
t 0 3 6 9 12 15 18 21 24
y 12 15.1 12.1 9.1 11.9 14.9 11.9 8.9 12.1
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象,下面的函数中,最能近似表示表中数据间对应关系的函数是(t∈[0,24])( )
A.????????????????????????????????????????????????B.?
C.?????????????????????????????????????????????????D.?y=12+3sin
8.在一个圆形波浪实验水池的中心有三个振动源,假如不计其它因素,在t秒内,它们引发的水面波动可分别由函数 和 描述,如果两个振动源同时启动,则水面波动由两个函数的和表达,在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现的状态是(? )
A.?仍保持平静???????????????????B.?不断波动???????????????????C.?周期性保持平静???????????????????D.?周期性保持波动
9.函数的部分图象如图,则(? )
A.?????????????????B.?????????????????C.?????????????????D.?
10.函数(其中A>0,)的图象如图所示,为了得到f(x)的图象,则只需将g(x)=sin2x的图象(? )
A.?向右平移个长度单位????????????????????????????????????????B.?向左平移个长度单位
C.?向右平移个长度单位????????????????????????????????????????D.?向左平移个长度单位
二、填空题
11.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数 来表示.已知 月份的平均气温最高,为 ℃,12月份的月平均气温最低,为18℃,则10月份的平均气温为________℃.
12.某地一天6时至20时的温度变化近似满足函数y=10sin()+20,(x∈[6,20]),其中x表示时间,y表示温度,设温度不低于20,某人可以进行室外活动,则此人在6时至20时中,可以进行室外活动的时间约为________?小时.
13.国际油价在某一时间内呈现出正弦波动规律:P=Asin(ωπt+ )+60(美元)[t(天),A>0,ω>0],现采集到下列信息:最高油价80美元,当t=150(天)时达到最低油价,则ω=________.
14.某港口在一天24小时内的潮水的高度近似满足关系 ,其中0≤t≤24,S的单位是m,t的单位是h,则18点时潮水起落的速度是________.
三、解答题
15.受日月引力影响,海水会发生涨退潮现象.通常情况下,船在涨潮时驶进港口,退潮时离开港口.某港口在某季节每天港口水位的深度y(米)是时间 ( ,单位:小时, 表示0:00—零时)的函数,其函数关系式为 .已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米.
(1)试求函数 的表达式;
(2)某货船的吃水深度(船底与水面的距离)为7米,安全条例规定船舶航行时船底与海底的距离不小于3.5米是安全的,问该船在当天的什么时间段能够安全进港?若该船欲于当天安全离港,则它最迟应在当天几点以前离开港口?
16.如图,一个半径为4米的筒车按逆时针方向每 分钟转1圈,筒车的轴心O距水面的高度为2米.设筒车上的某个盛水筒W到水面的距离为d(单位:米)(在水面下则d为负数).若以盛水筒W刚浮出水面时开始计算时间,则d与时间t(单位:分钟)之间的关系为 .
(1)求 的值;
(2)求盛水筒W出水后至少经过多少时间就可到达最高点?
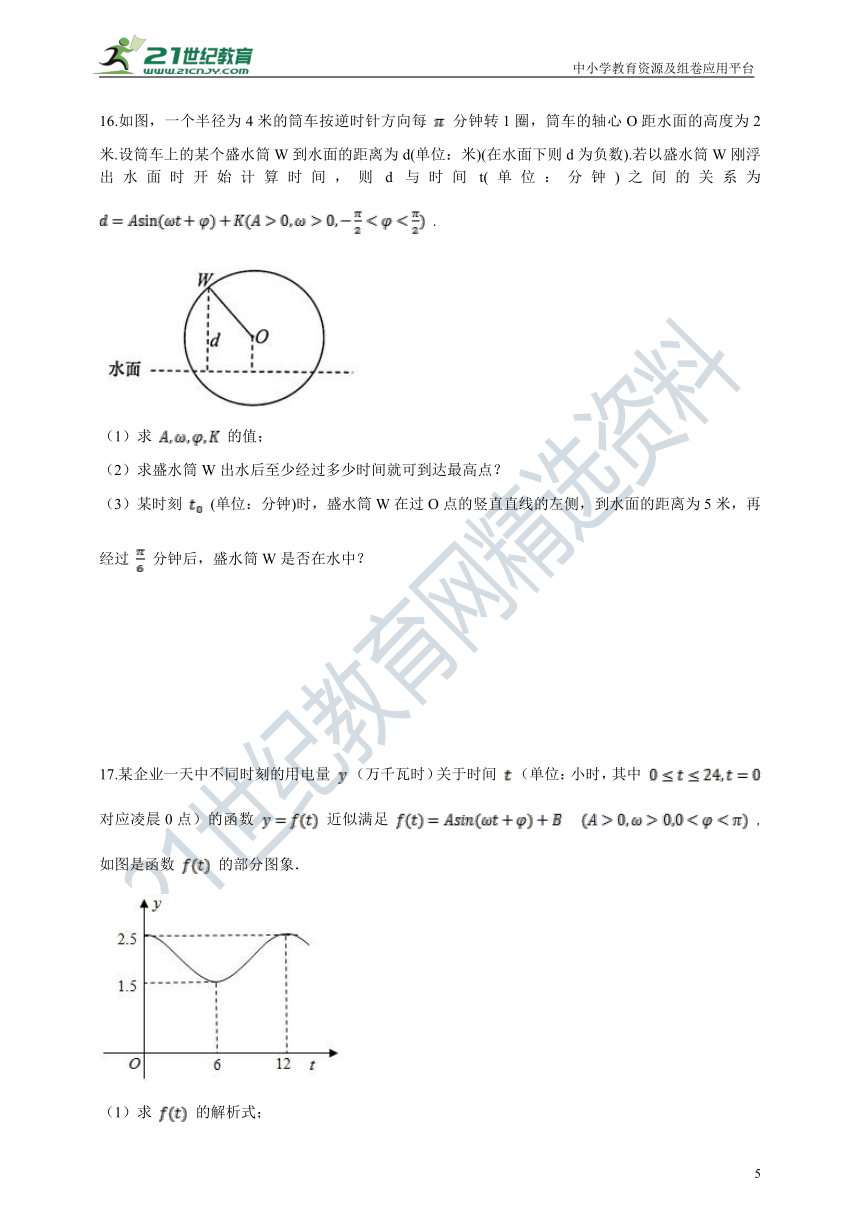
(3)某时刻 (单位:分钟)时,盛水筒W在过O点的竖直直线的左侧,到水面的距离为5米,再经过 分钟后,盛水筒W是否在水中?
17.某企业一天中不同时刻的用电量 (万千瓦时)关于时间 (单位:小时,其中 对应凌晨0点)的函数 近似满足 ? ,如图是函数 的部分图象.
(1)求 的解析式;
(2)已知该企业某天前半日能分配到的供电量 (万千瓦时)与时间 (小时)的关系可用线性函数模型 模拟,当供电量 小于企业用电量 时,企业必须停产.初步预计开始停产的临界时间 在中午11点到12点之间,用二分法估算 所在的一个区间(区间长度精确到15分钟).
18.下表给出的是某港口在某季节每天几个时刻的水深.
时刻 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
水深/m 5.0 8.0 5.0 2.0 5.0 8.0 5.0 2.0 5.0
(1)若该港口的水深y(m)和时刻t(0≤t≤24)的关系可用函数y=Asin(ωt)+b(其中A>0,ω>0,b∈R)来近似描述,求A,ω,b的值;
(2)若一条货船的吃水深度(船底与水面的距离)为4m,安全条例规定至少要有2.5m的安全间隙(船底与海底的距离),试用(1)中的函数关系判断该船何时能进入港口?
19.某实验室白天的温度 (单位: )随时间 (单位: )的变化近似满足函数关系: , .
(1)求实验室白天的最大温差;
(2)若要求实验室温差不高于 ,则在哪段时间实验室需要降温?
20.在一个港口,相邻两次高潮发生时间相距12h,低潮时水的深度为8.4m,高潮时为16m,一次高潮发生在10月10日4:00,每天涨潮落潮时,水的深度d(m)与时间(h)近似满足关系式d=Asin(ωt+φ)+h(A>0,ω>0,|φ|< )
(1)若从10月10日0:00开始计算时间,选用一个三角函数来近似描述该港口的水深d(m)和时间t(h)之间的函数关系.
(2)10月10日17:00该港口水深约为多少?(精确到0.1m)
(3)10月10日这一天该港口共有多长时间水深低于10.3m?
答案解析部分
一、单选题
1.【答案】 D
【解】根据函数图像可知,
,所以解得
由周期公式 代入可得
所以函数
将 代入可得
则
由 可知当 时解得
所以函数
当 时,代入可得
故选:D
【分析】根据所给函数图像,即可求得函数 的解析式,再代入 即可求解.
2.【答案】 B
解:不妨令A>0,B>0,
则由 ?得:A=10,B=20°C;
又 =14﹣6=8,
∴T=16= ,
∴|ω|= ,不妨取ω= .
由图可知,6× +φ=2kπ﹣ (k∈Z),
∴φ=2kπ﹣ ,不妨取φ= .
∴曲线的近似解析式为:y=10sin( x+ )+20,
∴中午12点时最接近的温度为:y=10sin( ×12+ )+20°C=10sin +20°C=20+10sin =5 +20°C≈27°C.
故答案为:B.
3.【答案】A
解:依题意, ,解得 , 又T= ,
∴ω= .
又f(3)=15,
∴3sin( +φ)+12=15,
∴sin( +φ)=1.
∴φ=0,
∴y=f(t)=3sin t+12.
故选:A.
4.【答案】 C
解:∵秒针是顺时针旋转,
∴角速度ω<0.又由每60秒转一周,
∴ω=﹣=﹣(弧度/秒),
由P0( , ),得,cosφ= , sinφ= .
解得φ= ,
故选:C.
5.【答案】 B
解:由已知数据,易知y=f(t)的周期T=12,振幅A=13﹣10=3,b=10,所以;
由该船进出港时,水深应不小于5+6.5=11.5(m),∴+10≥11.5,
即(k∈Z),
∴12k+1≤t≤12k+5(k∈Z),在同一天内,取k=0或1,
所以1≤t≤5或13≤t≤17.
故该船可在当日凌晨1时进港,17时离港,它在港内至多停留16小时.
6.【答案】 C
解:由题意以及函数的图象可知,A+B=30,﹣A+B=10,所以A=10,B=20
∵ , ∴T=16
∵T= , ∴
∴y=10sin(x+φ)+20
∵图象经过点(14,30)
∴30=10sin(×14+φ)+20
∴sin(×14+φ)=1
∴φ可以取
∴y=10sin(x+)+20
当x=12时,y=10sin(×12+)+20=10×+20≈27.07
故选C.
7.【答案】 C
解:由于y=f(t)可以近似看成y=k+Asin(ωx+φ)的图象,根据港口某一天从0时至24时记录的时间t与水深y的关系,可得函数的周期T=12可排除A、D,将(3,15)代入B,C,可排除B,C满足.
故选C
8.【答案】 A
解:∵ +
=sint+sint?cos +cost?sin +sint?cos +cost?sin
=sint﹣ sint+ cost﹣ sint﹣ cost
=sint﹣sint=0
即三个振动源同时开始工作时,水面仍保持平静
故选A
9.【答案】 C
【解】观察图象可知,A=1,T=4(3-1)=8,所以。将(1,1)代入得所以, 故选C。
10.【答案】 B
【【解】观察图象知A=1,T=4()=π,=2,即, 将(, 0)代入上式,得, 结合得=。因此。只需将g(x)=sin2x的图象向左平移个长度单位即得。选B。
二、填空题
11.【答案】 20.5
【解】据题意得 ,
解得 ,
所以
令 得 .
故答案为:20.5
12.【答案】 8
解:由题意,10sin()+20≥20
∴sin()≥0
∴2kπ≤≤2kπ+π
∴16k﹣6≤x≤16k+2,
∵x∈[6,20],
∴10≤x≤18
∴此人在6时至20时中,可以进行室外活动的时间约为18﹣10=8小时
故答案为:8
13.【答案】
【解】因为国际油价在某一时间内呈现出正弦波动规律:P=Asin(ωπt+ )+60(美元)[t(天),A>0,ω>0],最高油价80美元,所以80=Asin(ωπt+ )+60,因为sin(ωπt+ )≤1,所以A=20,
当t=150(天)时达到最低油价,即sin(150ωπ+ )=﹣1,
此时150ωπ+ =2kπ﹣ ,k∈Z,
因为ω>0,所以令k=1,150ωπ+ =2π﹣ ,
解得ω= .
故答案为: .
14.【答案】
【解】由题意,∵
∴v=S'=
当t=18时,速度v=
故答案为
三、解答题
15.【答案】 (1)解:依题意, ,∴ , ,又 ,∴ ,∴ ,又 ,∴ ,∴
(2)解:令 得 ,∴ ,∴
∵ ,∴ 或 ,∴该船当天安全进港的时间为1~5点和13~17点,最迟应在当天的17点以前离开港口
16.【答案】 (1)解:由题意知, ,即 ,所以 ,
由题意半径为4米,筒车的轴心O距水面的高度为2米,可得: ,
当 时, ,代入 得, ,
因为 ,所以
(2)解:由(1)知: ,
盛水筒达到最高点时, ,
当 时, ,所以 ,
所以 ,解得 ,
因为 ,所以,当 时, ,
所以盛水筒出水后至少经过 分钟就可达到最高点
(3)解:由题知: ,即 ,
由题意,盛水筒W在过O点的竖直直线的左侧,知 ,
所以 ,
所以 ,
所以,再经过 分钟后 ,
所以再经过 分钟后盛水筒不在水中
?
17.【答案】 (1)解:由图象可知A= = ,B= =2,T=12= ,ω= , 代入点(0,2.5)得sinφ=1, ∵0<φ<π,∴φ= ;
综上,A= ,B=2,ω= ,φ= ,
即f(t)= sin( t+ )+2.
(2)解:由(1)知f(t)= sin( t+ )+2= cos t+2,
令h(t)=f(t)-g(t),
设h(t0)=0,则t0为该企业的开始停产的临界时间;
易知h(t)在(11,12)上是单调递增函数;
由h(11)=f(11)-g(11)= cos +2+2×11-25= -1<0,
h(12)=f(12)-g(12)= cos +2+2×12-25= >0,
又h(11.5)=f(11.5)-g(11.5)= cos +2+2×11.5-25= cos(- )= cos = >0,
则t0∈(11,11.5),即11点到11点30分之间(大于15分钟),
又h(11.25)=f(11.25)-g(11.25)= cos +2+2×11.25-25< ×1-0.5=0,
则t0∈(11.25,11.5),即11点15分到11点30分之间(正好15分钟).
所以,企业开始停产的临界时间t0所在的区间为(11.25,11.5).
18.【答案】 解:(1)由已知数据,易知y=f(t)的周期T=12,振幅A=3,b=5,所以ω==
(2)由(1)知y=3sin(t)+5(0≤t≤24);
由该船进出港时,水深应不小于4+2.5=6.5(m),
∴当y≥6.5时,货船就可以进港,即3sin(t)+5≥6.5,
∴sin(t)≥0.5,
∵0≤t≤24,∴0≤t≤4π
∴≤t≤ , 或≤t≤ ,
所以1≤t≤5或13≤t≤17.
故该船可在当日凌晨1:00~5:00和13:00~17:00进入港口.
19.【答案】 (1)解:已知 ,
因为 ,所以 , ,
所以 在 上取得最大值为12,取得最小值为9,
故实验室这一天最高温度为 ,最低温度为 ,最大温差为
(2)解:依题意当 时,实验室需要降温,即 ,
,∴ , ,
∴ , ,又∵ ,
∴ ,即在10时到18时实验室需要降温
20.【答案】 (1)解:依题意知T= =12,
故ω= ,h= =12.2,A=16-12.2=3.8,
所以d=3.8sin( t+φ)+12.2
又因为t=4时,d=16,所以sin( t+φ)=1,
所以φ=- ,所以d=3.8sin( t- )+12.2
(2)解:t=17时,d=3.8sin( - )+12.2=3.8sin +12.2≈15.5(m)
(3)解:令3.8sin( t- )+12.2<10.3,即sin( t- )<- ,
因此2kπ+ < t- <2kπ+ ,k∈Z
所以12k+8令k=0,t(8,12),令k=1,t∈(20,24)
故这一天共有8h水深低于10.3m.
2
人教版2019 必修一 5.7 三角函数的应用同步练习
一、单选题
1.电流强度 (安)随时间 (秒)变化的函数 的图像如图所示,则当 秒时,电流强度是(?? )
A.?10安????????????????????????????????????B.?5安????????????????????????????????????C.? 安????????????????????????????????????D.?-5安
2.如图,某地一天从 6 ~ 14 时的温度变化曲线近似满足函数: ,则中午 12 点时最接近的温度为(?? )
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
3.在一个港口,相邻两次高潮发生的时间相距12h,低潮时水深为9m,高潮时水深为15m.每天潮涨潮落时,该港口水的深度y(m)关于时间t(h)的函数图象可以近似地看成函数y=Asin(ωt+φ)+k的图象,其中0≤t≤24,且t=3时涨潮到一次高潮,则该函数的解析式可以是(?? )
A.??????????B.??????????C.??????????D.?
4.为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针指向位置P(x,y),若初如位置为 , 秒针从P0(注:此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t的函数关系为( )
A.??????B.??????C.??????D.?
5.某港口的水深(米)是时间t(0≤t≤24)(单位:时)的函数,记作y=f(t)下面是该港口某季节每天水深的数据:
t 0 3 6 9 12 15 18 21 24
y 10.0 13.0 10.01 7.0 10.0 13.0 10.01 7.0 10.0
经过长期观察,y=f(t)的曲线可近似地看作y=Asinωt+b的图象,一般情况下,船舶航行时,船底离海底的距离不小于5m是安全的(船舶停靠岸时,船底只需不碰海底即可).某船吃水深度(船底离水面距离)为6.5m,如果该船想在同一天内安全出港,问它至多能在港内停留的时间是(忽略进出港所用时间)( )
A.?17??????????????????????????????????????????B.?16??????????????????????????????????????????C.?5??????????????????????????????????????????D.?4
6.夏季来临,人们注意避暑.如图是成都市夏季某一天从6时到14时的温度变化曲线,若该曲线近似地满足函数y=Asin(ωx+φ)+B,则成都市这一天中午12时天气的温度大约是( )
A.?25°C???????????????????????????????????B.?26°C????????????????????????????????????C.?27°C???????????????????????????????????D.?28°C
7.设y=f(x)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24,下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
t 0 3 6 9 12 15 18 21 24
y 12 15.1 12.1 9.1 11.9 14.9 11.9 8.9 12.1
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象,下面的函数中,最能近似表示表中数据间对应关系的函数是(t∈[0,24])( )
A.????????????????????????????????????????????????B.?
C.?????????????????????????????????????????????????D.?y=12+3sin
8.在一个圆形波浪实验水池的中心有三个振动源,假如不计其它因素,在t秒内,它们引发的水面波动可分别由函数 和 描述,如果两个振动源同时启动,则水面波动由两个函数的和表达,在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现的状态是(? )
A.?仍保持平静???????????????????B.?不断波动???????????????????C.?周期性保持平静???????????????????D.?周期性保持波动
9.函数的部分图象如图,则(? )
A.?????????????????B.?????????????????C.?????????????????D.?
10.函数(其中A>0,)的图象如图所示,为了得到f(x)的图象,则只需将g(x)=sin2x的图象(? )
A.?向右平移个长度单位????????????????????????????????????????B.?向左平移个长度单位
C.?向右平移个长度单位????????????????????????????????????????D.?向左平移个长度单位
二、填空题
11.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数 来表示.已知 月份的平均气温最高,为 ℃,12月份的月平均气温最低,为18℃,则10月份的平均气温为________℃.
12.某地一天6时至20时的温度变化近似满足函数y=10sin()+20,(x∈[6,20]),其中x表示时间,y表示温度,设温度不低于20,某人可以进行室外活动,则此人在6时至20时中,可以进行室外活动的时间约为________?小时.
13.国际油价在某一时间内呈现出正弦波动规律:P=Asin(ωπt+ )+60(美元)[t(天),A>0,ω>0],现采集到下列信息:最高油价80美元,当t=150(天)时达到最低油价,则ω=________.
14.某港口在一天24小时内的潮水的高度近似满足关系 ,其中0≤t≤24,S的单位是m,t的单位是h,则18点时潮水起落的速度是________.
三、解答题
15.受日月引力影响,海水会发生涨退潮现象.通常情况下,船在涨潮时驶进港口,退潮时离开港口.某港口在某季节每天港口水位的深度y(米)是时间 ( ,单位:小时, 表示0:00—零时)的函数,其函数关系式为 .已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米.
(1)试求函数 的表达式;
(2)某货船的吃水深度(船底与水面的距离)为7米,安全条例规定船舶航行时船底与海底的距离不小于3.5米是安全的,问该船在当天的什么时间段能够安全进港?若该船欲于当天安全离港,则它最迟应在当天几点以前离开港口?
16.如图,一个半径为4米的筒车按逆时针方向每 分钟转1圈,筒车的轴心O距水面的高度为2米.设筒车上的某个盛水筒W到水面的距离为d(单位:米)(在水面下则d为负数).若以盛水筒W刚浮出水面时开始计算时间,则d与时间t(单位:分钟)之间的关系为 .
(1)求 的值;
(2)求盛水筒W出水后至少经过多少时间就可到达最高点?
(3)某时刻 (单位:分钟)时,盛水筒W在过O点的竖直直线的左侧,到水面的距离为5米,再经过 分钟后,盛水筒W是否在水中?
17.某企业一天中不同时刻的用电量 (万千瓦时)关于时间 (单位:小时,其中 对应凌晨0点)的函数 近似满足 ? ,如图是函数 的部分图象.
(1)求 的解析式;
(2)已知该企业某天前半日能分配到的供电量 (万千瓦时)与时间 (小时)的关系可用线性函数模型 模拟,当供电量 小于企业用电量 时,企业必须停产.初步预计开始停产的临界时间 在中午11点到12点之间,用二分法估算 所在的一个区间(区间长度精确到15分钟).
18.下表给出的是某港口在某季节每天几个时刻的水深.
时刻 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
水深/m 5.0 8.0 5.0 2.0 5.0 8.0 5.0 2.0 5.0
(1)若该港口的水深y(m)和时刻t(0≤t≤24)的关系可用函数y=Asin(ωt)+b(其中A>0,ω>0,b∈R)来近似描述,求A,ω,b的值;
(2)若一条货船的吃水深度(船底与水面的距离)为4m,安全条例规定至少要有2.5m的安全间隙(船底与海底的距离),试用(1)中的函数关系判断该船何时能进入港口?
19.某实验室白天的温度 (单位: )随时间 (单位: )的变化近似满足函数关系: , .
(1)求实验室白天的最大温差;
(2)若要求实验室温差不高于 ,则在哪段时间实验室需要降温?
20.在一个港口,相邻两次高潮发生时间相距12h,低潮时水的深度为8.4m,高潮时为16m,一次高潮发生在10月10日4:00,每天涨潮落潮时,水的深度d(m)与时间(h)近似满足关系式d=Asin(ωt+φ)+h(A>0,ω>0,|φ|< )
(1)若从10月10日0:00开始计算时间,选用一个三角函数来近似描述该港口的水深d(m)和时间t(h)之间的函数关系.
(2)10月10日17:00该港口水深约为多少?(精确到0.1m)
(3)10月10日这一天该港口共有多长时间水深低于10.3m?
答案解析部分
一、单选题
1.【答案】 D
【解】根据函数图像可知,
,所以解得
由周期公式 代入可得
所以函数
将 代入可得
则
由 可知当 时解得
所以函数
当 时,代入可得
故选:D
【分析】根据所给函数图像,即可求得函数 的解析式,再代入 即可求解.
2.【答案】 B
解:不妨令A>0,B>0,
则由 ?得:A=10,B=20°C;
又 =14﹣6=8,
∴T=16= ,
∴|ω|= ,不妨取ω= .
由图可知,6× +φ=2kπ﹣ (k∈Z),
∴φ=2kπ﹣ ,不妨取φ= .
∴曲线的近似解析式为:y=10sin( x+ )+20,
∴中午12点时最接近的温度为:y=10sin( ×12+ )+20°C=10sin +20°C=20+10sin =5 +20°C≈27°C.
故答案为:B.
3.【答案】A
解:依题意, ,解得 , 又T= ,
∴ω= .
又f(3)=15,
∴3sin( +φ)+12=15,
∴sin( +φ)=1.
∴φ=0,
∴y=f(t)=3sin t+12.
故选:A.
4.【答案】 C
解:∵秒针是顺时针旋转,
∴角速度ω<0.又由每60秒转一周,
∴ω=﹣=﹣(弧度/秒),
由P0( , ),得,cosφ= , sinφ= .
解得φ= ,
故选:C.
5.【答案】 B
解:由已知数据,易知y=f(t)的周期T=12,振幅A=13﹣10=3,b=10,所以;
由该船进出港时,水深应不小于5+6.5=11.5(m),∴+10≥11.5,
即(k∈Z),
∴12k+1≤t≤12k+5(k∈Z),在同一天内,取k=0或1,
所以1≤t≤5或13≤t≤17.
故该船可在当日凌晨1时进港,17时离港,它在港内至多停留16小时.
6.【答案】 C
解:由题意以及函数的图象可知,A+B=30,﹣A+B=10,所以A=10,B=20
∵ , ∴T=16
∵T= , ∴
∴y=10sin(x+φ)+20
∵图象经过点(14,30)
∴30=10sin(×14+φ)+20
∴sin(×14+φ)=1
∴φ可以取
∴y=10sin(x+)+20
当x=12时,y=10sin(×12+)+20=10×+20≈27.07
故选C.
7.【答案】 C
解:由于y=f(t)可以近似看成y=k+Asin(ωx+φ)的图象,根据港口某一天从0时至24时记录的时间t与水深y的关系,可得函数的周期T=12可排除A、D,将(3,15)代入B,C,可排除B,C满足.
故选C
8.【答案】 A
解:∵ +
=sint+sint?cos +cost?sin +sint?cos +cost?sin
=sint﹣ sint+ cost﹣ sint﹣ cost
=sint﹣sint=0
即三个振动源同时开始工作时,水面仍保持平静
故选A
9.【答案】 C
【解】观察图象可知,A=1,T=4(3-1)=8,所以。将(1,1)代入得所以, 故选C。
10.【答案】 B
【【解】观察图象知A=1,T=4()=π,=2,即, 将(, 0)代入上式,得, 结合得=。因此。只需将g(x)=sin2x的图象向左平移个长度单位即得。选B。
二、填空题
11.【答案】 20.5
【解】据题意得 ,
解得 ,
所以
令 得 .
故答案为:20.5
12.【答案】 8
解:由题意,10sin()+20≥20
∴sin()≥0
∴2kπ≤≤2kπ+π
∴16k﹣6≤x≤16k+2,
∵x∈[6,20],
∴10≤x≤18
∴此人在6时至20时中,可以进行室外活动的时间约为18﹣10=8小时
故答案为:8
13.【答案】
【解】因为国际油价在某一时间内呈现出正弦波动规律:P=Asin(ωπt+ )+60(美元)[t(天),A>0,ω>0],最高油价80美元,所以80=Asin(ωπt+ )+60,因为sin(ωπt+ )≤1,所以A=20,
当t=150(天)时达到最低油价,即sin(150ωπ+ )=﹣1,
此时150ωπ+ =2kπ﹣ ,k∈Z,
因为ω>0,所以令k=1,150ωπ+ =2π﹣ ,
解得ω= .
故答案为: .
14.【答案】
【解】由题意,∵
∴v=S'=
当t=18时,速度v=
故答案为
三、解答题
15.【答案】 (1)解:依题意, ,∴ , ,又 ,∴ ,∴ ,又 ,∴ ,∴
(2)解:令 得 ,∴ ,∴
∵ ,∴ 或 ,∴该船当天安全进港的时间为1~5点和13~17点,最迟应在当天的17点以前离开港口
16.【答案】 (1)解:由题意知, ,即 ,所以 ,
由题意半径为4米,筒车的轴心O距水面的高度为2米,可得: ,
当 时, ,代入 得, ,
因为 ,所以
(2)解:由(1)知: ,
盛水筒达到最高点时, ,
当 时, ,所以 ,
所以 ,解得 ,
因为 ,所以,当 时, ,
所以盛水筒出水后至少经过 分钟就可达到最高点
(3)解:由题知: ,即 ,
由题意,盛水筒W在过O点的竖直直线的左侧,知 ,
所以 ,
所以 ,
所以,再经过 分钟后 ,
所以再经过 分钟后盛水筒不在水中
?
17.【答案】 (1)解:由图象可知A= = ,B= =2,T=12= ,ω= , 代入点(0,2.5)得sinφ=1, ∵0<φ<π,∴φ= ;
综上,A= ,B=2,ω= ,φ= ,
即f(t)= sin( t+ )+2.
(2)解:由(1)知f(t)= sin( t+ )+2= cos t+2,
令h(t)=f(t)-g(t),
设h(t0)=0,则t0为该企业的开始停产的临界时间;
易知h(t)在(11,12)上是单调递增函数;
由h(11)=f(11)-g(11)= cos +2+2×11-25= -1<0,
h(12)=f(12)-g(12)= cos +2+2×12-25= >0,
又h(11.5)=f(11.5)-g(11.5)= cos +2+2×11.5-25= cos(- )= cos = >0,
则t0∈(11,11.5),即11点到11点30分之间(大于15分钟),
又h(11.25)=f(11.25)-g(11.25)= cos +2+2×11.25-25< ×1-0.5=0,
则t0∈(11.25,11.5),即11点15分到11点30分之间(正好15分钟).
所以,企业开始停产的临界时间t0所在的区间为(11.25,11.5).
18.【答案】 解:(1)由已知数据,易知y=f(t)的周期T=12,振幅A=3,b=5,所以ω==
(2)由(1)知y=3sin(t)+5(0≤t≤24);
由该船进出港时,水深应不小于4+2.5=6.5(m),
∴当y≥6.5时,货船就可以进港,即3sin(t)+5≥6.5,
∴sin(t)≥0.5,
∵0≤t≤24,∴0≤t≤4π
∴≤t≤ , 或≤t≤ ,
所以1≤t≤5或13≤t≤17.
故该船可在当日凌晨1:00~5:00和13:00~17:00进入港口.
19.【答案】 (1)解:已知 ,
因为 ,所以 , ,
所以 在 上取得最大值为12,取得最小值为9,
故实验室这一天最高温度为 ,最低温度为 ,最大温差为
(2)解:依题意当 时,实验室需要降温,即 ,
,∴ , ,
∴ , ,又∵ ,
∴ ,即在10时到18时实验室需要降温
20.【答案】 (1)解:依题意知T= =12,
故ω= ,h= =12.2,A=16-12.2=3.8,
所以d=3.8sin( t+φ)+12.2
又因为t=4时,d=16,所以sin( t+φ)=1,
所以φ=- ,所以d=3.8sin( t- )+12.2
(2)解:t=17时,d=3.8sin( - )+12.2=3.8sin +12.2≈15.5(m)
(3)解:令3.8sin( t- )+12.2<10.3,即sin( t- )<- ,
因此2kπ+ < t- <2kπ+ ,k∈Z
所以12k+8
故这一天共有8h水深低于10.3m.
2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
