相似三角形（-）

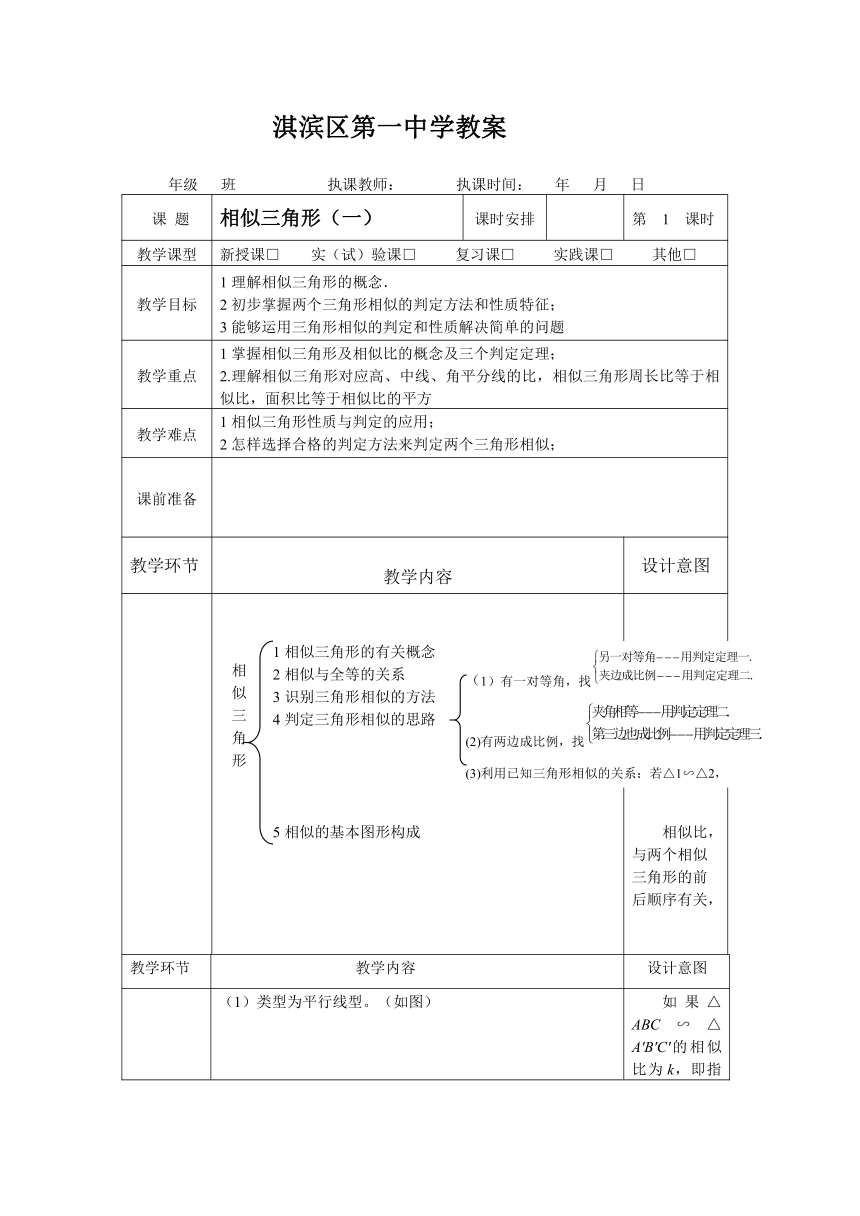
淇滨区第一中学教案
年级 班 执课教师： 执课时间： 年 月 日
课 题 相似三角形（一） 课时安排 第 1 课时
教学课型 新授课□ 实（试）验课□ 复习课□ 实践课□ 其他□
教学目标 1理解相似三角形的概念．2初步掌握两个三角形相似的判定方法和性质特征；3能够运用三角形相似的判定和性质解决简单的问题
教学重点 1掌握相似三角形及相似比的概念及三个判定定理；2.理解相似三角形对应高、中线、角平分线的比，相似三角形周长比等于相似比，面积比等于相似比的平方
教学难点 1相似三角形性质与判定的应用；2怎样选择合格的判定方法来判定两个三角形相似；
课前准备
教学环节 教学内容 设计意图
1相似三角形的有关概念2相似与全等的关系3识别三角形相似的方法4判定三角形相似的思路5相似的基本图形构成 相似比，与两个相似三角形的前后顺序有关，
教学环节 教学内容 设计意图
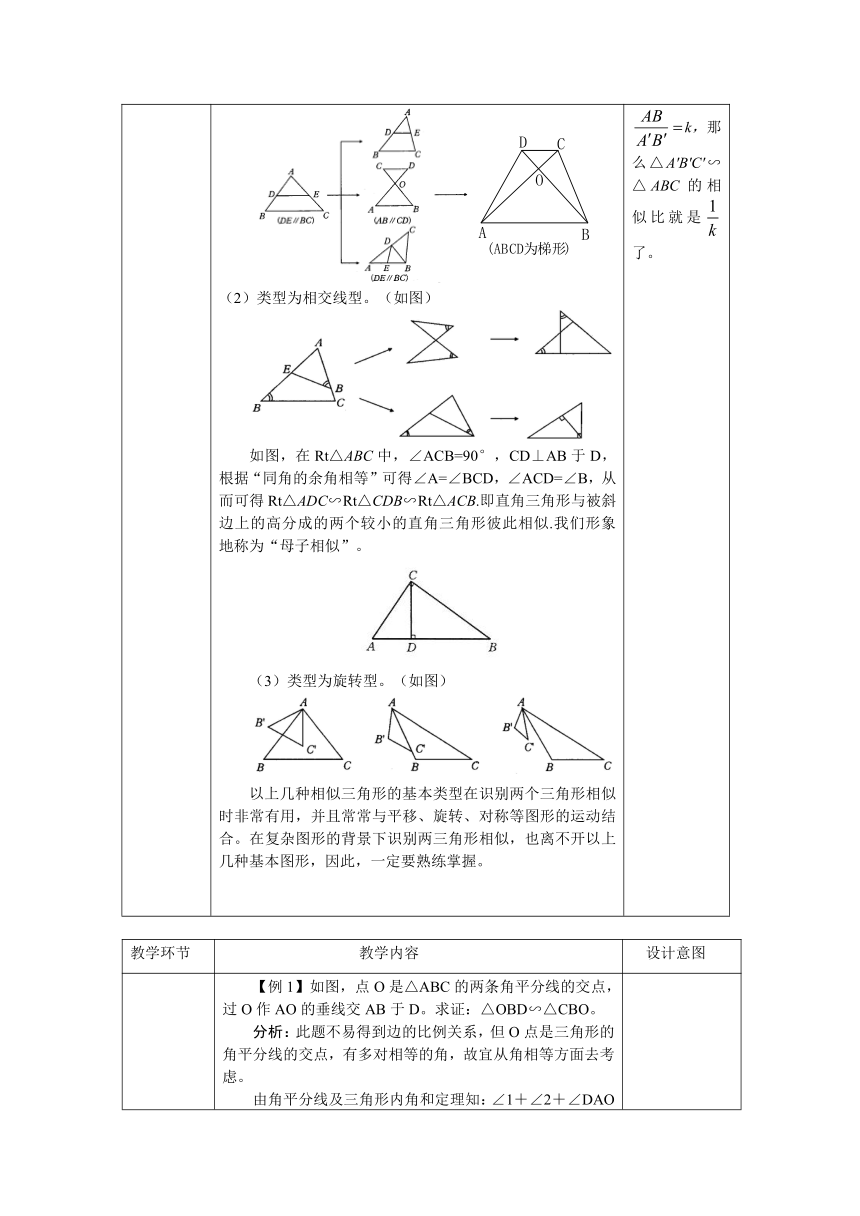
（1）类型为平行线型。（如图）（2）类型为相交线型。（如图）如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，根据“同角的余角相等”可得∠A=∠BCD，∠ACD=∠B，从而可得Rt△ADC∽Rt△CDB∽Rt△ACB.即直角三角形与被斜边上的高分成的两个较小的直角三角形彼此相似.我们形象地称为“母子相似”。（3）类型为旋转型。（如图）以上几种相似三角形的基本类型在识别两个三角形相似时非常有用，并且常常与平移、旋转、对称等图形的运动结合。在复杂图形的背景下识别两三角形相似，也离不开以上几种基本图形，因此，一定要熟练掌握。 如果△ABC∽△A′B′C′的相似比为k，即指k，那么△A′B′C′∽△ABC的相似比就是了。
教学环节 教学内容 设计意图
【例1】如图，点O是△ABC的两条角平分线的交点，过O作AO的垂线交AB于D。求证：△OBD∽△CBO。分析：此题不易得到边的比例关系，但O点是三角形的角平分线的交点，有多对相等的角，故宜从角相等方面去考虑。由角平分线及三角形内角和定理知：∠1＋∠2＋∠DAO＝900，再由AO⊥DO可得∠5＝∠1＋∠2，而∠5＝∠3＋∠4，从而∠1＋∠2＝∠3＋∠4，由∠1＝∠3可得∠2＝∠4，于是结论得证。 变式1：已知如图，在△ABC中，AD＝AE，AO⊥DE于O，DE交AB于D，交AC于E，BO平分∠ABC。求证：。变式2：已知如图（同变式1图），在△ABC中，O为两内角平分线的交点，过点O作直线交AB于D，交AC于E，且AD＝AE。求证：（1）△BDO∽△OEC；（2）。【例2】如图，在△ABC中，∠BAC＝900，AD⊥BC于D，E为AC中点，DE交BA的延长线于F。求证：AB∶AC＝BF∶DF。分析：由于△ABC和△FBD一个是直角三角形，一个是钝角三角形，不可能由这一对三角形相似直接找到对应边而得结论，势必要找“过渡”的线段或线段比，这种寻找“中间”搭桥的线段或线段比是重要的解题技巧。
教学环节 教学内容 设计意图
证明：∵AB⊥AC，AD⊥BC ∴Rt△ABD∽Rt△CAD，∠DAC＝∠B ∴………①又∵AD⊥BC，E为AC中点∴DE＝AE，∠DAE＝∠ADE∴∠B＝∠ADE又∵∠F＝∠F∴△FAD∽△FDB∴………②由①②得变式：本题条件、结论不变，而只改变图形的位置时，如下图所示，本题又该怎样证明呢？
作业设计
板书设计
教学随笔或教学反思
（1）有一对等角，找
(2)有两边成比例，找
(3)利用已知三角形相似的关系：若△1∽△2，
△2∽△3，则△1∽△3.
相似三角形
例
2
图
F
E
D
C
B
A
例
2
变式图
1
F
E
D
C
B
A
例
2
变式图
2
F
E
D
C
B
A