5.3 诱导公式-【新教材】人教A版高中数学必修第一册课时练习(Word含答案)
文档属性
| 名称 | 5.3 诱导公式-【新教材】人教A版高中数学必修第一册课时练习(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 30.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-02 00:00:00 | ||
图片预览

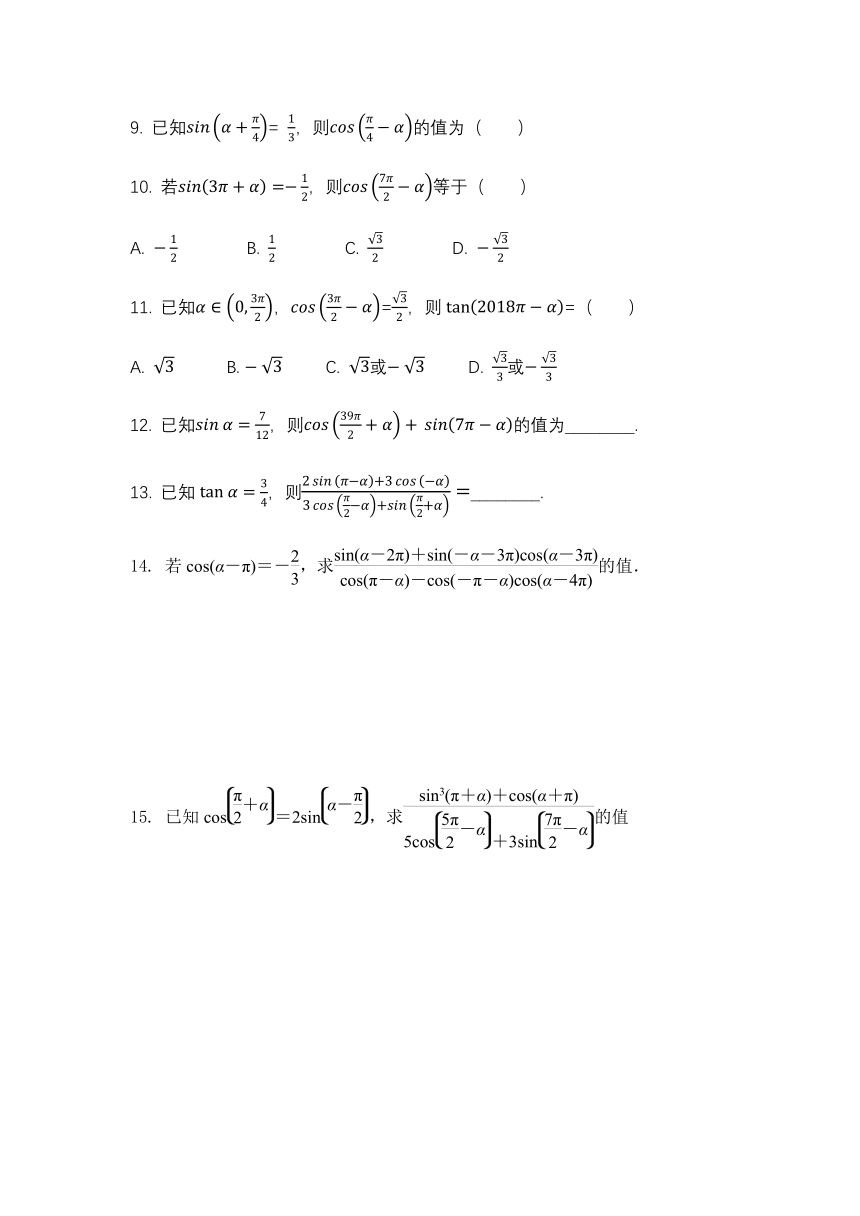

文档简介
5.3 诱导公式
一.给角求值
1. cos5π3的值为( )
A. ?12 B. ?32 C. 12 D. 32
2. cos(?16π3)+sin(?16π3) 的值为( )
A. ?1+32 B. 1?32 C. 3?12 D. 3+12
3. sin6000+tan?(?3000) 的值为( )
A. ?32 B. 32 C. ?12+3 D. 12+3
4. (多选)下列与cos3π2?θ的值相等的是( )
A. sinπ?θ B. sinπ+θ C. cosπ2?θ D. cosπ2+θ
5. sin950+cos1750的值为________.
6. cos?5850sin4950+sin?5700的值等于________.
二.条件求值
7. 已知sinθ=15,则cos450+θ的值是( )
A. 15 B. ?15 C. ?265 D. 265
8. (多选)若cosπ+α=?12,则sinα?2π的值为( )
A. 12 B. ?12 C. 32 D. ?32
9. 已知sinα+π4= 13,则cosπ4?α的值为( )
10. 若sin3π+α=?12,则cos7π2?α等于( )
A. ?12 B. 12 C. 32 D. ?32
11. 已知α∈0,3π2,cos3π2?α=32,则tan2018π?α=( )
A. 3 B. ?3 C. 3或?3 D. 33或?33
12. 已知sin α=712,则cos39π2+α+ sin7π?α的值为________.
13. 已知tan α=34,则2sinπ?α+3cos?α3cosπ2?α+sinπ2+α=________.
14. 若cos(α-π)=-,求的值.
15. 已知cos=2sin,求的值
三.利用诱导公式化简
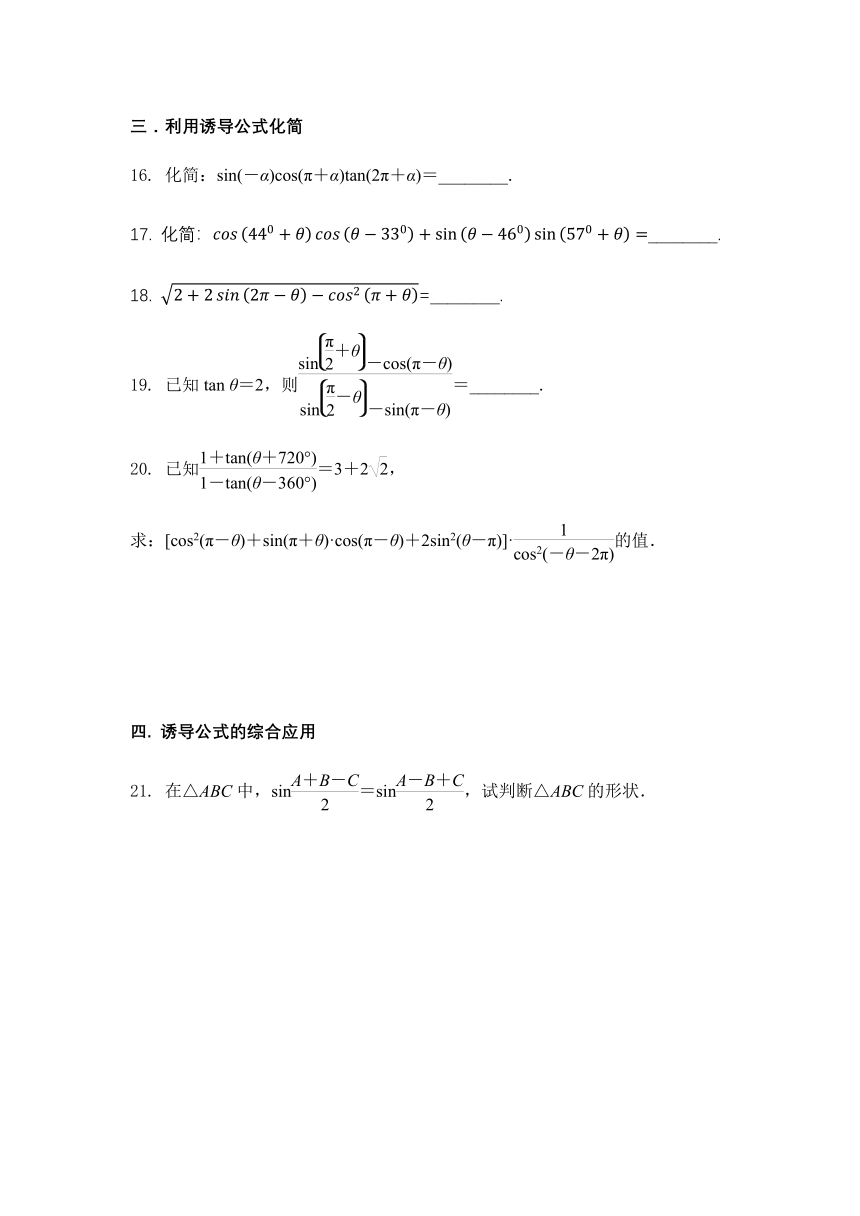
16. 化简:sin(-α)cos(π+α)tan(2π+α)=________.
17. 化简:cos440+θcosθ?330+sinθ?460sin570+θ=________.
18. 2+2sin2π?θ?cos2π+θ=________.
19. 已知tan θ=2,则=________.
20. 已知=3+2,
求:[cos2(π-θ)+sin(π+θ)·cos(π-θ)+2sin2(θ-π)]·的值.
四. 诱导公式的综合应用
21. 在△ABC中,sin=sin,试判断△ABC的形状.
22. 已知f(α)=.
(1)化简f(α);
(2)若α是第三象限的角,且cos=,求f(α)的值;
(3)若α=-,求f(α)的值.
23. 若sin α=,
求+的值.
参考答案
1.C 2.C 3.B 4.BD 5. 0 6.2?2 7.B 8.CD 9.C 10.A 11.B 12.76 13.1813
14. [解] 原式=
==
=-tan α.
∵cos(α-π)=cos(π-α)=-cos α=-,
∴cos α=,∴α为第一象限角或第四象限角.
当α为第一象限角时,cos α=,
sin α==,
∴tan α==,∴原式=-.
当α为第四象限角时,cos α=,
sin α=-=-,
∴tan α==-,∴原式=.
综上,原式=±.
15. [解] ∵cos=2sin,
∴-sin α=-2cos α,∴tan α=2,
∴
=
==
==
===-.
16. sin2α 17. 0 18.1?sinθ 19. -2
20. [解] 由=3+2,
得(4+2)tan θ=2+2,
所以tan θ==,
故[cos2(π-θ)+sin(π+θ)·cos(π-θ)+2sin2(θ-π)]·
=(cos2θ+sin θcos θ+2sin2θ)·
=1+tan θ+2tan2θ=1++2×2=2+.
21. [解] ∵A+B+C=π,
∴A+B-C=π-2C,A-B+C=π-2B.
又∵sin=sin,
∴sin=sin,
∴sin=sin,
∴cos C=cos B.
又B,C为△ABC的内角,∴C=B,
∴△ABC为等腰三角形.
22. [解] (1)f(α)==-cos α.
(2)∵cos=-sin α,
∴sin α=-,
又α是第三象限的角,
∴cos α=-=-,
∴f(α)=.
(3)f=-cos
=-cos
=-cos=-cos =-.
23. [解] +
=+
=+
=+=.
∵sin α=,
∴=10.
一.给角求值
1. cos5π3的值为( )
A. ?12 B. ?32 C. 12 D. 32
2. cos(?16π3)+sin(?16π3) 的值为( )
A. ?1+32 B. 1?32 C. 3?12 D. 3+12
3. sin6000+tan?(?3000) 的值为( )
A. ?32 B. 32 C. ?12+3 D. 12+3
4. (多选)下列与cos3π2?θ的值相等的是( )
A. sinπ?θ B. sinπ+θ C. cosπ2?θ D. cosπ2+θ
5. sin950+cos1750的值为________.
6. cos?5850sin4950+sin?5700的值等于________.
二.条件求值
7. 已知sinθ=15,则cos450+θ的值是( )
A. 15 B. ?15 C. ?265 D. 265
8. (多选)若cosπ+α=?12,则sinα?2π的值为( )
A. 12 B. ?12 C. 32 D. ?32
9. 已知sinα+π4= 13,则cosπ4?α的值为( )
10. 若sin3π+α=?12,则cos7π2?α等于( )
A. ?12 B. 12 C. 32 D. ?32
11. 已知α∈0,3π2,cos3π2?α=32,则tan2018π?α=( )
A. 3 B. ?3 C. 3或?3 D. 33或?33
12. 已知sin α=712,则cos39π2+α+ sin7π?α的值为________.
13. 已知tan α=34,则2sinπ?α+3cos?α3cosπ2?α+sinπ2+α=________.
14. 若cos(α-π)=-,求的值.
15. 已知cos=2sin,求的值
三.利用诱导公式化简
16. 化简:sin(-α)cos(π+α)tan(2π+α)=________.
17. 化简:cos440+θcosθ?330+sinθ?460sin570+θ=________.
18. 2+2sin2π?θ?cos2π+θ=________.
19. 已知tan θ=2,则=________.
20. 已知=3+2,
求:[cos2(π-θ)+sin(π+θ)·cos(π-θ)+2sin2(θ-π)]·的值.
四. 诱导公式的综合应用
21. 在△ABC中,sin=sin,试判断△ABC的形状.
22. 已知f(α)=.
(1)化简f(α);
(2)若α是第三象限的角,且cos=,求f(α)的值;
(3)若α=-,求f(α)的值.
23. 若sin α=,
求+的值.
参考答案
1.C 2.C 3.B 4.BD 5. 0 6.2?2 7.B 8.CD 9.C 10.A 11.B 12.76 13.1813
14. [解] 原式=
==
=-tan α.
∵cos(α-π)=cos(π-α)=-cos α=-,
∴cos α=,∴α为第一象限角或第四象限角.
当α为第一象限角时,cos α=,
sin α==,
∴tan α==,∴原式=-.
当α为第四象限角时,cos α=,
sin α=-=-,
∴tan α==-,∴原式=.
综上,原式=±.
15. [解] ∵cos=2sin,
∴-sin α=-2cos α,∴tan α=2,
∴
=
==
==
===-.
16. sin2α 17. 0 18.1?sinθ 19. -2
20. [解] 由=3+2,
得(4+2)tan θ=2+2,
所以tan θ==,
故[cos2(π-θ)+sin(π+θ)·cos(π-θ)+2sin2(θ-π)]·
=(cos2θ+sin θcos θ+2sin2θ)·
=1+tan θ+2tan2θ=1++2×2=2+.
21. [解] ∵A+B+C=π,
∴A+B-C=π-2C,A-B+C=π-2B.
又∵sin=sin,
∴sin=sin,
∴sin=sin,
∴cos C=cos B.
又B,C为△ABC的内角,∴C=B,
∴△ABC为等腰三角形.
22. [解] (1)f(α)==-cos α.
(2)∵cos=-sin α,
∴sin α=-,
又α是第三象限的角,
∴cos α=-=-,
∴f(α)=.
(3)f=-cos
=-cos
=-cos=-cos =-.
23. [解] +
=+
=+
=+=.
∵sin α=,
∴=10.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
