4.5.3函数模型的应用-【新教材】人教A版(2019)高中数学必修第一册课时练习(Word含答案)
文档属性
| 名称 | 4.5.3函数模型的应用-【新教材】人教A版(2019)高中数学必修第一册课时练习(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 43.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-02 00:00:00 | ||
图片预览


文档简介
4.5.3 函数模型的应用
一. 利用已知函数模型解决实际问题
1.人们通常以分贝(符号是dB)为单位来表示声音强度的等级,强度为x的声音对应的等级为fx=10lgx10?2(dB). 喷气式飞机起飞时,声音约为140dB,一般说话时,声音约为60dB,则喷气式飞机起飞时的声音强度是一般说话时声音强度的( )
A. 73 倍 B. 1073 倍 C. 8 倍 D. 108倍
2. 射线测厚技术原理公式为I=I0??ρμt,其中,I,I0分别为射线穿过被测物前后的强度,e是自然对数的底数,为被测物厚度,ρ为被测物的密度,以是被测物对射线的吸收系数工业上通常用241(Am)低能γ射线测量钢板的原度若这种射线对钢板的半价层厚度为8,钢的密7(多选)某工厂生产一种溶液,按市场要求杂质含量度为7.6,则这种射线的吸收系数为( )
(注:半价层厚度是指将已知射线强度减弱为一半的某种物质厚度,ln2≈0.6931,结果精确到0.001)
0.110 B. 0.112 C. 0.114 D. 0.116
3. 光线通过一块玻璃,强度要损失10%设光线原来的强度为k,通过x块这样的玻璃以后强度为y,则经过x块这样的玻璃后光线强度为y=k·0.9x,那么至少通过________块这样的玻璃,光线强度能减弱到原来的14以下(lg3≈0.477,lg2≈0.3) ( )
A. 12 B. 13 C. 14 D. 15
二. 建立函数模型解决实际问题
4. .20世纪初,辽东半岛大连普兰店东部发现古莲子,其寿命在千年以上,至今大部分还能发芽开花,已知碳14半衰期为5730年(注:半衰期为放射性元素残留量降为原来的一半所需要的时间),若1单位的碳14经过x年后剩余量为y单位,则y关于x的函数表达式是( )
A. y=2?x5730 B. y=2x5730 C. y=1?2?x5730 D. y=1?2?5730x
5. 春天来了,某池塘中的荷花枝繁叶茂,已知每一天新长出荷叶覆盖水面面积是前一天的2倍,若荷叶20天可以完全长满池塘水面,则当荷叶刚好覆盖水面面积一半时,荷叶已生长了( )
A.10天 B.15天 C.19天 D.2天
6. (多选)某工厂生产一种溶液,按市场要求杂质含量不得超过0.1%,而这种溶液最初的杂质含量为2%,现进行过滤,已知每过滤一次杂质含量减少13,则使产品达到市场要求的过滤次数可以为(参考数据: lg2≈0.031,lg3≈0.477)( )
A.6 B.9 C.8 D.7
7. 某企业生产A,B两种型号的产品,每年的产量分别为10万支和40万支,为了扩大再生产,决定对两种产品的生产线进行升级改造,预计改造后的A,B两种产品的年产量的增长率分别为50%和20%,那么至少经过________年后,A产品的年产量会超过B产品的年产量(lg2≈0.031)( )
A. 6年 B. 7年 C. 8年 D. 9年
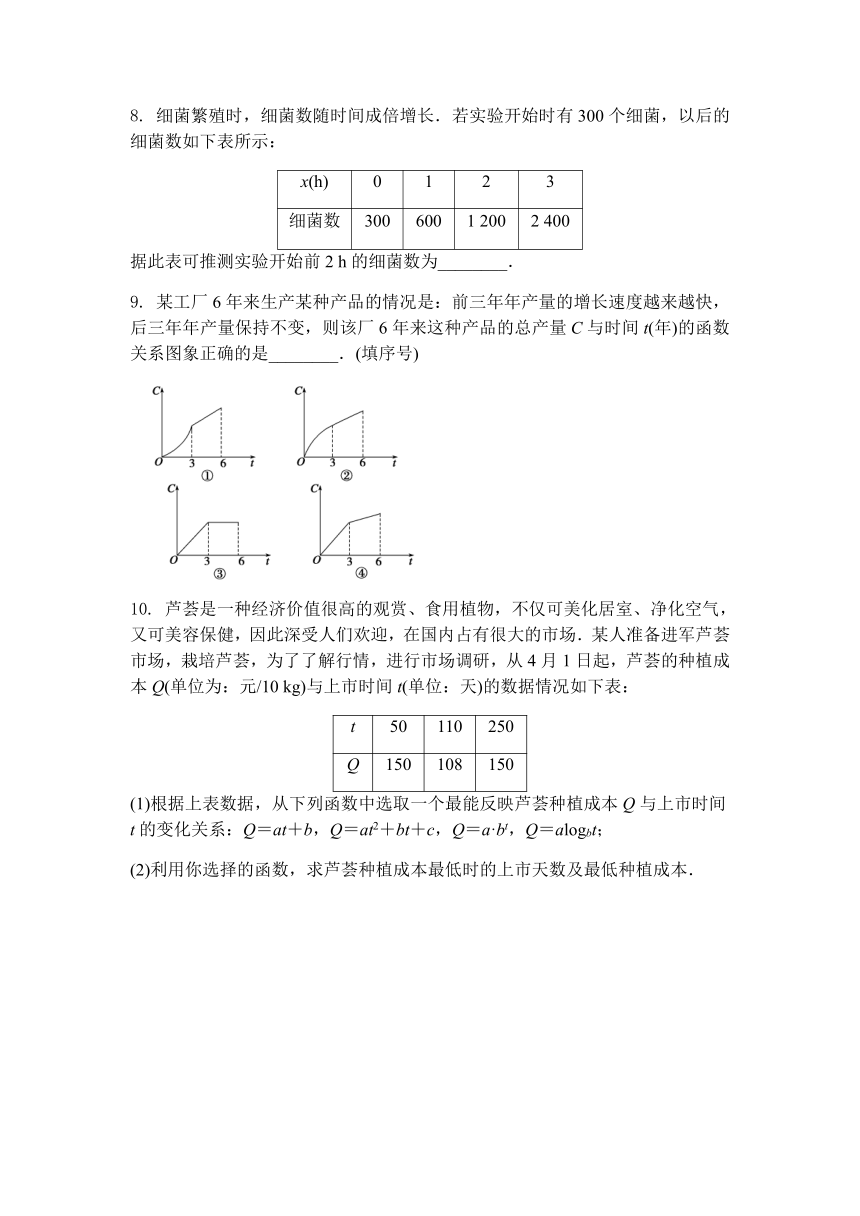
8. 细菌繁殖时,细菌数随时间成倍增长.若实验开始时有300个细菌,以后的细菌数如下表所示:
x(h)
0
1
2
3
细菌数
300
600
1 200
2 400
据此表可推测实验开始前2 h的细菌数为________.
9. 某工厂6年来生产某种产品的情况是:前三年年产量的增长速度越来越快,后三年年产量保持不变,则该厂6年来这种产品的总产量C与时间t(年)的函数关系图象正确的是________.(填序号)
16764015240
10. 芦荟是一种经济价值很高的观赏、食用植物,不仅可美化居室、净化空气,又可美容保健,因此深受人们欢迎,在国内占有很大的市场.某人准备进军芦荟市场,栽培芦荟,为了了解行情,进行市场调研,从4月1日起,芦荟的种植成本Q(单位为:元/10 kg)与上市时间t(单位:天)的数据情况如下表:
t
50
110
250
Q
150
108
150
(1)根据上表数据,从下列函数中选取一个最能反映芦荟种植成本Q与上市时间t的变化关系:Q=at+b,Q=at2+bt+c,Q=a·bt,Q=alogbt;
(2)利用你选择的函数,求芦荟种植成本最低时的上市天数及最低种植成本.
11. 某工厂生产一种电脑元件,每月的生产数据如表:
月份
1
2
3
产量(千件)
50
52
53.9
为估计以后每月对该电脑元件的产量,以这三个月的产量为依据,用函数y=ax+b或y=ax+b(a,b为常数,且a>0)来模拟这种电脑元件的月产量y千件与月份的关系.请问:用以上哪个模拟函数较好?说明理由.
12.一片森林原来的面积为a,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的,已知到今年为止,森林剩余面积为原来的,(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
参考答案
1.D 2.C 3.C 4.A 5.C 6.BC 7.B 8. 75 9. ①
10. 解 (1)由所提供的数据可知,刻画芦荟种植成本Q与上市时间t的变化关系的函数不可能是常值函数,若用函数Q=at+b,Q=a·bt,Q=alogbt中的任意一个来反映时都应有a≠0,且上述三个函数均为单调函数,这与表格所提供的数据不符合,所以应选用二次函数Q=at2+bt+c进行描述.将表格所提供的三组数据分别代入函数Q=at2+bt+c,可得:
解得a=,b=-,c=.
所以,刻画芦荟种植成本Q与上市时间t的变化关系的函数为Q=t2-t+.
(2)当t=-=150(天)时,芦荟种植成本最低为
Q=×1502-×150+=100(元/10 kg).
11. 解 将(1,50)、(2,52)分别代入两解析式得:
或(a>0)
解得(两方程组的解相同).
∴两函数分别为y=2x+48或y=2x+48.
当x=3时,对于y=2x+48有y=54;
当x=3时,对于y=2x+48有y=56.
由于56与53.9的误差较大,
∴选y=ax+b较好.
12. 解 (1)设每年砍伐面积的百分比为x(0a(1-x)10=a,即(1-x)10=,
解得x=1-false.
(2)设经过m年剩余面积为原来的,则
a(1-x)m=a,即false=false,=,解得m=5,
故到今年为止,已砍伐了5年.
(3)设从今年开始,以后砍了n年,
则n年后剩余面积为a(1-x)n.
令a(1-x)n≥a,即(1-x)n≥,
false≥false,≤,解得n≤15.
故今后最多还能砍伐15年.
一. 利用已知函数模型解决实际问题
1.人们通常以分贝(符号是dB)为单位来表示声音强度的等级,强度为x的声音对应的等级为fx=10lgx10?2(dB). 喷气式飞机起飞时,声音约为140dB,一般说话时,声音约为60dB,则喷气式飞机起飞时的声音强度是一般说话时声音强度的( )
A. 73 倍 B. 1073 倍 C. 8 倍 D. 108倍
2. 射线测厚技术原理公式为I=I0??ρμt,其中,I,I0分别为射线穿过被测物前后的强度,e是自然对数的底数,为被测物厚度,ρ为被测物的密度,以是被测物对射线的吸收系数工业上通常用241(Am)低能γ射线测量钢板的原度若这种射线对钢板的半价层厚度为8,钢的密7(多选)某工厂生产一种溶液,按市场要求杂质含量度为7.6,则这种射线的吸收系数为( )
(注:半价层厚度是指将已知射线强度减弱为一半的某种物质厚度,ln2≈0.6931,结果精确到0.001)
0.110 B. 0.112 C. 0.114 D. 0.116
3. 光线通过一块玻璃,强度要损失10%设光线原来的强度为k,通过x块这样的玻璃以后强度为y,则经过x块这样的玻璃后光线强度为y=k·0.9x,那么至少通过________块这样的玻璃,光线强度能减弱到原来的14以下(lg3≈0.477,lg2≈0.3) ( )
A. 12 B. 13 C. 14 D. 15
二. 建立函数模型解决实际问题
4. .20世纪初,辽东半岛大连普兰店东部发现古莲子,其寿命在千年以上,至今大部分还能发芽开花,已知碳14半衰期为5730年(注:半衰期为放射性元素残留量降为原来的一半所需要的时间),若1单位的碳14经过x年后剩余量为y单位,则y关于x的函数表达式是( )
A. y=2?x5730 B. y=2x5730 C. y=1?2?x5730 D. y=1?2?5730x
5. 春天来了,某池塘中的荷花枝繁叶茂,已知每一天新长出荷叶覆盖水面面积是前一天的2倍,若荷叶20天可以完全长满池塘水面,则当荷叶刚好覆盖水面面积一半时,荷叶已生长了( )
A.10天 B.15天 C.19天 D.2天
6. (多选)某工厂生产一种溶液,按市场要求杂质含量不得超过0.1%,而这种溶液最初的杂质含量为2%,现进行过滤,已知每过滤一次杂质含量减少13,则使产品达到市场要求的过滤次数可以为(参考数据: lg2≈0.031,lg3≈0.477)( )
A.6 B.9 C.8 D.7
7. 某企业生产A,B两种型号的产品,每年的产量分别为10万支和40万支,为了扩大再生产,决定对两种产品的生产线进行升级改造,预计改造后的A,B两种产品的年产量的增长率分别为50%和20%,那么至少经过________年后,A产品的年产量会超过B产品的年产量(lg2≈0.031)( )
A. 6年 B. 7年 C. 8年 D. 9年
8. 细菌繁殖时,细菌数随时间成倍增长.若实验开始时有300个细菌,以后的细菌数如下表所示:
x(h)
0
1
2
3
细菌数
300
600
1 200
2 400
据此表可推测实验开始前2 h的细菌数为________.
9. 某工厂6年来生产某种产品的情况是:前三年年产量的增长速度越来越快,后三年年产量保持不变,则该厂6年来这种产品的总产量C与时间t(年)的函数关系图象正确的是________.(填序号)
16764015240
10. 芦荟是一种经济价值很高的观赏、食用植物,不仅可美化居室、净化空气,又可美容保健,因此深受人们欢迎,在国内占有很大的市场.某人准备进军芦荟市场,栽培芦荟,为了了解行情,进行市场调研,从4月1日起,芦荟的种植成本Q(单位为:元/10 kg)与上市时间t(单位:天)的数据情况如下表:
t
50
110
250
Q
150
108
150
(1)根据上表数据,从下列函数中选取一个最能反映芦荟种植成本Q与上市时间t的变化关系:Q=at+b,Q=at2+bt+c,Q=a·bt,Q=alogbt;
(2)利用你选择的函数,求芦荟种植成本最低时的上市天数及最低种植成本.
11. 某工厂生产一种电脑元件,每月的生产数据如表:
月份
1
2
3
产量(千件)
50
52
53.9
为估计以后每月对该电脑元件的产量,以这三个月的产量为依据,用函数y=ax+b或y=ax+b(a,b为常数,且a>0)来模拟这种电脑元件的月产量y千件与月份的关系.请问:用以上哪个模拟函数较好?说明理由.
12.一片森林原来的面积为a,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的,已知到今年为止,森林剩余面积为原来的,(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
参考答案
1.D 2.C 3.C 4.A 5.C 6.BC 7.B 8. 75 9. ①
10. 解 (1)由所提供的数据可知,刻画芦荟种植成本Q与上市时间t的变化关系的函数不可能是常值函数,若用函数Q=at+b,Q=a·bt,Q=alogbt中的任意一个来反映时都应有a≠0,且上述三个函数均为单调函数,这与表格所提供的数据不符合,所以应选用二次函数Q=at2+bt+c进行描述.将表格所提供的三组数据分别代入函数Q=at2+bt+c,可得:
解得a=,b=-,c=.
所以,刻画芦荟种植成本Q与上市时间t的变化关系的函数为Q=t2-t+.
(2)当t=-=150(天)时,芦荟种植成本最低为
Q=×1502-×150+=100(元/10 kg).
11. 解 将(1,50)、(2,52)分别代入两解析式得:
或(a>0)
解得(两方程组的解相同).
∴两函数分别为y=2x+48或y=2x+48.
当x=3时,对于y=2x+48有y=54;
当x=3时,对于y=2x+48有y=56.
由于56与53.9的误差较大,
∴选y=ax+b较好.
12. 解 (1)设每年砍伐面积的百分比为x(0
解得x=1-false.
(2)设经过m年剩余面积为原来的,则
a(1-x)m=a,即false=false,=,解得m=5,
故到今年为止,已砍伐了5年.
(3)设从今年开始,以后砍了n年,
则n年后剩余面积为a(1-x)n.
令a(1-x)n≥a,即(1-x)n≥,
false≥false,≤,解得n≤15.
故今后最多还能砍伐15年.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
