实数中考复习
图片预览

文档简介
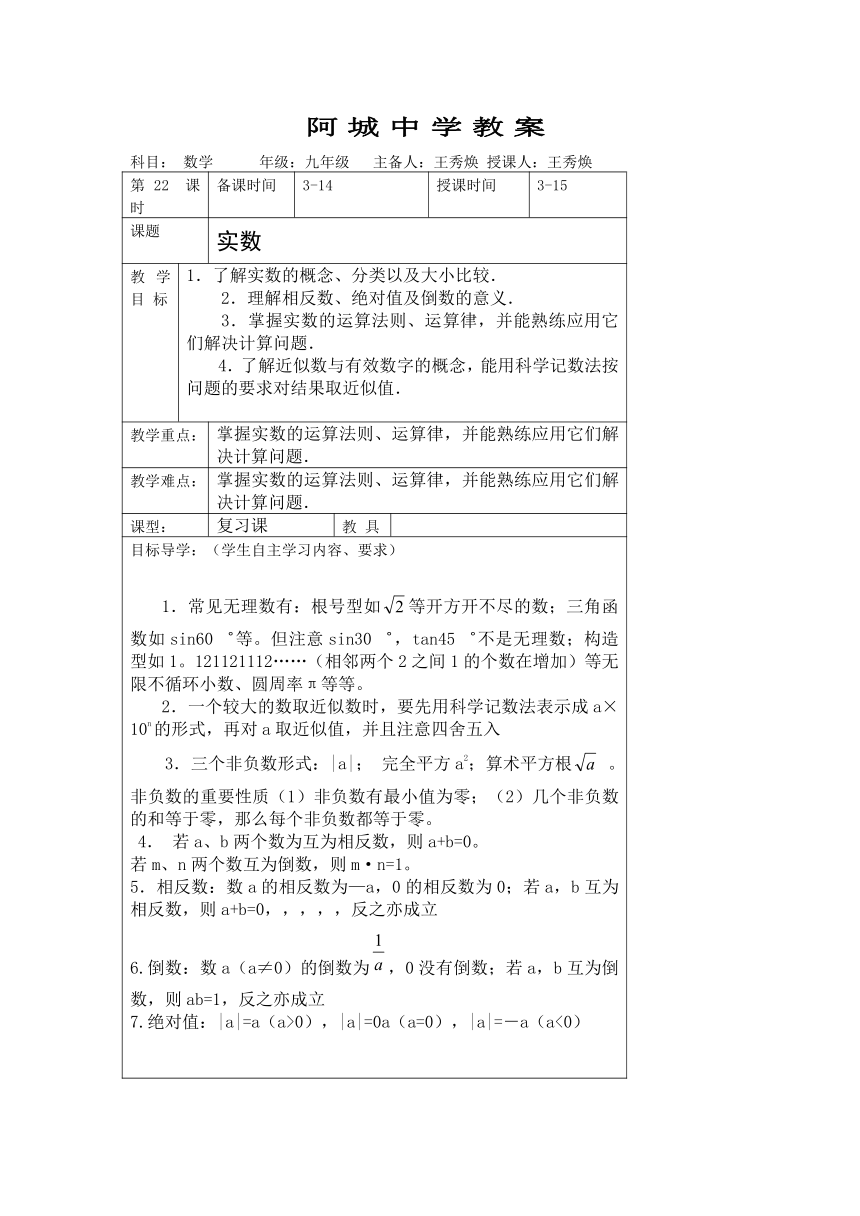
阿城中学教案
科目: 数学 年级:九年级 主备人:王秀焕 授课人:王秀焕
第 22 课时 备课时间 3-14 授课时间 3-15
课题 实数
教学目 标 1.了解实数的概念、分类以及大小比较. 2.理解相反数、绝对值及倒数的意义. 3.掌握实数的运算法则、运算律,并能熟练应用它们解决计算问题.4.了解近似数与有效数字的概念,能用科学记数法按问题的要求对结果取近似值.
教学重点: 掌握实数的运算法则、运算律,并能熟练应用它们解决计算问题.
教学难点: 掌握实数的运算法则、运算律,并能熟练应用它们解决计算问题.
课型: 复习课 教 具
目标导学:(学生自主学习内容、要求)1.常见无理数有:根号型如等开方开不尽的数;三角函数如sin60゜等。但注意sin30゜,tan45゜不是无理数;构造型如1。121121112……(相邻两个2之间1的个数在增加)等无限不循环小数、圆周率π等等。2.一个较大的数取近似数时,要先用科学记数法表示成a×10n的形式,再对a取近似值,并且注意四舍五入3.三个非负数形式:|a|; 完全平方a2;算术平方根 。非负数的重要性质(1)非负数有最小值为零;(2)几个非负数的和等于零,那么每个非负数都等于零。 4. 若a、b两个数为互为相反数,则a+b=0。若m、n两个数互为倒数,则m·n=1。5.相反数:数a的相反数为—a,0的相反数为0;若a,b互为相反数,则a+b=0,,,,,反之亦成立6.倒数:数a(a≠0)的倒数为,0没有倒数;若a,b互为倒数,则ab=1,反之亦成立7.绝对值:|a|=a(a>0),|a|=0a(a=0),|a|=-a(a<0)
学生自主学习小组讨论(提问问题、导学探究讨论内容、方式等)【例题1】 (河南)2005年末我国外汇储备达到8 189亿美元,8 189亿用科学记数法表示(保留3个有效数字)是( ). A.8.19×1011 B.8.18×1011 C.8.19×1012 D.8.18×1012 评析:正确理解近似数的精确度及有效数字等概念,精确到哪一位,保留几个有效数字,因此,8 189亿=818 900 000 000,用科学记数法表示为8.19×1011,保留3个有效数字为8.19×1011,故选A. 【例题2】 若a的倒数是-1,b+2与a-3互为相反数,c的绝对值为2,且ac>0,试比较:b+c与ab的大小. 评析:根据倒数、相反数、绝对值的意义,可首先求出a、b、c的值,再对b+c与ab进行大小比较. 答案:b+c>ab【例题3】 计算: (1)103+()-2×(-7)0-(-3)3×0.3-1+│-5│+5;(2)(5.7)÷(-)-4.3×13+(-+)×30. 解:(1)原式=1 000+900×1-(-27)×+5+5=1 000+900+90+5+5=2 000. (2)原式=-5.7×13-4.3×13-12+25=-5.7×13-4.3×13+13=13(-5.7-4.3+1)=-117. 评析:(1)题中含有加、减、乘、除、乘方运算,计算此类型题目,应注意运算顺序:先算乘方,再算乘除,最后算加减.(2)恰当运用乘法分配律,可使运算简便.
交流展示(内容、方式、过程等)实数的运算 (1)加法 同号两数相加,取原来的符号,并把绝对值相加; 异号两数相加。取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值; 任何数与零相加等于原数。 (2)减法 a-b=a+(-b) (3)乘法 两数相乘,同号得正,异号得负,并把绝对值相乘;零乘以任何数都得零.即 (4)除法 (5)乘方 (6)开方 如果x2=a且x≥0,那么=x; 如果x3=a,那么在同一个式于里,先乘方、开方,然后乘、除,最后加、减.有括号时,先算括号里面.3.实数的运算律 (1)加法交换律 a+b=b+a (2)加法结合律 (a+b)+c=a+(b+c) (3)乘法交换律 ab=ba. (4)乘法结合律 (ab)c=a(bc)
归纳总结(教师总结、释难解疑及师生互动探究)在理解实数的有关概念、法则的基础上,仔细认真地对题目进行观察、理解,根据题目的具体条件,将推理与计算相结合、灵活巧妙地选择合理简捷的算法解决问题,从而提高运算能力,发展思维的敏捷性与灵活性
练习反馈:1.我国1990年的人口出生数为23784659人。保留三个有效数字的近似值是 人。2.由四舍五入法得到的近似数3.10×104,它精确到 位。这个近似值的有效数字是 。3.2的相反数与倒数的和的绝对值等于 。4.已知:|x|=4,y2=且x>0,y<0,则x-y= 5.计算(1)-32-[(-2)3÷(-)-2+2×(-2.11)0]÷(-5)×.(2)[×(-2)2-()2]÷| 22011·(-)2012| .(3)0.3-1-(- )-2+43-3-1+(π-3)0+tan230°
板书设计: 实数相关概念 计算法则 典型例题
课后反思:进入第一轮复习,对同学们来说打好基础是关键。力争通过复习,能使学生形成知识网络。
科目: 数学 年级:九年级 主备人:王秀焕 授课人:王秀焕
第 22 课时 备课时间 3-14 授课时间 3-15
课题 实数
教学目 标 1.了解实数的概念、分类以及大小比较. 2.理解相反数、绝对值及倒数的意义. 3.掌握实数的运算法则、运算律,并能熟练应用它们解决计算问题.4.了解近似数与有效数字的概念,能用科学记数法按问题的要求对结果取近似值.
教学重点: 掌握实数的运算法则、运算律,并能熟练应用它们解决计算问题.
教学难点: 掌握实数的运算法则、运算律,并能熟练应用它们解决计算问题.
课型: 复习课 教 具
目标导学:(学生自主学习内容、要求)1.常见无理数有:根号型如等开方开不尽的数;三角函数如sin60゜等。但注意sin30゜,tan45゜不是无理数;构造型如1。121121112……(相邻两个2之间1的个数在增加)等无限不循环小数、圆周率π等等。2.一个较大的数取近似数时,要先用科学记数法表示成a×10n的形式,再对a取近似值,并且注意四舍五入3.三个非负数形式:|a|; 完全平方a2;算术平方根 。非负数的重要性质(1)非负数有最小值为零;(2)几个非负数的和等于零,那么每个非负数都等于零。 4. 若a、b两个数为互为相反数,则a+b=0。若m、n两个数互为倒数,则m·n=1。5.相反数:数a的相反数为—a,0的相反数为0;若a,b互为相反数,则a+b=0,,,,,反之亦成立6.倒数:数a(a≠0)的倒数为,0没有倒数;若a,b互为倒数,则ab=1,反之亦成立7.绝对值:|a|=a(a>0),|a|=0a(a=0),|a|=-a(a<0)
学生自主学习小组讨论(提问问题、导学探究讨论内容、方式等)【例题1】 (河南)2005年末我国外汇储备达到8 189亿美元,8 189亿用科学记数法表示(保留3个有效数字)是( ). A.8.19×1011 B.8.18×1011 C.8.19×1012 D.8.18×1012 评析:正确理解近似数的精确度及有效数字等概念,精确到哪一位,保留几个有效数字,因此,8 189亿=818 900 000 000,用科学记数法表示为8.19×1011,保留3个有效数字为8.19×1011,故选A. 【例题2】 若a的倒数是-1,b+2与a-3互为相反数,c的绝对值为2,且ac>0,试比较:b+c与ab的大小. 评析:根据倒数、相反数、绝对值的意义,可首先求出a、b、c的值,再对b+c与ab进行大小比较. 答案:b+c>ab【例题3】 计算: (1)103+()-2×(-7)0-(-3)3×0.3-1+│-5│+5;(2)(5.7)÷(-)-4.3×13+(-+)×30. 解:(1)原式=1 000+900×1-(-27)×+5+5=1 000+900+90+5+5=2 000. (2)原式=-5.7×13-4.3×13-12+25=-5.7×13-4.3×13+13=13(-5.7-4.3+1)=-117. 评析:(1)题中含有加、减、乘、除、乘方运算,计算此类型题目,应注意运算顺序:先算乘方,再算乘除,最后算加减.(2)恰当运用乘法分配律,可使运算简便.
交流展示(内容、方式、过程等)实数的运算 (1)加法 同号两数相加,取原来的符号,并把绝对值相加; 异号两数相加。取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值; 任何数与零相加等于原数。 (2)减法 a-b=a+(-b) (3)乘法 两数相乘,同号得正,异号得负,并把绝对值相乘;零乘以任何数都得零.即 (4)除法 (5)乘方 (6)开方 如果x2=a且x≥0,那么=x; 如果x3=a,那么在同一个式于里,先乘方、开方,然后乘、除,最后加、减.有括号时,先算括号里面.3.实数的运算律 (1)加法交换律 a+b=b+a (2)加法结合律 (a+b)+c=a+(b+c) (3)乘法交换律 ab=ba. (4)乘法结合律 (ab)c=a(bc)
归纳总结(教师总结、释难解疑及师生互动探究)在理解实数的有关概念、法则的基础上,仔细认真地对题目进行观察、理解,根据题目的具体条件,将推理与计算相结合、灵活巧妙地选择合理简捷的算法解决问题,从而提高运算能力,发展思维的敏捷性与灵活性
练习反馈:1.我国1990年的人口出生数为23784659人。保留三个有效数字的近似值是 人。2.由四舍五入法得到的近似数3.10×104,它精确到 位。这个近似值的有效数字是 。3.2的相反数与倒数的和的绝对值等于 。4.已知:|x|=4,y2=且x>0,y<0,则x-y= 5.计算(1)-32-[(-2)3÷(-)-2+2×(-2.11)0]÷(-5)×.(2)[×(-2)2-()2]÷| 22011·(-)2012| .(3)0.3-1-(- )-2+43-3-1+(π-3)0+tan230°
板书设计: 实数相关概念 计算法则 典型例题
课后反思:进入第一轮复习,对同学们来说打好基础是关键。力争通过复习,能使学生形成知识网络。
同课章节目录
