2.1平方差公式学案 青岛版

课题：2、1 平方差公式
一、教与学目标：
1、会推导平方差公式(a+b)(a-b)=a2-b2了解公式的几何解释，理解公式数学表达式与文字表达式在应用上的差异。并能运用公式进行计算。
2、经历探索平方差公式的推导过程，体会“特殊——一般——特殊”的认识规律。
二、教与学重点和难点：
公式的应用及推广
三、教与学方法：自主探究，合作交流
四、教学过程
（一）情境引入：
时代中学计划将一个边长为m米的正方形花坛改造成长为（m+1）米、宽为（m-1）米的长方形的花坛。你会计算改造后的花坛面积吗？
（m+1）×（m-1）=m2+m-m-1=m2-1
你能说出上面乘式中两个因式以及它们的特征吗？
由多项式的乘法法则可以得到
（a+b）（a-b）=a2+ab-ab+b2=a2-b2
从而有下面的平方差公式（a+b）（a-b）=a2-b2
（二）自主学习 探究新知
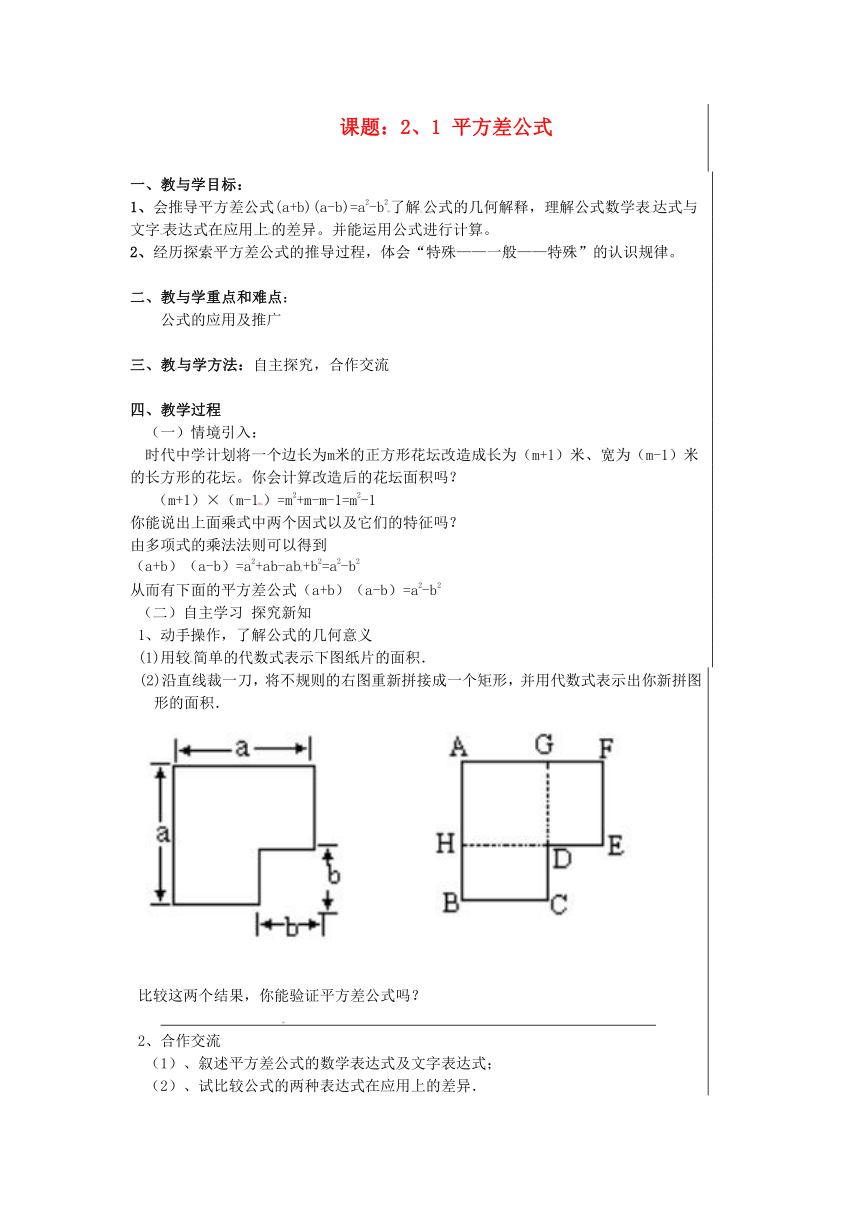
1、动手操作，了解公式的几何意义
(1)用较简单的代数式表示下图纸片的面积．
(2)沿直线裁一刀，将不规则的右图重新拼接成一个矩形，并用代数式表示出你新拼图形的面积．
比较这两个结果，你能验证平方差公式吗？
2、合作交流
（1）、叙述平方差公式的数学表达式及文字表达式；
（2）、试比较公式的两种表达式在应用上的差异．
依照公式的文字表达式可写出下面两个正确的式子：
（3）．判断正误：
(4x+3b)(4x-3b)＝4x2-3b2；( ) (4x+3b)(4x-3b)＝16x2-9； ( )
(4x+3b)(4x-3b)＝4x2+9b2 ( ) (4x+3b)(4x-3b)＝4x2-9b2； ( )
（4）例1 利用平方差公式计算：
(3x+2y)3(x-2y) (-7+2m2)(-7-2m2)
温新提示：平方差公式中的a、b可以表示任意的代数式
（三）、学以致用
1、 运用平方差公式计算：
(1)102×98； (2)(y+2)(y-2)(y2+4)．
2．运用平方差公式计算：
(1)103×97； (2)(x+3)(x-3)(x2+9)；
(3)59.8×60.2；
3、 填空：
1）、(1)a2-4＝(a+2)( )；(2) 25-x2＝ (5-x) ( )；(3)m2-n2＝( )( )；
2）、x2-25＝( )( )；
3）、4m2-49＝(2m-7)( )；
4）、a4-m4＝(a2+m2)( )＝(a2+m2)( )( )；
4、计算：
(1)(a+b-3)(a+b+3)； (2)(m2+n-7)(m2-n-7)．
（四）拓展延伸 迁移升华
1．运用平方差公式计算：
(1)(a2+b)(a2-b)； (2)(-4m2+5n)(4m2+5n)；
(3)(x2-y2)(x2+y2)；(4)(9a2+7b2)(7b2-9a2)．
2．运用平方差公式计算：
五课堂小结：
1．什么是平方差公式？一般两个二项式相乘的积应是几项式？
2．平方差公式中字母a、b可以是那些形式？
3．怎样判断一个多项式的乘法问题是否可以用平方差公式？
六、作业
1、必做题
习题2.1 A组1 2
B组1 2
2、挑战自我
七、教学反思；