福建省厦门六中2011-2012学年高二下学期期中数学文试卷
文档属性
| 名称 | 福建省厦门六中2011-2012学年高二下学期期中数学文试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 218.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-18 20:35:35 | ||
图片预览



文档简介
厦门六中2011-2012学年下学期高二期中考试
数 学 试 卷(文科)
满分150分 考试时间120分钟 命题人: 2012.04.10
参考公式
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的 )
1.若复数(,为虚数单位)是纯虚数,则实数等于( )
A. B. C.1 D.-1
2.已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( )
A、-12 D、a<-3或a>6
3. 用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是( )
A.假设三内角都不大于60度 B. 假设三内角都大于60度
C. 假设三内角至多有一个大于60度 D. 假设三内角至多有两个大于60度
4. 《论语》云:“名不正,则言不顺;言不顺,则事不成;事不成,则礼乐不兴;礼乐不兴,则刑罚不中;刑罚不中,则民无所措手足;所以名不正,则民无所措手足.”上述推理用的是( )
A.合情推理 B.归纳推理 C.类比推理 D.演绎推理
5. 以下四图都是同一坐标系中三次函数及其导函数的图象,其中一定不正确的序号是( )
A. ③④ B. ①② C. ②③ D. ②④
6. 设<b,函数的图像可能是( )
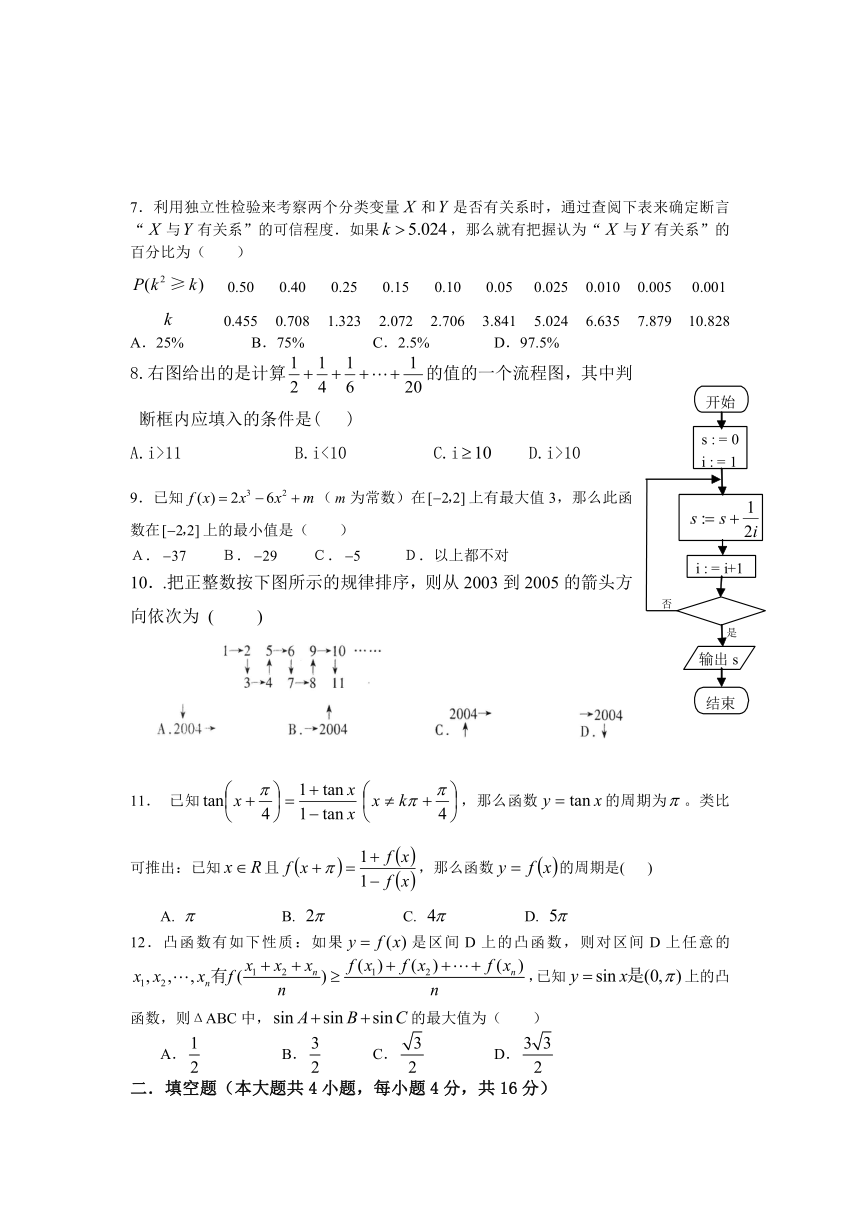
7.利用独立性检验来考察两个分类变量和是否有关系时,通过查阅下表来确定断言“与有关系”的可信程度.如果,那么就有把握认为“与有关系”的百分比为( )
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
A.25% B.75% C.2.5% D.97.5%
8.右图给出的是计算的值的一个流程图,其中判断框内应填入的条件是( )
A.i>11 B.i<10 C.i D.i>10
9.已知(为常数)在上有最大值3,那么此函数在上的最小值是( )
A. B. C. D.以上都不对
10..把正整数按下图所示的规律排序,则从2003到2005的箭头方向依次为 ( )
11. 已知,那么函数的周期为。类比可推出:已知且,那么函数的周期是( )
A. B. C. D.
12.凸函数有如下性质:如果是区间D上的凸函数,则对区间D上任意的,已知上的凸函数,则ΔABC中,的最大值为( )
A. B. C. D.
二.填空题(本大题共4小题,每小题4分,共16分)
13. 与的大小关系是__________.
14.求曲线在点处的切线方程是_______。
15.设复数满足条件那么的最大值是________________.
16.右图是函数的导函数的图象,
给出下列命题:
①是函数的极值点;
②是函数的最小值点;
③在处切线的斜率小于零;
④在区间上单调递增.
则正确命题的序号是
三、解答题:(本大题共6个小题,满分74分,解答时要求写出必要的文字说明或推演步骤。)
17.(本小题12分)设复数满足,且是纯虚数,求。
18.(本小题满分10分)一家新技术公司计划研制一个名片管理系统,`希望系统能够具备以下功能,
1. 用户管理:能修改密码,显示用户信息,修改用户信息。
2.用户登录。
3.名片管理:能够对名片进行删除、添加、修改、查询。
4.出错信息处理。根据这些要求画出该系统的结构图。
19.(本小题满分12分)
某兴趣小组为了研究昼夜温差大小与患感冒人数多少之间的关系,分别到气象站和医院抄录了1至6月份每月15日的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日 期 1月15日 2月15日 3月15日 4月15日 5月15日 6月15日
昼夜温差x(°C) 10 11 13 12 8 6
就诊人数y(个) 22 25 29 26 16 12
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出关于的线性回归方程;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性的回归方程是否理想?
20. (本小题满分12分)已知的三边长为 a、b、c,且其中任意两边长均不相等。若成等差数列。
(1)比较与的大小,并证明你的结论;
(2)求证B不可能是钝角
21.(本小题14分)已知函数在上是增函数,在上是减函数.
(1)求b的值;
(2)当时,曲线总在直线上方,求的取值范围.
22.(本小题14分)已知函数.
(1)若,求曲线在处切线的斜率;
(2)求的单调区间;
(3)设,若对任意,均存在,使得,求的取值范围。
厦门六中2011-2012学年第二学期高二数学期中考试卷
(文科)参考答案
一、CDBD,ACDD,ABCD。二、<,,4,(1)(4)
三、解答题(本大题共6小题,共74分。解答应写出必要的文字说明、证明过程及演算步骤)
17.(本小题12分)
解:设,由得;………………………………(3分)
是纯虚数,则(6分)
, ……………(12分)
18.解:(本小题10分)
19. (本小题12分)解:(1)……………4分
………………………………………………8分
(2) …………………………………………10分
21世纪教育网 …………………………………………………11分
所以所得线性回归方程是理想的。 ………………………………………………12分
20.解:(本小题12分)(1)大小关系为…………………………………(2分)
证明如下:要证,只需证
a、b、c,只需证,成等差数列,
∴∴
又a、b、c,任意两边长均不相等,∴成立
故所得大小关系正确………………………………………(6分)
3
(2)假设B是钝角,则cosB<0,
而这与cosB<0,矛盾,故假设不成立。
∴B不可能是钝角………………………………………(12分)
21.(本小题14分)
解:解:(Ⅰ)∵,
∴. ……………………2分
∵在上是增函数,在上是减函数,
∴ 当时,有极大值,即, ……………………4分
∴ . ……………………6分
(Ⅱ),
∵ 在上是增函数,在上是减函数,
∴,即. ……………………8分
∵曲线在直线的上方,
设, ……………………9分
∴在时,恒成立,∵ ,
令,两个根为,,且, ……………………10分
- +
极小值
∴ 当时,有最小值. ……………………12分
令, ∴,由,
∴ . ……………………14分
另解:,
当a=0时,,,函数在定义域上为增函数,与已知矛盾,舍;……………………7分
当a>0时,由(Ⅰ)知,,
函数在上为增函数,在上为减函数,与已知矛盾,舍;……………………8分
当a<0时,,由已知可得,∴ ……………9分
设, ………………10分
∴ 。
令,两个根为,,,
- +
极小值
∴ 当时,有最小值. ……………………12分
令, ∴,由,
∴ . ……………………14分
22.(本小题14分)
解:(Ⅰ)由已知,………………………………………(2分)
.故曲线在处切线的斜率为.……………(4分)
(Ⅱ).……………………………………………………(5分)
①当时,由于,故,
所以,的单调递增区间为.………………………………………(6分)
②当时,由,得.在区间上,,在区间上,
所以,函数的单调递增区间为,单调递减区间为.…(8分)
(Ⅲ)由已知,转化为.…………………………………………(9分)
……………………………………………………………………(10分)
由(Ⅱ)知,当时,在上单调递增,值域为,故不符合题意.
(或者举出反例:存在,故不符合题意.)……………(11分)
当时,在上单调递增,在上单调递减,
故的极大值即为最大值,,……(13分)
所以解得. ………………………………(14分)
……………………10分
……………………5分
……………………3分
……………………8分
名片管理系统
用户管理
用户登录
名片管理
出错信息处理
能修改密码
显示用户信息
修改用户信息
名片删除
名片添加
名片修改
名片查询
数 学 试 卷(文科)
满分150分 考试时间120分钟 命题人: 2012.04.10
参考公式
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的 )
1.若复数(,为虚数单位)是纯虚数,则实数等于( )
A. B. C.1 D.-1
2.已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( )
A、-1
3. 用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是( )
A.假设三内角都不大于60度 B. 假设三内角都大于60度
C. 假设三内角至多有一个大于60度 D. 假设三内角至多有两个大于60度
4. 《论语》云:“名不正,则言不顺;言不顺,则事不成;事不成,则礼乐不兴;礼乐不兴,则刑罚不中;刑罚不中,则民无所措手足;所以名不正,则民无所措手足.”上述推理用的是( )
A.合情推理 B.归纳推理 C.类比推理 D.演绎推理
5. 以下四图都是同一坐标系中三次函数及其导函数的图象,其中一定不正确的序号是( )
A. ③④ B. ①② C. ②③ D. ②④
6. 设<b,函数的图像可能是( )
7.利用独立性检验来考察两个分类变量和是否有关系时,通过查阅下表来确定断言“与有关系”的可信程度.如果,那么就有把握认为“与有关系”的百分比为( )
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
A.25% B.75% C.2.5% D.97.5%
8.右图给出的是计算的值的一个流程图,其中判断框内应填入的条件是( )
A.i>11 B.i<10 C.i D.i>10
9.已知(为常数)在上有最大值3,那么此函数在上的最小值是( )
A. B. C. D.以上都不对
10..把正整数按下图所示的规律排序,则从2003到2005的箭头方向依次为 ( )
11. 已知,那么函数的周期为。类比可推出:已知且,那么函数的周期是( )
A. B. C. D.
12.凸函数有如下性质:如果是区间D上的凸函数,则对区间D上任意的,已知上的凸函数,则ΔABC中,的最大值为( )
A. B. C. D.
二.填空题(本大题共4小题,每小题4分,共16分)
13. 与的大小关系是__________.
14.求曲线在点处的切线方程是_______。
15.设复数满足条件那么的最大值是________________.
16.右图是函数的导函数的图象,
给出下列命题:
①是函数的极值点;
②是函数的最小值点;
③在处切线的斜率小于零;
④在区间上单调递增.
则正确命题的序号是
三、解答题:(本大题共6个小题,满分74分,解答时要求写出必要的文字说明或推演步骤。)
17.(本小题12分)设复数满足,且是纯虚数,求。
18.(本小题满分10分)一家新技术公司计划研制一个名片管理系统,`希望系统能够具备以下功能,
1. 用户管理:能修改密码,显示用户信息,修改用户信息。
2.用户登录。
3.名片管理:能够对名片进行删除、添加、修改、查询。
4.出错信息处理。根据这些要求画出该系统的结构图。
19.(本小题满分12分)
某兴趣小组为了研究昼夜温差大小与患感冒人数多少之间的关系,分别到气象站和医院抄录了1至6月份每月15日的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日 期 1月15日 2月15日 3月15日 4月15日 5月15日 6月15日
昼夜温差x(°C) 10 11 13 12 8 6
就诊人数y(个) 22 25 29 26 16 12
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出关于的线性回归方程;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性的回归方程是否理想?
20. (本小题满分12分)已知的三边长为 a、b、c,且其中任意两边长均不相等。若成等差数列。
(1)比较与的大小,并证明你的结论;
(2)求证B不可能是钝角
21.(本小题14分)已知函数在上是增函数,在上是减函数.
(1)求b的值;
(2)当时,曲线总在直线上方,求的取值范围.
22.(本小题14分)已知函数.
(1)若,求曲线在处切线的斜率;
(2)求的单调区间;
(3)设,若对任意,均存在,使得,求的取值范围。
厦门六中2011-2012学年第二学期高二数学期中考试卷
(文科)参考答案
一、CDBD,ACDD,ABCD。二、<,,4,(1)(4)
三、解答题(本大题共6小题,共74分。解答应写出必要的文字说明、证明过程及演算步骤)
17.(本小题12分)
解:设,由得;………………………………(3分)
是纯虚数,则(6分)
, ……………(12分)
18.解:(本小题10分)
19. (本小题12分)解:(1)……………4分
………………………………………………8分
(2) …………………………………………10分
21世纪教育网 …………………………………………………11分
所以所得线性回归方程是理想的。 ………………………………………………12分
20.解:(本小题12分)(1)大小关系为…………………………………(2分)
证明如下:要证,只需证
a、b、c,只需证,成等差数列,
∴∴
又a、b、c,任意两边长均不相等,∴成立
故所得大小关系正确………………………………………(6分)
3
(2)假设B是钝角,则cosB<0,
而这与cosB<0,矛盾,故假设不成立。
∴B不可能是钝角………………………………………(12分)
21.(本小题14分)
解:解:(Ⅰ)∵,
∴. ……………………2分
∵在上是增函数,在上是减函数,
∴ 当时,有极大值,即, ……………………4分
∴ . ……………………6分
(Ⅱ),
∵ 在上是增函数,在上是减函数,
∴,即. ……………………8分
∵曲线在直线的上方,
设, ……………………9分
∴在时,恒成立,∵ ,
令,两个根为,,且, ……………………10分
- +
极小值
∴ 当时,有最小值. ……………………12分
令, ∴,由,
∴ . ……………………14分
另解:,
当a=0时,,,函数在定义域上为增函数,与已知矛盾,舍;……………………7分
当a>0时,由(Ⅰ)知,,
函数在上为增函数,在上为减函数,与已知矛盾,舍;……………………8分
当a<0时,,由已知可得,∴ ……………9分
设, ………………10分
∴ 。
令,两个根为,,,
- +
极小值
∴ 当时,有最小值. ……………………12分
令, ∴,由,
∴ . ……………………14分
22.(本小题14分)
解:(Ⅰ)由已知,………………………………………(2分)
.故曲线在处切线的斜率为.……………(4分)
(Ⅱ).……………………………………………………(5分)
①当时,由于,故,
所以,的单调递增区间为.………………………………………(6分)
②当时,由,得.在区间上,,在区间上,
所以,函数的单调递增区间为,单调递减区间为.…(8分)
(Ⅲ)由已知,转化为.…………………………………………(9分)
……………………………………………………………………(10分)
由(Ⅱ)知,当时,在上单调递增,值域为,故不符合题意.
(或者举出反例:存在,故不符合题意.)……………(11分)
当时,在上单调递增,在上单调递减,
故的极大值即为最大值,,……(13分)
所以解得. ………………………………(14分)
……………………10分
……………………5分
……………………3分
……………………8分
名片管理系统
用户管理
用户登录
名片管理
出错信息处理
能修改密码
显示用户信息
修改用户信息
名片删除
名片添加
名片修改
名片查询
同课章节目录
