中考数学二轮专题《面积相关》
图片预览
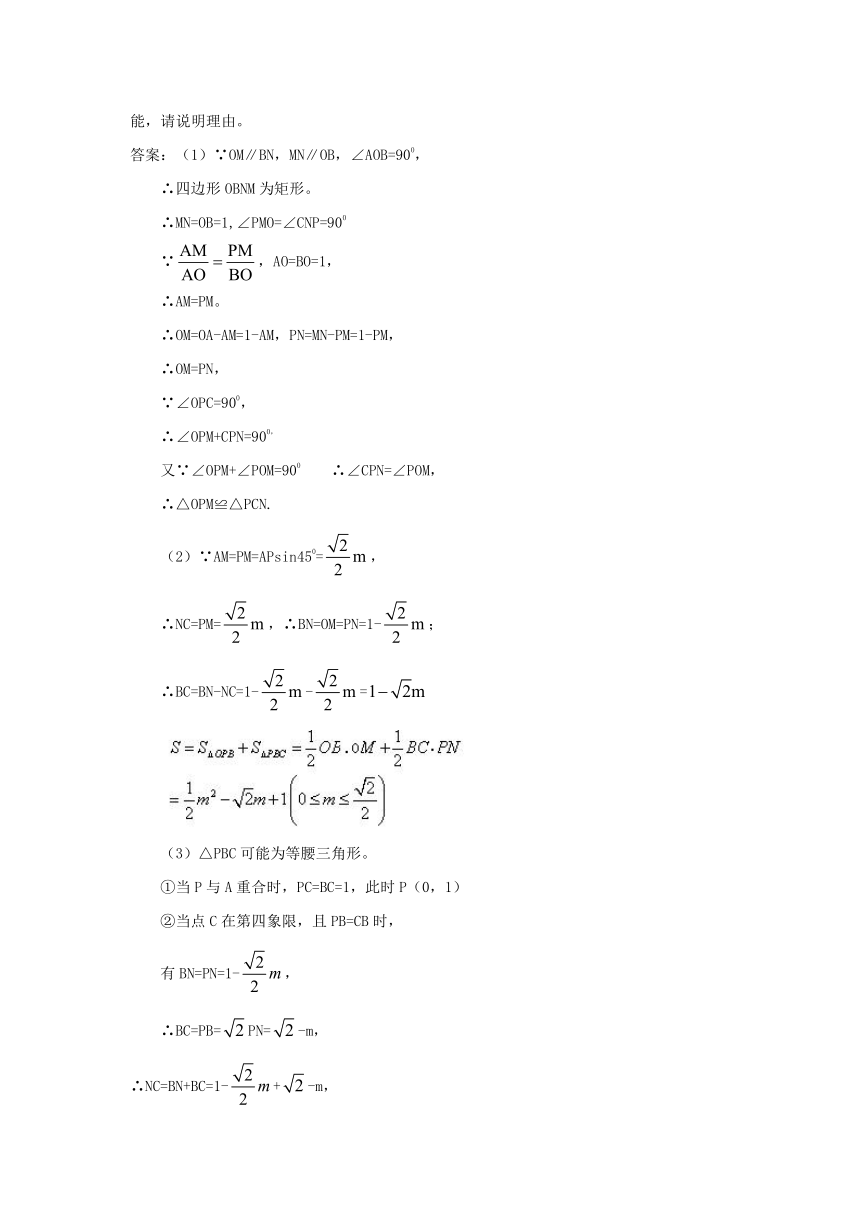

文档简介
课前测试:
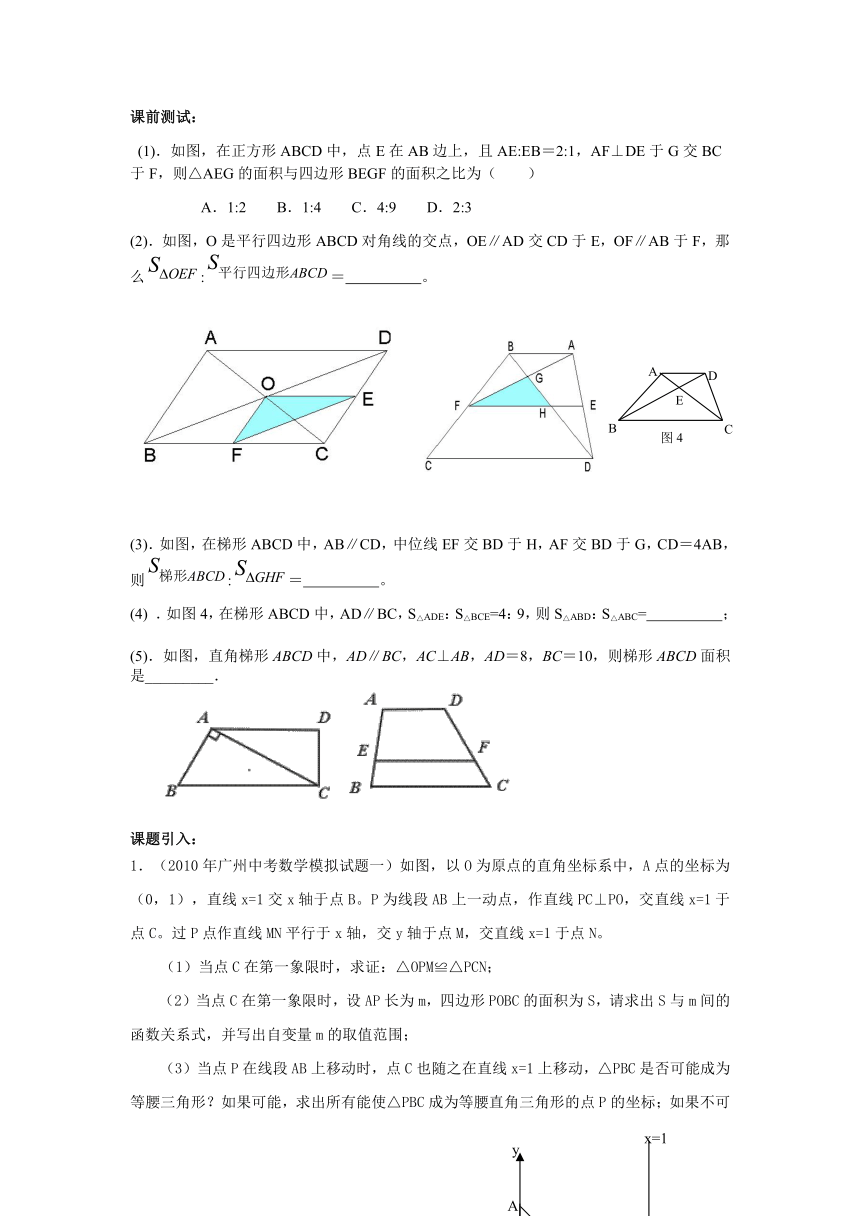
(1).如图,在正方形ABCD中,点E在AB边上,且AE:EB=2:1,AF⊥DE于G交BC于F,则△AEG的面积与四边形BEGF的面积之比为( )
A.1:2 B.1:4 C.4:9 D.2:3
(2).如图,O是平行四边形ABCD对角线的交点,OE∥AD交CD于E,OF∥AB于F,那么:= 。
.如图,在梯形ABCD中,AB∥CD,中位线EF交BD于H,AF交BD于G,CD=4AB,则:= 。
(4) .如图4,在梯形ABCD中,AD∥BC,S△ADE:S△BCE=4:9,则S△ABD:S△ABC= ;
(5).如图,直角梯形ABCD中,AD∥BC,AC⊥AB,AD=8,BC=10,则梯形ABCD面积是_________.
课题引入:
1.(2010年广州中考数学模拟试题一)如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B。P为线段AB上一动点,作直线PC⊥PO,交直线x=1于点C。过P点作直线MN平行于x轴,交y轴于点M,交直线x=1于点N。
(1)当点C在第一象限时,求证:△OPM≌△PCN;
(2)当点C在第一象限时,设AP长为m,四边形POBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围;
(3)当点P在线段AB上移动时,点C也随之在直线x=1上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰直角三角形的点P的坐标;如果不可能,请说明理由。
答案:(1)∵OM∥BN,MN∥OB,∠AOB=900,
∴四边形OBNM为矩形。
∴MN=OB=1,∠PMO=∠CNP=900
∵,AO=BO=1,
∴AM=PM。
∴OM=OA-AM=1-AM,PN=MN-PM=1-PM,
∴OM=PN,
∵∠OPC=900,
∴∠OPM+CPN=900,
又∵∠OPM+∠POM=900 ∴∠CPN=∠POM,
∴△OPM≌△PCN.
(2)∵AM=PM=APsin450=,
∴NC=PM=,∴BN=OM=PN=1-;
∴BC=BN-NC=1--=
(3)△PBC可能为等腰三角形。
①当P与A重合时,PC=BC=1,此时P(0,1)
②当点C在第四象限,且PB=CB时,
有BN=PN=1-,
∴BC=PB=PN=-m,
∴NC=BN+BC=1-+-m,
由⑵知:NC=PM=,
∴1-+-m=, ∴m=1.
∴PM==,BN=1-=1-,
∴P(,1-).
∴使△PBC为等腰三角形的的点P的坐标为(0,1)或(,1-)
2.(2011深圳20题)如图9,已知在⊙O中,点C为劣弧AB上的中点,连接AC并延长至D,使CD=CA,连接DB并延长交⊙O于点E,连接AE。
(1)求证:AE是⊙O的直径;
(2)如图10,连接EC,⊙O半径为5,AC的长为4,求阴影部分的面积之和。(结果保留π与根号)
(1)证明:如图2,连接AB、BC,
∵点C是劣弧AB上的中点
∴
∴CA=CB
又∵CD=CA
∴CB=CD=CA
∴在△ABD中,
∴∠ABD=90°
∴∠ABE=90°
∴AE是⊙O的直径
(2)解:如图3,由(1)可知,AE是⊙O的直径
∴∠ACE=90°
∵⊙O的半径为5,AC=4
∴AE=10,⊙O的面积为25π
在Rt△ACE中,∠ACE=90°,由勾股定理,得:
∴S△ACE=
∴S阴影=S⊙O-S△ACE=
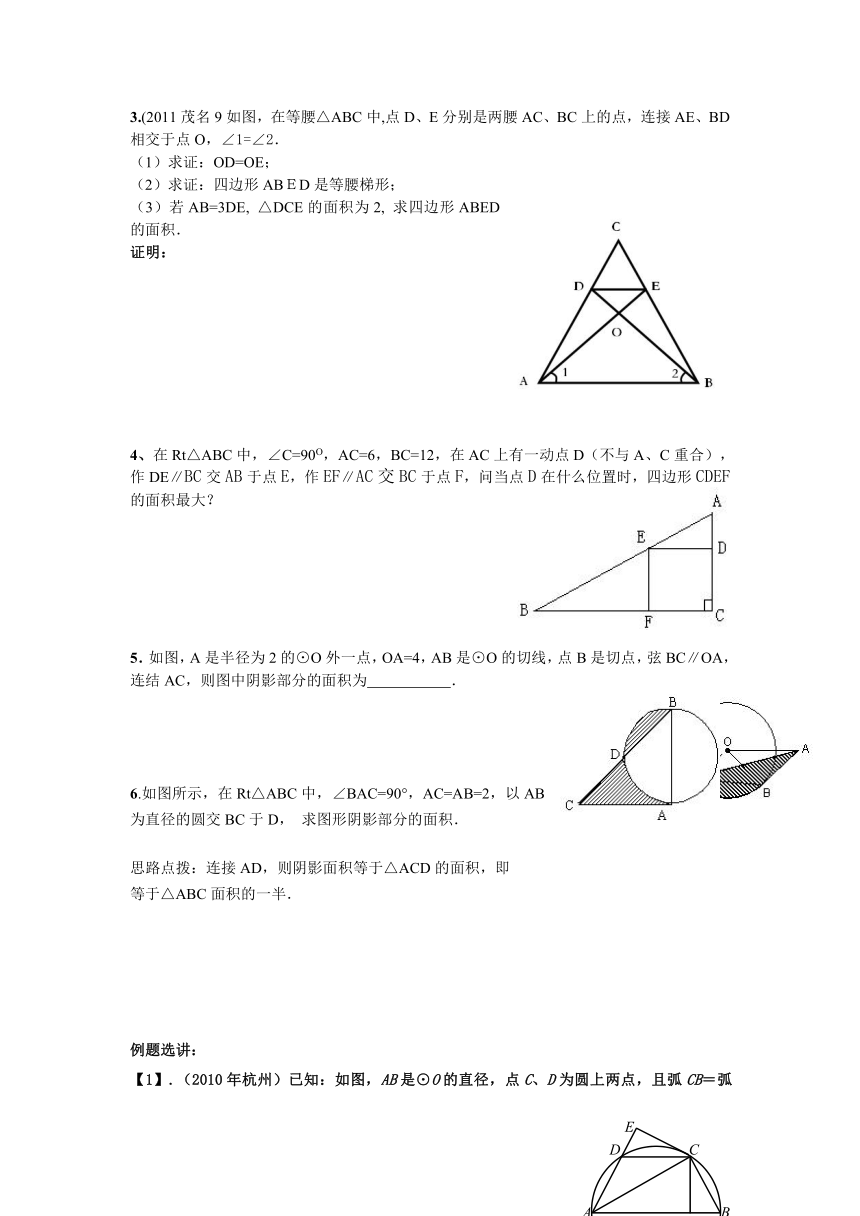
3.(2011茂名9如图,在等腰△ABC中,点D、E分别是两腰AC、BC上的点,连接AE、BD相交于点O,∠1=∠2.
(1)求证:OD=OE;
(2)求证:四边形ABED是等腰梯形;
(3)若AB=3DE, △DCE的面积为2, 求四边形ABED的面积.
证明:
4、在Rt△ABC中,∠C=90O,AC=6,BC=12,在AC上有一动点D(不与A、C重合),作DE∥BC交AB于点E,作EF∥AC交BC于点F,问当点D在什么位置时,四边形CDEF的面积最大?
5.如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,连结AC,则图中阴影部分的面积为 .
6.如图所示,在Rt△ABC中,∠BAC=90°,AC=AB=2,以AB为直径的圆交BC于D, 求图形阴影部分的面积.
思路点拨:连接AD,则阴影面积等于△ACD的面积,即等于△ABC面积的一半.
例题选讲:
【1】.(2010年杭州)已知:如图,AB是⊙O的直径,点C、D为圆上两点,且弧CB=弧CD,
CF⊥AB于点F,CE⊥AD的延长线于点E.
(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=6,求△ACD的面积.
(1)∵ 弧CB=弧CD ∴ CB=CD,∠CAE=∠CAB
又∵ CF⊥AB,CE⊥AD ∴ CE=CF ∴ △CED≌△CFB
∴ DE=BF (2)易得:△CAE≌△CAF
易求:
∴
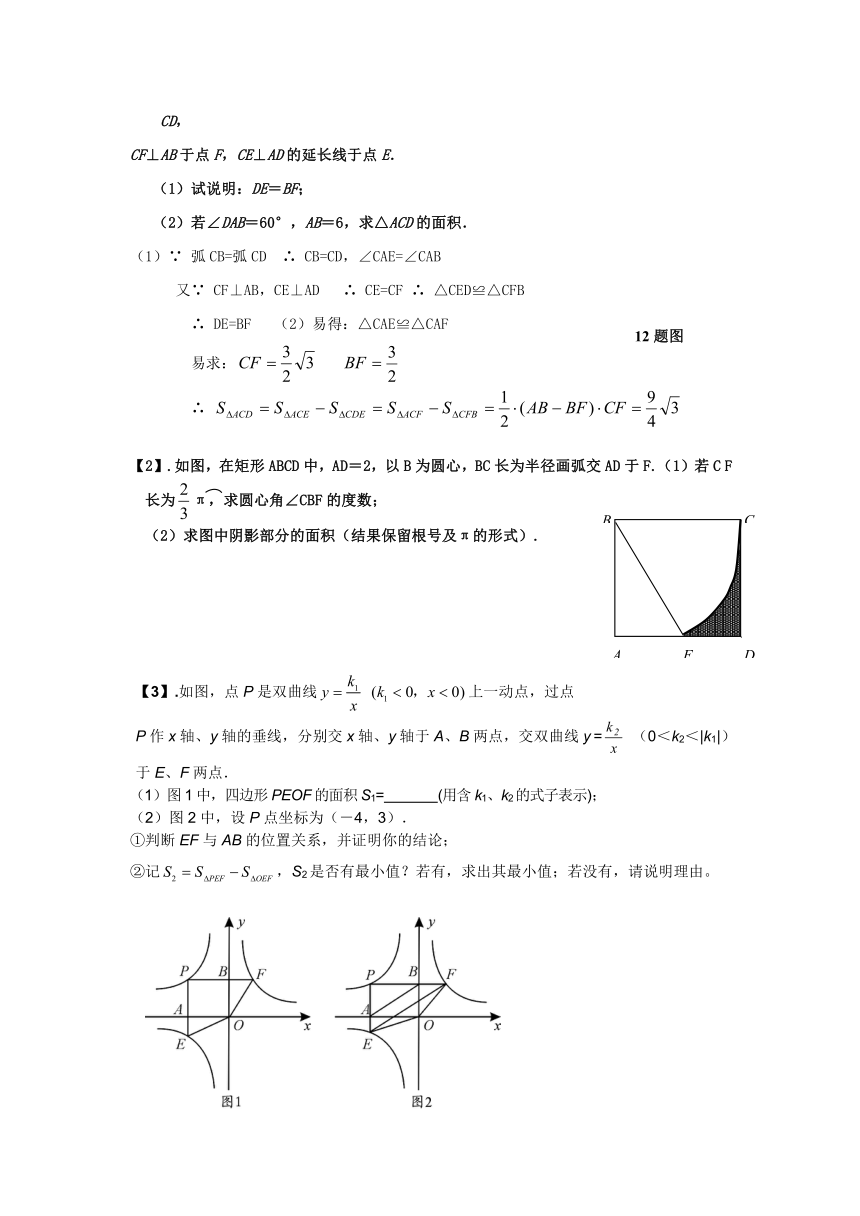
【2】.如图,在矩形ABCD中,AD=2,以B为圆心,BC长为半径画弧交AD于F.(1)若C F长为π,求圆心角∠CBF的度数;
(2)求图中阴影部分的面积(结果保留根号及π的形式).
【3】.如图,点P是双曲线上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交双曲线y= (0<k2<|k1|)于E、F两点.
(1)图1中,四边形PEOF的面积S1= (用含k1、k2的式子表示);
(2)图2中,设P点坐标为(-4,3).
①判断EF与AB的位置关系,并证明你的结论;
②记,S2是否有最小值?若有,求出其最小值;若没有,请说明理由。
【4】如图,直线与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为,正方形OCMD与△AOB重叠部分的面积为S.试求S与的函数关系式并画出该函数的图象.
【5】如图1,在△ABC中,∠C=90°,BC=8,AC=6,另有一直角梯形DEFH
(HF∥DE,∠HDE=90°)的底边DE落在CB上,腰DH落在CA上,且DE=4,∠DEF=∠CBA,AH∶AC=2∶3
(1)延长HF交AB于G,求△AHG的面积.
(2)操作:固定△ABC,将直角梯形DEFH以每秒1个
单位的速度沿CB方向向右移动,直到点D与点B
重合时停止,设运动的时间为t秒,运动后的直角梯
形为DEFH′(如图2).
探究1:在运动中,四边形CDH′H能否为正方形?若能, 请求出此时t的值;若不能,请说明理由.
探究2:在运动过程中,△ABC与直角梯形DEFH′重叠部分的面积为y,求y与t的函数关系.?
【6】如图,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及;
(3)是否存在一点P,使S△PAB=S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
【7】如图,已知抛物线与交于A(-1,0)、E(3,0)两点,与轴交于点B(0,3)。
求抛物线的解析式;
设抛物线顶点为D,求四边形AEDB的面积;
△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由。
【8】已知二次函数。
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点。
(2)设a<0,当此函数图象与x轴的两个交点的距离为时,求出此二次函数的解析式。
(3)若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为,若存在求出P点坐标,若不存在请说明理由。
【9】如图,已知射线DE与轴和轴分别交于点和点.动点从点出发,以1个单位长度/秒的速度沿轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动.设运动时间为秒.
(1)请用含的代数式分别表示出点C与点P的坐标;
(2)以点C为圆心、个单位长度为半径的与轴交于A、B两点(点A在点B的左侧),连接PA、PB.
①当与射线DE有公共点时,求的取值范围;
②当为等腰三角形时,求的值.
【10】已知直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3).
现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA
向终点A运动,设运动时间为t秒.
(1)填空:菱形ABCD的边长是 ▲ 、面积是 ▲ 、 高BE的长是 ▲ ;
(2)探究下列问题:
①若点P的速度为每秒1个单位,点Q的速度为每秒2个单位.当点Q在线段BA上时,求△APQ的面积S关于t的函数关系式,以及S的最大值;
②若点P的速度为每秒1个单位,点Q的速度变为每秒k个单位,在运动过程中,任何时刻都有相应的k值,使得△APQ沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形.请探究当t=4秒时的情形,并求出k的值。
【11】如图,已知A、B是线段MN上的两点,,,.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设.
(1)求x的取值范围;
(2)若△ABC为直角三角形,求x的值;
(3)探究:△ABC的最大面积?
【12】已知抛物线()与轴相交于点,顶点为.直线分别与轴,轴相交于两点,并且与直线相交于点.
(1)填空:试用含的代数式分别表示点与的坐标,则;
(2)如图a,将沿轴翻折,若点的对应点′恰好落在抛物线上,′与轴交于点,连结,求的值和四边形的面积;
(3)在抛物线()上是否存在一点,使得以为顶点的四边形是平行四边形?若存在,求出点的坐标;若不存在,试说明理由.
【13】如图①,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),
点C在第一象限.动点P在正方形 ABCD的边上,从点A出发沿A→B→C→D匀速运动,
同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,
设运动的时间为t秒.
(1)当P点在边AB上运动时,点Q的横坐标(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;
(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相
等,若能,写出所有符合条件的t的值;若不能,请说明理由.
【14】已知:如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3.过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.
(1)求过点E、D、C的抛物线的解析式;
(2)将∠EDC绕点D按顺时针方向旋转后,角的一边与y轴的正半轴交于点F,另一边与线段OC交于点G.如果DF与(1)中的抛物线交于另一点M,点M的横坐标为,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
【15】已知平行于x轴的直线与函数和函数的图像分别交于点A和点B,又有定点P(2,0) .
(1)若,且tan∠POB=,求线段AB的长;
(2)在过A,B两点且顶点在直线上的抛物线中,已知线段AB=,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
(3)已知经过A,B,P三点的抛物线,平移后能得到的图像,求点P到直线AB的距离。
【16】如图1,在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),将四边形OABC绕点O按顺时针方向旋转α度得到四边形OA′B′C′,此时声母OA′、直线B′C′分别与直线BC相交于P、Q.
(1)四边形的形状是 , 当α=90°时,的值是 .
(2)①如图2,当四边形OA′B′C′的顶点B′落在y轴正半轴上时,求的值;
②如图3,当四边形OA′B′C′的顶点B′落在直线BC上时,求ΔOPB′的面积.
(3)在四边形OABC旋转过程中,当时,是否存在这样的点P和点Q,使BP=?若存在,请直接写出点P的坐标;基不存在,请说明理由.
【17】如图,已知点A(-4,8)和点B(2,n)在抛物线上.
(1) 求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
(2) 平移抛物线,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
① 当抛物线向左平移到某个位置时,A′C+CB′ 最短,求此时抛物线的函数解析式;
② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A′B′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
【18】△与△是两个直角边都等于厘米的等腰直角三角形,M、N分别是直角边AC、BC的中点。△位置固定,△按如图叠放,使斜边在直线MN上,顶点与点M重合。等腰直角△以1厘米/秒的速度沿直线MN向右平移,直到点与点N重合。设秒时,△与△重叠部分面积为平方厘米。
(1)当△与△重叠部分面积为平方厘米时,求△移动的时间;
(2)求与的函数关系式;
(3)求△与△重叠部分面积的最大值。
A
B
C
D
E
图4
A
B
C
N
P
M
O
x
y
x=1
第1题图
O
A
E
C
B
D
图10
O
A
E
C
B
D
图9
O
A
E
C
B
D
图2
O
A
E
C
B
D
图3
A B
O F
E
D C
12题图
B
C
A
F
D
(第25题图)
B
x
y
M
C
D
O
A
图(1)
B
x
y
O
A
图(2)
B
x
y
O
A
图(3)
图2
图1
(第27题图)
x
C
O
y
A
B
D
1
1
O
x
y
E
P
D
A
B
M
C
C
A
B
N
M
图a
x
y
B
C
O
D
A
M
N
N′
x
y
B
C
O
A
M
N
备用图
(第36题图)
y
x
D
B
C
A
E
E
O
(第37题图)
(第39题图)
4
x
2
2
A
8
-2
O
-2
-4
y
6
B
C
D
-4
4
(1).如图,在正方形ABCD中,点E在AB边上,且AE:EB=2:1,AF⊥DE于G交BC于F,则△AEG的面积与四边形BEGF的面积之比为( )
A.1:2 B.1:4 C.4:9 D.2:3
(2).如图,O是平行四边形ABCD对角线的交点,OE∥AD交CD于E,OF∥AB于F,那么:= 。
.如图,在梯形ABCD中,AB∥CD,中位线EF交BD于H,AF交BD于G,CD=4AB,则:= 。
(4) .如图4,在梯形ABCD中,AD∥BC,S△ADE:S△BCE=4:9,则S△ABD:S△ABC= ;
(5).如图,直角梯形ABCD中,AD∥BC,AC⊥AB,AD=8,BC=10,则梯形ABCD面积是_________.
课题引入:
1.(2010年广州中考数学模拟试题一)如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B。P为线段AB上一动点,作直线PC⊥PO,交直线x=1于点C。过P点作直线MN平行于x轴,交y轴于点M,交直线x=1于点N。
(1)当点C在第一象限时,求证:△OPM≌△PCN;
(2)当点C在第一象限时,设AP长为m,四边形POBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围;
(3)当点P在线段AB上移动时,点C也随之在直线x=1上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰直角三角形的点P的坐标;如果不可能,请说明理由。
答案:(1)∵OM∥BN,MN∥OB,∠AOB=900,
∴四边形OBNM为矩形。
∴MN=OB=1,∠PMO=∠CNP=900
∵,AO=BO=1,
∴AM=PM。
∴OM=OA-AM=1-AM,PN=MN-PM=1-PM,
∴OM=PN,
∵∠OPC=900,
∴∠OPM+CPN=900,
又∵∠OPM+∠POM=900 ∴∠CPN=∠POM,
∴△OPM≌△PCN.
(2)∵AM=PM=APsin450=,
∴NC=PM=,∴BN=OM=PN=1-;
∴BC=BN-NC=1--=
(3)△PBC可能为等腰三角形。
①当P与A重合时,PC=BC=1,此时P(0,1)
②当点C在第四象限,且PB=CB时,
有BN=PN=1-,
∴BC=PB=PN=-m,
∴NC=BN+BC=1-+-m,
由⑵知:NC=PM=,
∴1-+-m=, ∴m=1.
∴PM==,BN=1-=1-,
∴P(,1-).
∴使△PBC为等腰三角形的的点P的坐标为(0,1)或(,1-)
2.(2011深圳20题)如图9,已知在⊙O中,点C为劣弧AB上的中点,连接AC并延长至D,使CD=CA,连接DB并延长交⊙O于点E,连接AE。
(1)求证:AE是⊙O的直径;
(2)如图10,连接EC,⊙O半径为5,AC的长为4,求阴影部分的面积之和。(结果保留π与根号)
(1)证明:如图2,连接AB、BC,
∵点C是劣弧AB上的中点
∴
∴CA=CB
又∵CD=CA
∴CB=CD=CA
∴在△ABD中,
∴∠ABD=90°
∴∠ABE=90°
∴AE是⊙O的直径
(2)解:如图3,由(1)可知,AE是⊙O的直径
∴∠ACE=90°
∵⊙O的半径为5,AC=4
∴AE=10,⊙O的面积为25π
在Rt△ACE中,∠ACE=90°,由勾股定理,得:
∴S△ACE=
∴S阴影=S⊙O-S△ACE=
3.(2011茂名9如图,在等腰△ABC中,点D、E分别是两腰AC、BC上的点,连接AE、BD相交于点O,∠1=∠2.
(1)求证:OD=OE;
(2)求证:四边形ABED是等腰梯形;
(3)若AB=3DE, △DCE的面积为2, 求四边形ABED的面积.
证明:
4、在Rt△ABC中,∠C=90O,AC=6,BC=12,在AC上有一动点D(不与A、C重合),作DE∥BC交AB于点E,作EF∥AC交BC于点F,问当点D在什么位置时,四边形CDEF的面积最大?
5.如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,连结AC,则图中阴影部分的面积为 .
6.如图所示,在Rt△ABC中,∠BAC=90°,AC=AB=2,以AB为直径的圆交BC于D, 求图形阴影部分的面积.
思路点拨:连接AD,则阴影面积等于△ACD的面积,即等于△ABC面积的一半.
例题选讲:
【1】.(2010年杭州)已知:如图,AB是⊙O的直径,点C、D为圆上两点,且弧CB=弧CD,
CF⊥AB于点F,CE⊥AD的延长线于点E.
(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=6,求△ACD的面积.
(1)∵ 弧CB=弧CD ∴ CB=CD,∠CAE=∠CAB
又∵ CF⊥AB,CE⊥AD ∴ CE=CF ∴ △CED≌△CFB
∴ DE=BF (2)易得:△CAE≌△CAF
易求:
∴
【2】.如图,在矩形ABCD中,AD=2,以B为圆心,BC长为半径画弧交AD于F.(1)若C F长为π,求圆心角∠CBF的度数;
(2)求图中阴影部分的面积(结果保留根号及π的形式).
【3】.如图,点P是双曲线上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交双曲线y= (0<k2<|k1|)于E、F两点.
(1)图1中,四边形PEOF的面积S1= (用含k1、k2的式子表示);
(2)图2中,设P点坐标为(-4,3).
①判断EF与AB的位置关系,并证明你的结论;
②记,S2是否有最小值?若有,求出其最小值;若没有,请说明理由。
【4】如图,直线与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为,正方形OCMD与△AOB重叠部分的面积为S.试求S与的函数关系式并画出该函数的图象.
【5】如图1,在△ABC中,∠C=90°,BC=8,AC=6,另有一直角梯形DEFH
(HF∥DE,∠HDE=90°)的底边DE落在CB上,腰DH落在CA上,且DE=4,∠DEF=∠CBA,AH∶AC=2∶3
(1)延长HF交AB于G,求△AHG的面积.
(2)操作:固定△ABC,将直角梯形DEFH以每秒1个
单位的速度沿CB方向向右移动,直到点D与点B
重合时停止,设运动的时间为t秒,运动后的直角梯
形为DEFH′(如图2).
探究1:在运动中,四边形CDH′H能否为正方形?若能, 请求出此时t的值;若不能,请说明理由.
探究2:在运动过程中,△ABC与直角梯形DEFH′重叠部分的面积为y,求y与t的函数关系.?
【6】如图,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及;
(3)是否存在一点P,使S△PAB=S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
【7】如图,已知抛物线与交于A(-1,0)、E(3,0)两点,与轴交于点B(0,3)。
求抛物线的解析式;
设抛物线顶点为D,求四边形AEDB的面积;
△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由。
【8】已知二次函数。
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点。
(2)设a<0,当此函数图象与x轴的两个交点的距离为时,求出此二次函数的解析式。
(3)若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为,若存在求出P点坐标,若不存在请说明理由。
【9】如图,已知射线DE与轴和轴分别交于点和点.动点从点出发,以1个单位长度/秒的速度沿轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动.设运动时间为秒.
(1)请用含的代数式分别表示出点C与点P的坐标;
(2)以点C为圆心、个单位长度为半径的与轴交于A、B两点(点A在点B的左侧),连接PA、PB.
①当与射线DE有公共点时,求的取值范围;
②当为等腰三角形时,求的值.
【10】已知直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3).
现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA
向终点A运动,设运动时间为t秒.
(1)填空:菱形ABCD的边长是 ▲ 、面积是 ▲ 、 高BE的长是 ▲ ;
(2)探究下列问题:
①若点P的速度为每秒1个单位,点Q的速度为每秒2个单位.当点Q在线段BA上时,求△APQ的面积S关于t的函数关系式,以及S的最大值;
②若点P的速度为每秒1个单位,点Q的速度变为每秒k个单位,在运动过程中,任何时刻都有相应的k值,使得△APQ沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形.请探究当t=4秒时的情形,并求出k的值。
【11】如图,已知A、B是线段MN上的两点,,,.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设.
(1)求x的取值范围;
(2)若△ABC为直角三角形,求x的值;
(3)探究:△ABC的最大面积?
【12】已知抛物线()与轴相交于点,顶点为.直线分别与轴,轴相交于两点,并且与直线相交于点.
(1)填空:试用含的代数式分别表示点与的坐标,则;
(2)如图a,将沿轴翻折,若点的对应点′恰好落在抛物线上,′与轴交于点,连结,求的值和四边形的面积;
(3)在抛物线()上是否存在一点,使得以为顶点的四边形是平行四边形?若存在,求出点的坐标;若不存在,试说明理由.
【13】如图①,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),
点C在第一象限.动点P在正方形 ABCD的边上,从点A出发沿A→B→C→D匀速运动,
同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,
设运动的时间为t秒.
(1)当P点在边AB上运动时,点Q的横坐标(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;
(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相
等,若能,写出所有符合条件的t的值;若不能,请说明理由.
【14】已知:如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3.过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.
(1)求过点E、D、C的抛物线的解析式;
(2)将∠EDC绕点D按顺时针方向旋转后,角的一边与y轴的正半轴交于点F,另一边与线段OC交于点G.如果DF与(1)中的抛物线交于另一点M,点M的横坐标为,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
【15】已知平行于x轴的直线与函数和函数的图像分别交于点A和点B,又有定点P(2,0) .
(1)若,且tan∠POB=,求线段AB的长;
(2)在过A,B两点且顶点在直线上的抛物线中,已知线段AB=,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
(3)已知经过A,B,P三点的抛物线,平移后能得到的图像,求点P到直线AB的距离。
【16】如图1,在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),将四边形OABC绕点O按顺时针方向旋转α度得到四边形OA′B′C′,此时声母OA′、直线B′C′分别与直线BC相交于P、Q.
(1)四边形的形状是 , 当α=90°时,的值是 .
(2)①如图2,当四边形OA′B′C′的顶点B′落在y轴正半轴上时,求的值;
②如图3,当四边形OA′B′C′的顶点B′落在直线BC上时,求ΔOPB′的面积.
(3)在四边形OABC旋转过程中,当时,是否存在这样的点P和点Q,使BP=?若存在,请直接写出点P的坐标;基不存在,请说明理由.
【17】如图,已知点A(-4,8)和点B(2,n)在抛物线上.
(1) 求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
(2) 平移抛物线,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
① 当抛物线向左平移到某个位置时,A′C+CB′ 最短,求此时抛物线的函数解析式;
② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A′B′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
【18】△与△是两个直角边都等于厘米的等腰直角三角形,M、N分别是直角边AC、BC的中点。△位置固定,△按如图叠放,使斜边在直线MN上,顶点与点M重合。等腰直角△以1厘米/秒的速度沿直线MN向右平移,直到点与点N重合。设秒时,△与△重叠部分面积为平方厘米。
(1)当△与△重叠部分面积为平方厘米时,求△移动的时间;
(2)求与的函数关系式;
(3)求△与△重叠部分面积的最大值。
A
B
C
D
E
图4
A
B
C
N
P
M
O
x
y
x=1
第1题图
O
A
E
C
B
D
图10
O
A
E
C
B
D
图9
O
A
E
C
B
D
图2
O
A
E
C
B
D
图3
A B
O F
E
D C
12题图
B
C
A
F
D
(第25题图)
B
x
y
M
C
D
O
A
图(1)
B
x
y
O
A
图(2)
B
x
y
O
A
图(3)
图2
图1
(第27题图)
x
C
O
y
A
B
D
1
1
O
x
y
E
P
D
A
B
M
C
C
A
B
N
M
图a
x
y
B
C
O
D
A
M
N
N′
x
y
B
C
O
A
M
N
备用图
(第36题图)
y
x
D
B
C
A
E
E
O
(第37题图)
(第39题图)
4
x
2
2
A
8
-2
O
-2
-4
y
6
B
C
D
-4
4
同课章节目录
