11.4《互逆命题(2)》课件(苏科版八年级下)(12张)
文档属性
| 名称 | 11.4《互逆命题(2)》课件(苏科版八年级下)(12张) |

|
|
| 格式 | zip | ||
| 文件大小 | 17.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-18 00:00:00 | ||
图片预览


文档简介
(共12张PPT)
初中数学八年级下册
(苏科版)
11.4 互逆命题(2)
情境一
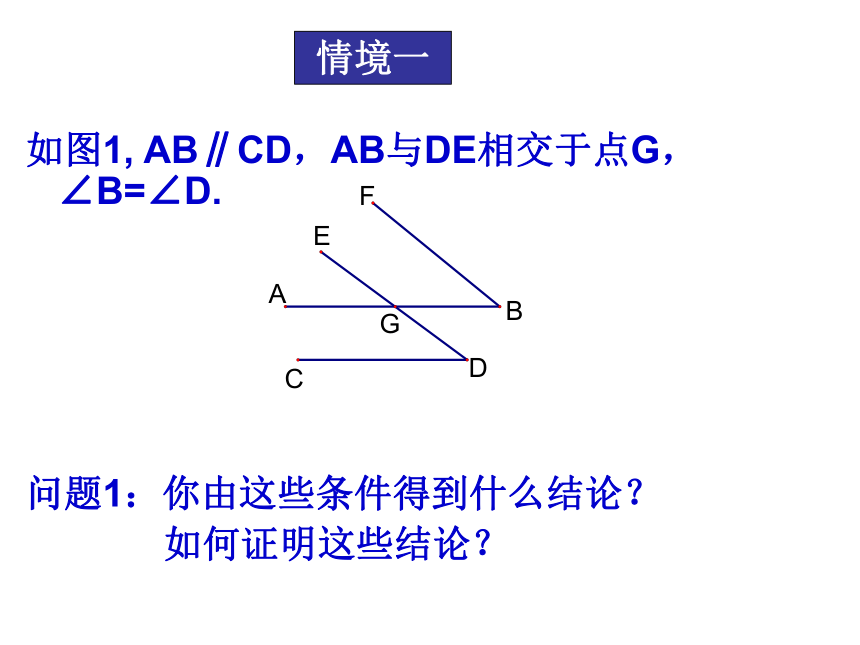
如图1, AB∥CD,AB与DE相交于点G,∠B=∠D.
问题1:你由这些条件得到什么结论?
如何证明这些结论?
交流一
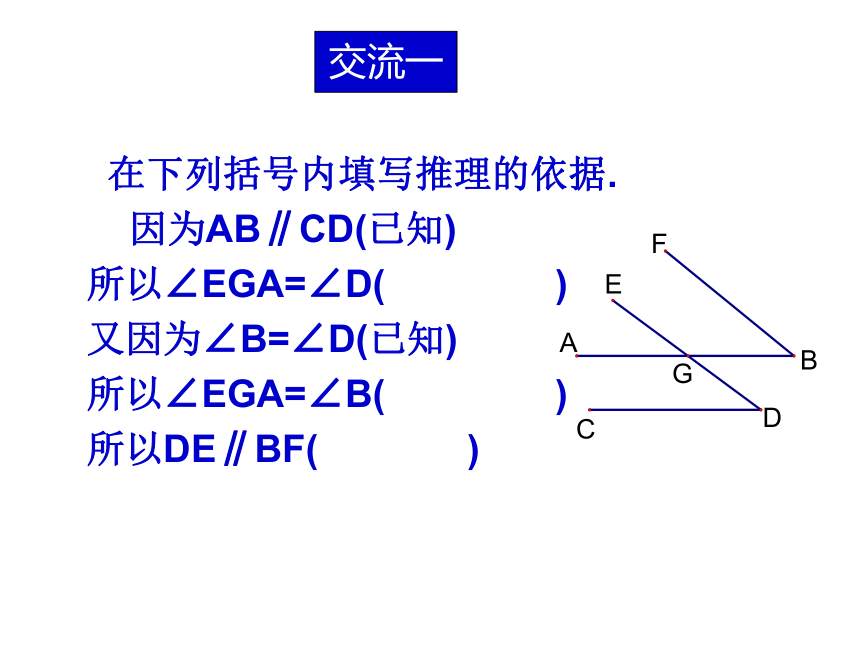
在下列括号内填写推理的依据.
因为AB∥CD(已知)
所以∠EGA=∠D( )
又因为∠B=∠D(已知)
所以∠EGA=∠B( )
所以DE∥BF( )
交流二
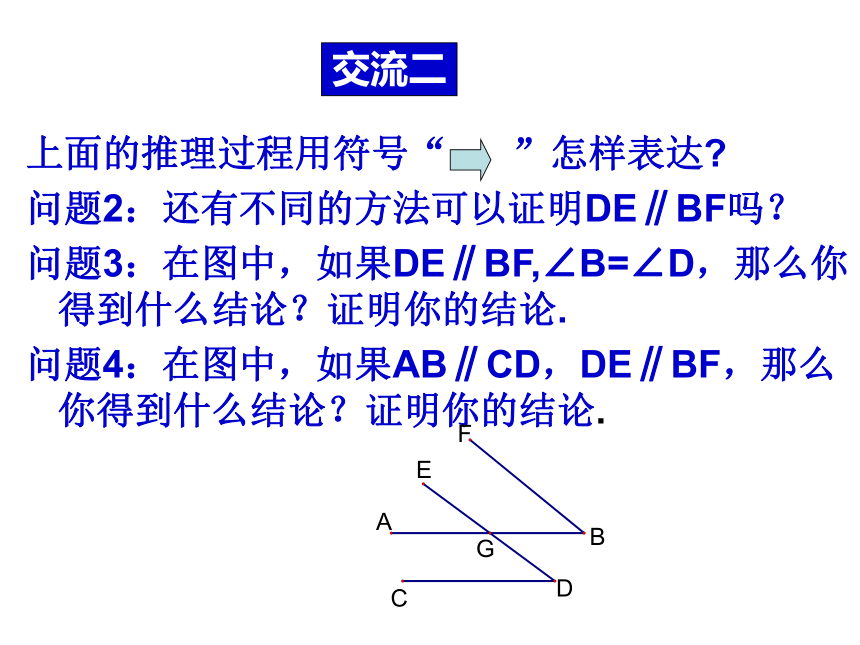
上面的推理过程用符号“ ”怎样表达
问题2:还有不同的方法可以证明DE∥BF吗?
问题3:在图中,如果DE∥BF,∠B=∠D,那么你得到什么结论?证明你的结论.
问题4:在图中,如果AB∥CD,DE∥BF,那么你得到什么结论?证明你的结论.
例题精讲
证明:如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
分 析
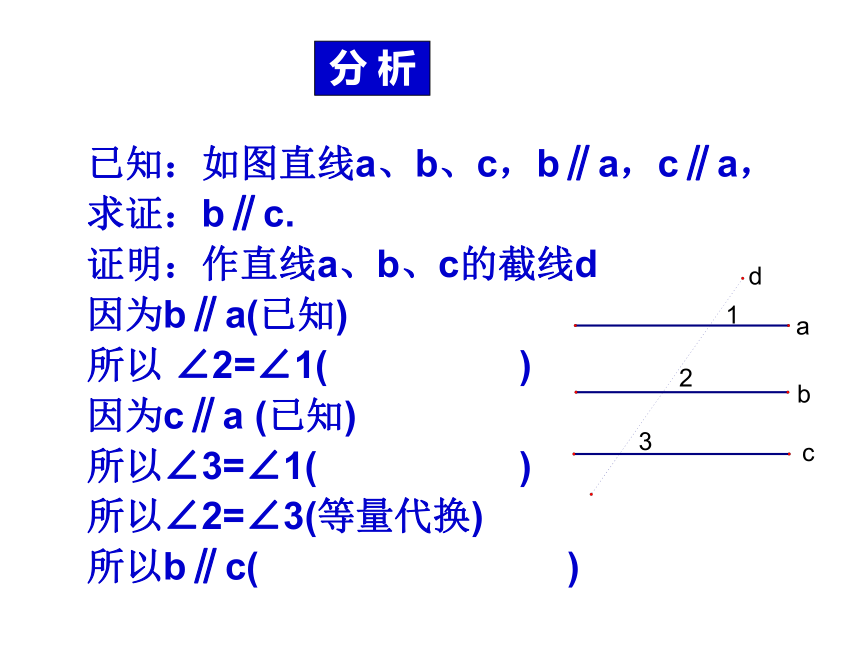
已知:如图直线a、b、c,b∥a,c∥a,
求证:b∥c.
证明:作直线a、b、c的截线d
因为b∥a(已知)
所以 ∠2=∠1( )
因为c∥a (已知)
所以∠3=∠1( )
所以∠2=∠3(等量代换)
所以b∥c( )
交 流 三
1.用符号“ ”简明表述上述的推理过程.
b∥a ∠2=∠1
∠2=∠3 b∥c
c∥a ∠3=∠1
2.你还有其他的方法
证明b∥c吗?
例题精讲
例2 如图,△ABC中,AB=AC,D在BC上,且BD=AD,DC=AC,求∠B的度数.
分析:
图中有三个等腰三角形,
可用等边对等角的性质,
再用方程的思想解题,
列方程的依据是
三角形内角和定理.
解:∵AB=AC(已知)
∴∠B=∠C(等边对等角)
同理,∠B=∠BAD,∠CAD=∠CDA.
设∠B=x°,则∠C=x°,∠BAD=x°,∴∠ADC=2x°, ∠CAD=2x°.
在△ADC中,∵∠C+∠CAD+∠ADC=180°.
∴x°+2 x°+ 2x°=180 °.
∴x°=36 °.
答:∠B的度数为36°.
例 题 精 讲
拓 展 练 习
1.给下面的证明过程证明理由
已知AB=DC,∠BAD=∠CDA
求证:∠ABC=∠DCB
证明:连结AC、BD交点为O
在△ADB与△DAC中
因为∠BAD=∠ADC( )
AD=DA( )
AB=DC( )
所以△ADB≌△DAC( )
所以BD=CA 又在△ABC与△DCB中
因为BD=CA( ) AB=DC( ) BC=BC( )
所以△ABC≌△DCB( )
所以∠ABC=∠DCB
拓 展 练 习
2. 证明:等角的余角相等.
本节课你学到什么?
收 获
初中数学八年级下册
(苏科版)
11.4 互逆命题(2)
情境一
如图1, AB∥CD,AB与DE相交于点G,∠B=∠D.
问题1:你由这些条件得到什么结论?
如何证明这些结论?
交流一
在下列括号内填写推理的依据.
因为AB∥CD(已知)
所以∠EGA=∠D( )
又因为∠B=∠D(已知)
所以∠EGA=∠B( )
所以DE∥BF( )
交流二
上面的推理过程用符号“ ”怎样表达
问题2:还有不同的方法可以证明DE∥BF吗?
问题3:在图中,如果DE∥BF,∠B=∠D,那么你得到什么结论?证明你的结论.
问题4:在图中,如果AB∥CD,DE∥BF,那么你得到什么结论?证明你的结论.
例题精讲
证明:如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
分 析
已知:如图直线a、b、c,b∥a,c∥a,
求证:b∥c.
证明:作直线a、b、c的截线d
因为b∥a(已知)
所以 ∠2=∠1( )
因为c∥a (已知)
所以∠3=∠1( )
所以∠2=∠3(等量代换)
所以b∥c( )
交 流 三
1.用符号“ ”简明表述上述的推理过程.
b∥a ∠2=∠1
∠2=∠3 b∥c
c∥a ∠3=∠1
2.你还有其他的方法
证明b∥c吗?
例题精讲
例2 如图,△ABC中,AB=AC,D在BC上,且BD=AD,DC=AC,求∠B的度数.
分析:
图中有三个等腰三角形,
可用等边对等角的性质,
再用方程的思想解题,
列方程的依据是
三角形内角和定理.
解:∵AB=AC(已知)
∴∠B=∠C(等边对等角)
同理,∠B=∠BAD,∠CAD=∠CDA.
设∠B=x°,则∠C=x°,∠BAD=x°,∴∠ADC=2x°, ∠CAD=2x°.
在△ADC中,∵∠C+∠CAD+∠ADC=180°.
∴x°+2 x°+ 2x°=180 °.
∴x°=36 °.
答:∠B的度数为36°.
例 题 精 讲
拓 展 练 习
1.给下面的证明过程证明理由
已知AB=DC,∠BAD=∠CDA
求证:∠ABC=∠DCB
证明:连结AC、BD交点为O
在△ADB与△DAC中
因为∠BAD=∠ADC( )
AD=DA( )
AB=DC( )
所以△ADB≌△DAC( )
所以BD=CA 又在△ABC与△DCB中
因为BD=CA( ) AB=DC( ) BC=BC( )
所以△ABC≌△DCB( )
所以∠ABC=∠DCB
拓 展 练 习
2. 证明:等角的余角相等.
本节课你学到什么?
收 获
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
