11.3《证明（3）》

(共14张PPT)
初中数学八年级下册
（苏科版）
11.3 证明（3）
你知道吗？
180°
三角形3个内角的和是 .
°
探索发现
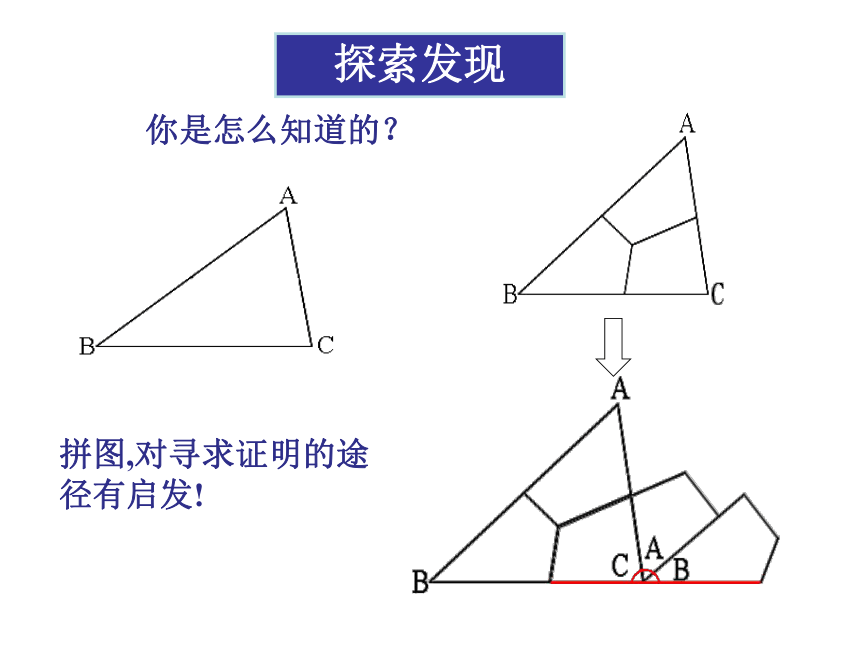
你是怎么知道的？
拼图,对寻求证明的途径有启发!
探索发现
如何证明三角形内角和等于180°？
探索发现
A
B
C
1
2
D
E
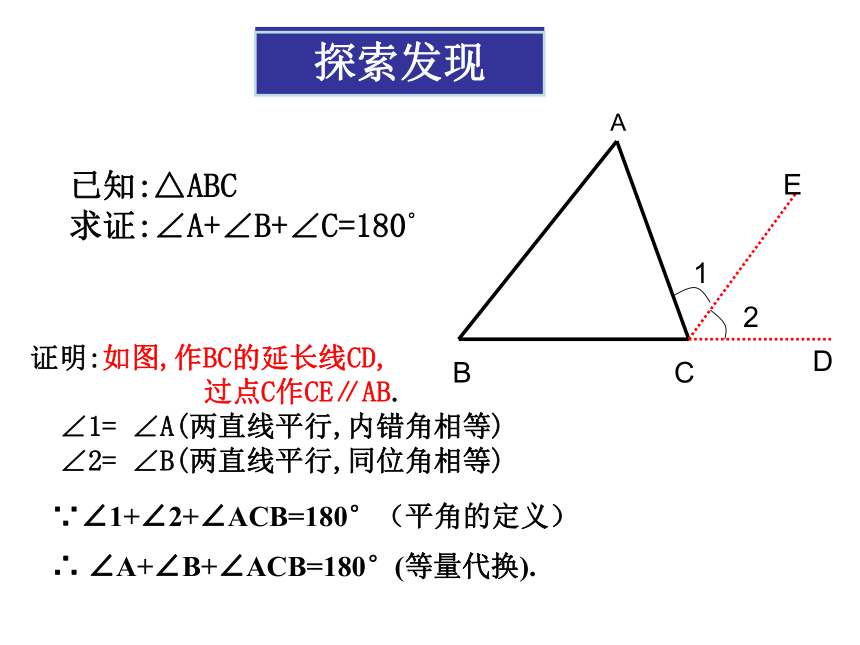
已知:△ABC
求证:∠A+∠B+∠C=180°
证明:如图,作BC的延长线CD,
过点C作CE∥AB.
∠1= ∠A(两直线平行,内错角相等)
∠2= ∠B(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°（平角的定义）
∴ ∠A+∠B+∠ACB=180°(等量代换).
探索发现
探索发现
A
B
C
E
D
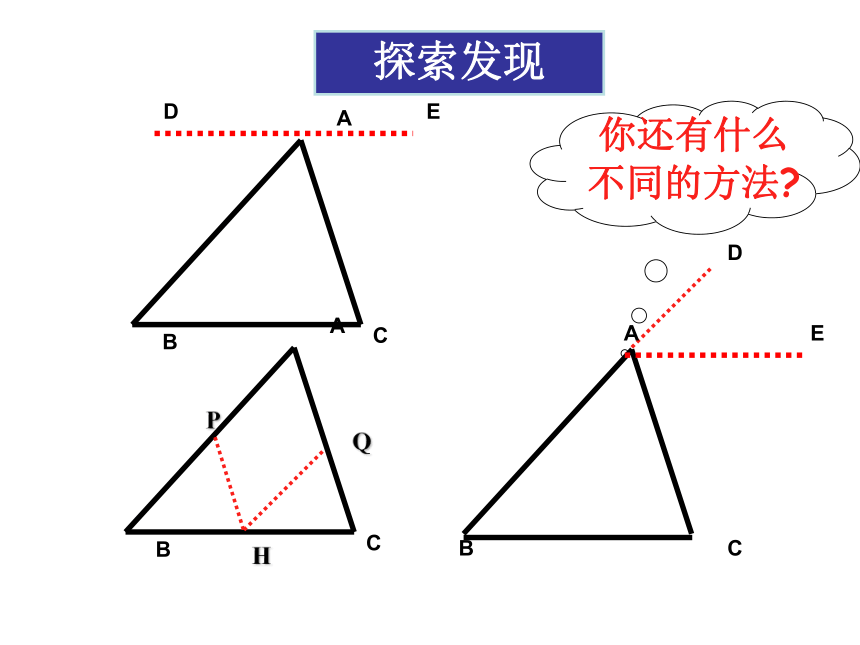
你还有什么
不同的方法
A
B
C
P
H
Q
E
B
C
D
A
探索发现
关于辅助线
1.辅助线是为了证明需要在原图上添画的
线.（辅助线通常画成虚线）
2.它的作用是把分散的条件集中，把隐含
的条件显现出来，起到牵线搭桥的作用.
3.添加辅助线，可构造新图形，形成新关系，找到联系已知与未知的桥梁，把问题
转化，但辅助线的添法没有一定的规律，
要根据需要而定,平时做题时要注意总结.
三角形内角和定理 ：
三角形三个内角的和等于180°。
归纳总结
如图，∠α是△ABC的一个外角，∠α与△ABC的内角有怎样的大小关系？
由三角形内角和定理，可以知道：∠α=∠A+∠B
三角形内角和定理的推论：
1.三角形的一个外角等于和它不相邻的两个内角的和；
2.三角形的一个外角大于任何一个和它不相邻的内角.
进而， ∠α>∠A， ∠α >∠B.
α
C
B
A
γ
β
探索发现
1. 证明：直角三角形两个锐角互余。
求证：∠A＋∠B＝90°
已知：如图，△ABC中，∠C=90°
证明:∵∠A＋∠B＋∠C=180°(三角形的
内角和定理)
∴ ∠A＋∠B=180°-∠C
又∵ ∠C=90°
∴ ∠A＋∠B=180°- 90°= 90°
课堂练习
2 . 如图，∠α、∠β、∠γ是△ABC的3个外角；
猜想△ABC的3个外角的和是多少？证明你的猜想。
解： ∠α+ ∠β+ ∠γ=360°
∵ ∠1+ ∠α=180° ∠2+ ∠β=180°
∠ 3+ ∠γ= 180 (平角的定义)
∴∠1+ ∠α+∠2+ ∠β+ ∠3+ ∠γ=540°
∴ ∠α+ ∠β+ ∠γ =540°- (∠1 +∠2+ ∠3)
= 540°- 180°
= 360°
γ
β
C
B
A
α
⌒
1
⌒
2
3
⌒
课堂练习
3、四边形的内角和等于多少度？证明你的结论.
已知：四边形ABCD
求证：∠A+∠B+∠C+∠D=360°.
证明:
连接AC
∵∠1+∠2+∠D=180°
∠ 3+∠4+∠B=180°(三角形的内角和定理)
A
B
C
D
⌒
⌒
⌒
2
⌒
1
3
4
∴∠1+∠2+∠D+∠3+∠4+∠B=360°
又∵ ∠DAB=∠1+∠3 ∠DCB=∠2+∠4
∴ ∠DAB+ ∠B+ ∠DCB+∠D= 360°(等量代换)
即四边形的内角和等于360°
课堂练习
通过这节课的学习,你有哪些收获？
1.我们通过添加辅助线,把三角形的3个内角拼成1个平角;把三角形的3个内角拼成两平行线的同旁内角,证明了三角形内角和定理及推论.
2.继续感受数学的严谨、结论的确定，初步养成言之有理、落笔有据的推理习惯，发展初步的演绎推理能力.
课堂小结
已知:如图，D是△ ABC内的任意一点.
求证: ∠BDC= ∠1+ ∠A+ ∠ 2
A
B
D
C
Q
⌒
⌒
1
2
课后练习