探索三角形全等的条件-习题课

5.4.4 探索三角形全等的条件_习题课
一、热身：
1.判断：（若正确，请写出这是哪种判定方法，并归纳共有哪几种说明三角形全等的方法）
（1）若有三组边对应相等，则两个三角形全等（ ）
（2）若有三组角对应相等，则两个三角形全等（ ）
（3）若有两组角对应相等，还有一组边对应相等，则两个三角形全等（ ）
（4）若有两组边对应相等，还有一组角对应相等，则两个三角形全等（ ）
2. 某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，
那么最省事的办法是（ ），这可以用三角形全等的哪种方法来解释
A.带①去 B.带②去 C.带③去 D.带①和②去
3. 三角形具有一个特有的性质：稳定性，它可以用三角形全等的哪种方法来解释
二、例题与变形
例1. 如图，点A、E、B、D在同一直线上，若△ABC≌△DEF，则以下成立的有（ ）
①AC∥DF； ②BC=EF； ③∠1=∠2； ④AE=BD （例1及其2个变形图形一样）
变形_1: 如图，已知AB=DE，∠1=∠2，AC∥DF，试说明BC=EF
变形_2:如图，已知AE=BD，AC∥DF，且AC=DF，试说明∠1=∠2
例2. 已知△AOB≌△COD，则你可以得到哪些等量等量关系
①∠A=∠C；②∠B=∠D；③AB=CD；④AO=CO；⑤BO=DO；⑥AD=CB
变形_1: 已知AB=CD，∠A=∠C，请说明AD=CB吗
变形_2: 已知△ABC≌△CDA，你能得到△AOB≌△COD吗 请说明理由.
变形_3: 已知∠1=∠2，，AO=CO，BO=DO，试说明△ABD≌△CDB
变形_4: 已知EB=ED，AB=CD，试说明∠B=∠D
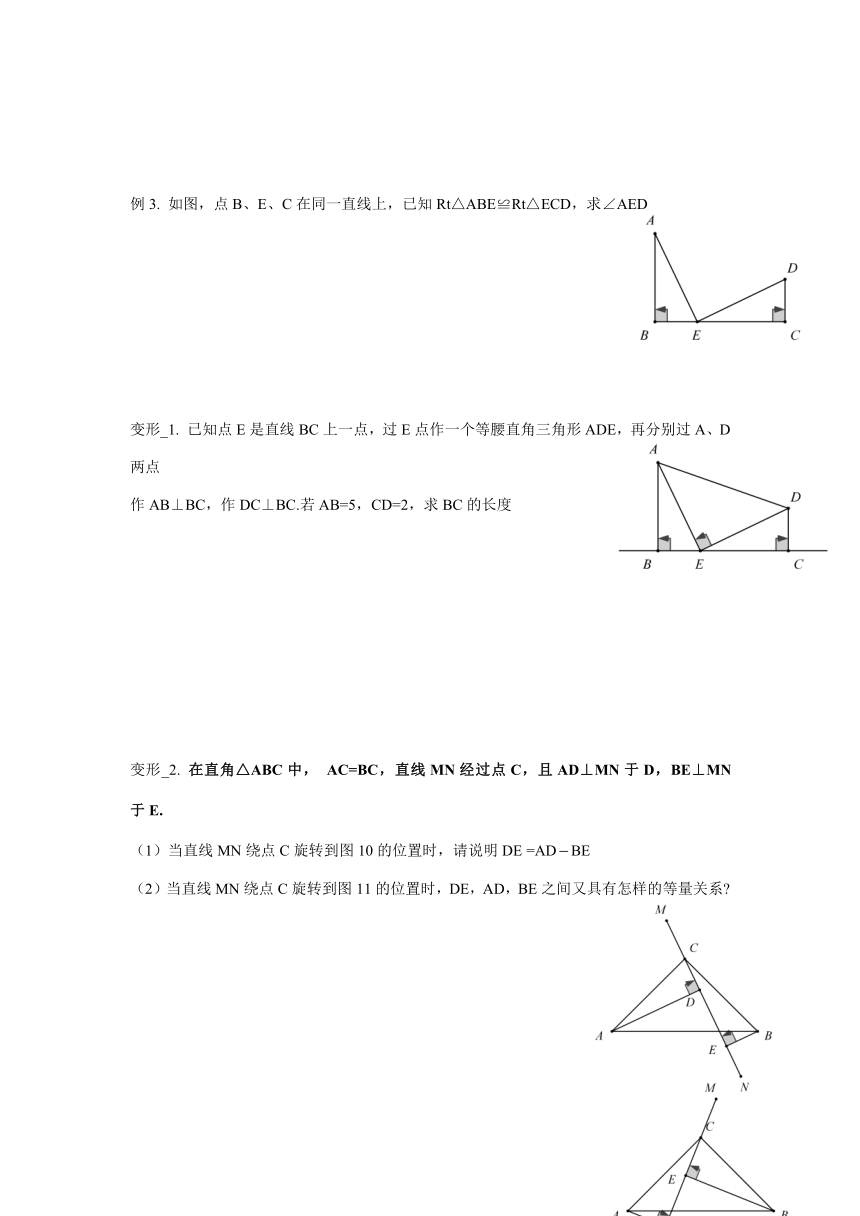
例3. 如图，点B、E、C在同一直线上，已知Rt△ABE≌Rt△ECD，求∠AED
变形_1. 已知点E是直线BC上一点，过E点作一个等腰直角三角形ADE，再分别过A、D两点
作AB⊥BC，作DC⊥BC.若AB=5，CD=2，求BC的长度
变形_2. 在直角△ABC中， AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.
（1）当直线MN绕点C旋转到图10的位置时，请说明DE =ADBE
（2）当直线MN绕点C旋转到图11的位置时，DE，AD，BE之间又具有怎样的等量关系
例4. △ABC是等边三角形，在三边上分别取点D、E、F，满足AD=BE=FC，
（1）试说明DE=EF；（2）求∠DEF的度数
变形_1: △ABC是等边三角形，在三边的延长线上分别取点D、E、F，满足BD=CE=AF，
试说明△DEF也是等边三角形【只需要说明 】
变形_2: △ABC是等边三角形，在三边上分别取点D、E、F，满足AD=BE=FC，如右图所示，分别连接AE，BF，CD. （1）试说明AE=BF=CD （2）试说明△GHI是等边三角形
例5. 把两个含有45°角的直角三角板（即△ABC与△CDE均为等腰直角三角形）如图放置（其中一组直角边重合），先连结BE，再连接AD并延长交BE于点F．
（1）找出图形中的全等三角形，并说明理由 （2）试说明AF⊥BE
备用图
变形_1: 以点A为顶点作三个等腰直角三角形（△ABC，△ADE），如图所示，连接BD，CE
（1）说明BD=CE （2）求∠BFC的度数
变形_2: ：以点A为顶点作三个等边三角形（△ABC，△ADE），连接CD，连接BE.
（1）请说明BD=CE （2）求∠BFC的度数
A
F
B
C
E
D