人教版2019必修一第三单元 函数的概念与性质单元测试(含解析)
文档属性
| 名称 | 人教版2019必修一第三单元 函数的概念与性质单元测试(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-03 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版2019必修一第三单元 函数的概念与性质
一、单选题
1.函数 的定义域是(??? )
A.??????????????????B.??????????????????C.??????????????????D.?
2.下列各组函数表示同一函数的是(??? )
A.????????????????????????????????B.?
C.???????????????????????????????????D.?
3.下列函数中,既是偶函数,又在 上单调递增的是(??? )
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
4.若幂函数 的图像经过点 ,则 的定义域为(??? )
A.?R??????????????????????????B.???????????????????????????C.???????????????????????????D.?
5.已知函数 ,则 (??? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
6.已知函数 是幂函数,且在 上是减函数,则实数m的值是( ???).
A.?-1或2?????????????????????????????????????????B.?2?????????????????????????????????????????C.?-1?????????????????????????????????????????D.?1
7.已知f(x)为R上的减函数,则满足f >f(1)的实数x的取值范围是(?? )
A.?(-∞,1)????????????????????????B.?(1,+∞)????????????????????????C.?(-∞,0)∪(0,1)????????????????????????D.?(-∞,0)∪(1,+∞)
8.已知函数 ,若 ,则 的取值范围是(??? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
二、多选题
9.下列函数中,满足f(2x)=2f(x)的是(??? )
A.?f(x)=|x|?????????????????????????????B.?f(x)=x-|x|?????????????????????????????C.?f(x)=x+1?????????????????????????????D.?f(x)=-x
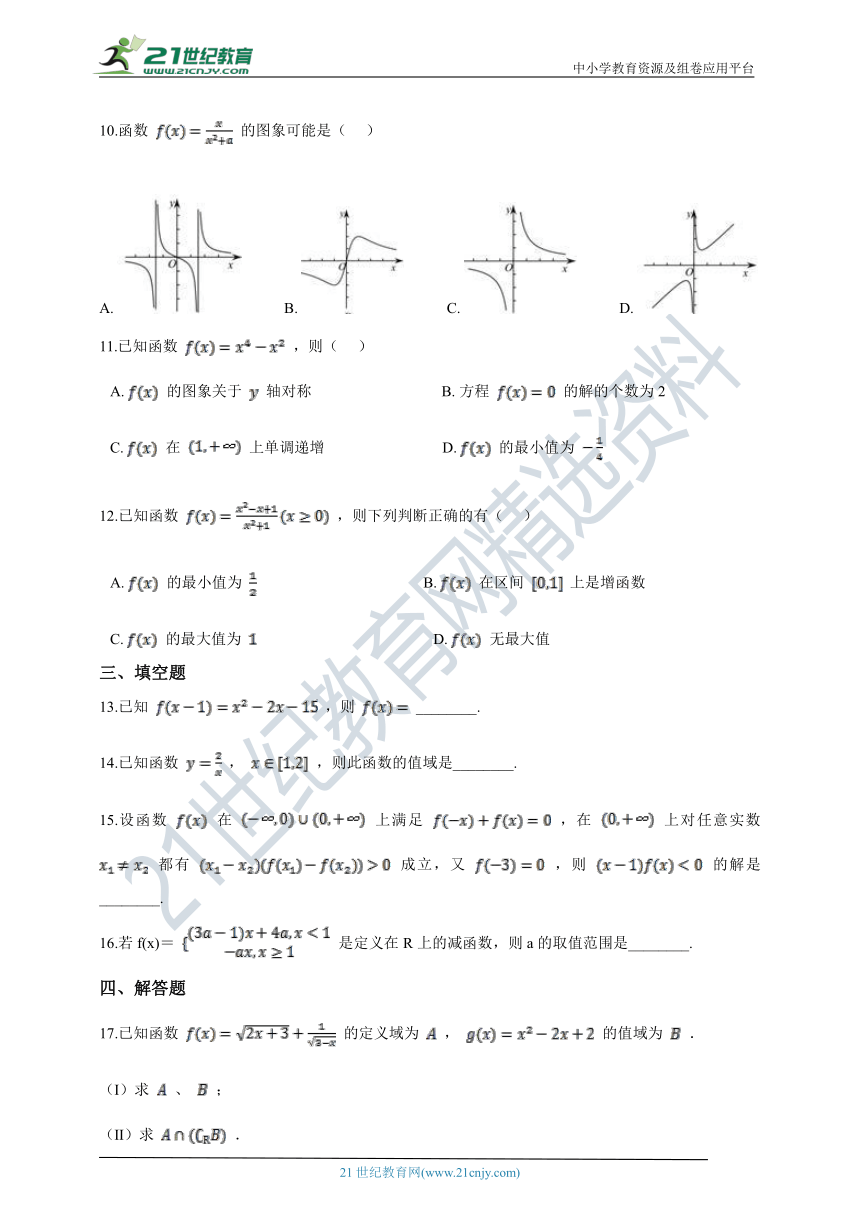
10.函数 的图象可能是(??? )
??????
A.????????????B.????????????C.????????????D.?
11.已知函数 ,则(??? )
A.? 的图象关于 轴对称??????????????????????????????????B.?方程 的解的个数为2
C.? 在 上单调递增???????????????????????????????D.? 的最小值为
12.已知函数 ,则下列判断正确的有(??? )
A.? 的最小值为 ????????????????????????????????????????????B.? 在区间 上是增函数
C.? 的最大值为 ??????????????????????????????????????????????D.? 无最大值
三、填空题
13.已知 ,则 ________.
14.已知函数 , ,则此函数的值域是________.
15.设函数 在 上满足 ,在 上对任意实数 都有 成立,又 ,则 的解是________.
16.若f(x)= 是定义在R上的减函数,则a的取值范围是________.
四、解答题
17.已知函数 的定义域为 , 的值域为 .
(Ⅰ)求 、 ;
(Ⅱ)求 .
18.若函数f(x)=2x+a是奇函数,
(1)求a的值;
(2)证明f(x)在R上是增函数。
19.已知函数 为定义在R上的偶函数,且当 时, .
(1)求 的解析式;
(2)在网格中绘制 的图像并求出函数 的值域.
20.已知幂函数 的图象经过点 .
(1)求 的解析式;
(2)若 ,求 的取值范围.
21.设函数 是定义在 上的奇函数,已知 ,且当 时, .
(Ⅰ)求 时,函数 的解析式;
(Ⅱ)判断函数 在 上的单调性,并用定义证明.
22.2020年初,新冠肺炎疫情袭击全国,对人民生命安全和生产生活造成严重影响.为降低疫情影响,某厂家拟尽快加大力度促进生产.已知该厂家生产某种产品的年固定成本为200万元,每生产 千件,需另投入成本为 ,当年产量不足80千件时, (万元).当年产量不小于 千件时, (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润 (万元)关于年产量 (千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?最大利润是多少?
答案解析部分
一、单选题
1.【答案】 B
【解】由题意可得 ,解得 或 ,
因此,函数 定义域为 。
故答案为:B.
2.【答案】 C
【解】对于A, , ,定义域不相同,故不是同一函数;
对于B, , ,定义域不相同,故不是同一函数;
对于C, , ,定义域和解析式都相同,是同一函数;
对于D,f(x)=x+1 , ,定义域不同,不是同一函数.
故答案为:C
3.【答案】 C
【解】对于A: 是奇函数,在 上单调递增,A不符合题意;
对于B: 是偶函数,在 上单调递减,B不符合题意符合题意;
对于C: ,其图象为:
图象关于 轴对称,是偶函数且在 上单调递增,C符合题意;
对于D: 定义域为 ,不关于原点对称,所以 既不是奇函数也不是偶函数, D不符合题意,
故答案为:C
4.【答案】 C
【解】 为幂函数, 设
又 的图像经过点 , ,解得: ,
的定义域为
故答案为:C
5.【答案】 A
【解】令 , , ,
则 ,
所以 。
故答案为:A。
6.【答案】 C
【解】 是幂函数, ,解得 或m=2,
当 时, 在 上是减函数,符合题意,
当 时, 在 上是增函数,不符合题意,
,
故答案为:C.
7.【答案】 D
【解】由题意,得 <1,当x<0时显然成立,当x>0时,x>1.
综上可得:实数x的取值范围是(-∞,0)∪(1,+∞)
故答案为:D.
8.【答案】 A
【解】由题意得: ,
当 时, ,不成立;
当 时, ,即 ,
解得 或 ,
所以 ,
当 时, ,即 ,无解,
综上所述: ,
所以 的取值范围是 。
故答案为:A。
二、多选题
9.【答案】 A,B,D
【解】在A中,f(2x)=|2x|=2|x|,2f(x)=2|x|,满足f(2x)=2f(x);
在B中,f(2x)=2x-|2x|=2(x-|x|)=2f(x),满足f(2x)=2f(x);
在C中,f(2x)=2x+1,2f(x)=2(x+1)=2x+2,不满足f(2x)=2f(x);
在D中,f(2x)=-2x=2(-x)=2f(x),满足f(2x)=2f(x)。
故答案为:ABD.
10.【答案】 A,B,C
解:A、当a<0时,函数的定义域为,当x>0时,在(0,),(,+∞)为增函数,则(0,),(,+∞)为减函数, 正确;
C、当a=0时, . 正确;?
BD、当a>0时, , 故D错误,当x>0时, ?, 当且仅当x=时取等号,则函数在(-∞,)上为减函数,在(,+∞)上为增函数?, 故选项B符合;
故答案为:ABC.
11.【答案】 A,C,D
【解】 定义域为 ,显然关于原点对称,又 ,所以 是偶函数,关于 轴对称,故答案为:项A符合题意.
令 即 ,解得: ,1, ,函数 有3个零点,故 错误;
令 , , 时,函数 , 都为递增函数,故 在 递增,故 正确;
由 时, 取得最小值 ,故 的最小值是 ,故 正确.
故答案为:ACD.
12.【答案】 A,C
【解】 ,
当 时, ,
当 时, ,
由于 在 , 上单调递减,
在 , 上单调递减,故 错误,
,
,当且仅当 时取等号,
,
,
综上所述 的值域为 , ,所以D错误,
故答案为:AC
三、填空题
13.【答案】
【解】令 ,则 ,
∴ ,∴ .
故答案为: .
14.【答案】 [1,2]
【解】因为函数 在区间 上为增函数,当 时, ,即 .
因此,函数 , 的值域为[1,2].
故答案为:[1,2].
15.【答案】
【解】由函数 定义域及 ,可知函数 为奇函数,
在 上对任意实数 都有 成立,
函数 在 上为增函数,
又函数 为奇函数, 函数 在 为增函数,
又 ,则 , 作出函数草图如图所示:
或 ,
根据 的图像可知 的解为: 。
故答案为: 。
16.【答案】
【解】由题意知, ,
解得 ,所以 .
故答案为:
四、解答题
17.【答案】 解:(Ⅰ)由 得
解得 .
,
所以 , .
(Ⅱ) ,所以
18.【答案】 (1)解:由题意得: ,
解得a=0;
(2)∵ ,
设-∞ ,
∴ f(x)在R上是增函数。
19.【答案】 (1)解:设 时, , ,则
的解析式为 .
(2)解:图像如图所示
由图可知值域为 .
20.【答案】 (1)解:设 .因为 的图象经过点 ,所以 ,解得 .
故
(2)解:由(1)可知 是定义域为 的增函数.
因为 ,所以 ,解得 .
故 的取值范围为
21.【答案】 解:(Ⅰ)由题可知, ,解得 ;
∴当 时, .
当 时, , .
∴ , .
(Ⅱ)∵ ,
∴函数 在 上为增函数.
证明:设 , 是 上任意实数,且 .
则 .
∵ , 且 ,
∴ , , .
∴ ,即: .
∴函数 在 上为增函数
22.【答案】 (1)解:因为每件商品售价为0.05万元,则 千件商品销售额为 万元,
依题意得:
当 时, ,
当 时, ,
所以
(2)解:当 时, ,
此时,当 时,即 万元.
当 时, ,
此时 ,即 万元,
由于 ,
所以当年产量为30千件时,该厂在这一商品生产中所获利润最大,最大利润为250万元.
_21?????????è?????(www.21cnjy.com)_
人教版2019必修一第三单元 函数的概念与性质
一、单选题
1.函数 的定义域是(??? )
A.??????????????????B.??????????????????C.??????????????????D.?
2.下列各组函数表示同一函数的是(??? )
A.????????????????????????????????B.?
C.???????????????????????????????????D.?
3.下列函数中,既是偶函数,又在 上单调递增的是(??? )
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
4.若幂函数 的图像经过点 ,则 的定义域为(??? )
A.?R??????????????????????????B.???????????????????????????C.???????????????????????????D.?
5.已知函数 ,则 (??? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
6.已知函数 是幂函数,且在 上是减函数,则实数m的值是( ???).
A.?-1或2?????????????????????????????????????????B.?2?????????????????????????????????????????C.?-1?????????????????????????????????????????D.?1
7.已知f(x)为R上的减函数,则满足f >f(1)的实数x的取值范围是(?? )
A.?(-∞,1)????????????????????????B.?(1,+∞)????????????????????????C.?(-∞,0)∪(0,1)????????????????????????D.?(-∞,0)∪(1,+∞)
8.已知函数 ,若 ,则 的取值范围是(??? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
二、多选题
9.下列函数中,满足f(2x)=2f(x)的是(??? )
A.?f(x)=|x|?????????????????????????????B.?f(x)=x-|x|?????????????????????????????C.?f(x)=x+1?????????????????????????????D.?f(x)=-x
10.函数 的图象可能是(??? )
??????
A.????????????B.????????????C.????????????D.?
11.已知函数 ,则(??? )
A.? 的图象关于 轴对称??????????????????????????????????B.?方程 的解的个数为2
C.? 在 上单调递增???????????????????????????????D.? 的最小值为
12.已知函数 ,则下列判断正确的有(??? )
A.? 的最小值为 ????????????????????????????????????????????B.? 在区间 上是增函数
C.? 的最大值为 ??????????????????????????????????????????????D.? 无最大值
三、填空题
13.已知 ,则 ________.
14.已知函数 , ,则此函数的值域是________.
15.设函数 在 上满足 ,在 上对任意实数 都有 成立,又 ,则 的解是________.
16.若f(x)= 是定义在R上的减函数,则a的取值范围是________.
四、解答题
17.已知函数 的定义域为 , 的值域为 .
(Ⅰ)求 、 ;
(Ⅱ)求 .
18.若函数f(x)=2x+a是奇函数,
(1)求a的值;
(2)证明f(x)在R上是增函数。
19.已知函数 为定义在R上的偶函数,且当 时, .
(1)求 的解析式;
(2)在网格中绘制 的图像并求出函数 的值域.
20.已知幂函数 的图象经过点 .
(1)求 的解析式;
(2)若 ,求 的取值范围.
21.设函数 是定义在 上的奇函数,已知 ,且当 时, .
(Ⅰ)求 时,函数 的解析式;
(Ⅱ)判断函数 在 上的单调性,并用定义证明.
22.2020年初,新冠肺炎疫情袭击全国,对人民生命安全和生产生活造成严重影响.为降低疫情影响,某厂家拟尽快加大力度促进生产.已知该厂家生产某种产品的年固定成本为200万元,每生产 千件,需另投入成本为 ,当年产量不足80千件时, (万元).当年产量不小于 千件时, (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润 (万元)关于年产量 (千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?最大利润是多少?
答案解析部分
一、单选题
1.【答案】 B
【解】由题意可得 ,解得 或 ,
因此,函数 定义域为 。
故答案为:B.
2.【答案】 C
【解】对于A, , ,定义域不相同,故不是同一函数;
对于B, , ,定义域不相同,故不是同一函数;
对于C, , ,定义域和解析式都相同,是同一函数;
对于D,f(x)=x+1 , ,定义域不同,不是同一函数.
故答案为:C
3.【答案】 C
【解】对于A: 是奇函数,在 上单调递增,A不符合题意;
对于B: 是偶函数,在 上单调递减,B不符合题意符合题意;
对于C: ,其图象为:
图象关于 轴对称,是偶函数且在 上单调递增,C符合题意;
对于D: 定义域为 ,不关于原点对称,所以 既不是奇函数也不是偶函数, D不符合题意,
故答案为:C
4.【答案】 C
【解】 为幂函数, 设
又 的图像经过点 , ,解得: ,
的定义域为
故答案为:C
5.【答案】 A
【解】令 , , ,
则 ,
所以 。
故答案为:A。
6.【答案】 C
【解】 是幂函数, ,解得 或m=2,
当 时, 在 上是减函数,符合题意,
当 时, 在 上是增函数,不符合题意,
,
故答案为:C.
7.【答案】 D
【解】由题意,得 <1,当x<0时显然成立,当x>0时,x>1.
综上可得:实数x的取值范围是(-∞,0)∪(1,+∞)
故答案为:D.
8.【答案】 A
【解】由题意得: ,
当 时, ,不成立;
当 时, ,即 ,
解得 或 ,
所以 ,
当 时, ,即 ,无解,
综上所述: ,
所以 的取值范围是 。
故答案为:A。
二、多选题
9.【答案】 A,B,D
【解】在A中,f(2x)=|2x|=2|x|,2f(x)=2|x|,满足f(2x)=2f(x);
在B中,f(2x)=2x-|2x|=2(x-|x|)=2f(x),满足f(2x)=2f(x);
在C中,f(2x)=2x+1,2f(x)=2(x+1)=2x+2,不满足f(2x)=2f(x);
在D中,f(2x)=-2x=2(-x)=2f(x),满足f(2x)=2f(x)。
故答案为:ABD.
10.【答案】 A,B,C
解:A、当a<0时,函数的定义域为,当x>0时,在(0,),(,+∞)为增函数,则(0,),(,+∞)为减函数, 正确;
C、当a=0时, . 正确;?
BD、当a>0时, , 故D错误,当x>0时, ?, 当且仅当x=时取等号,则函数在(-∞,)上为减函数,在(,+∞)上为增函数?, 故选项B符合;
故答案为:ABC.
11.【答案】 A,C,D
【解】 定义域为 ,显然关于原点对称,又 ,所以 是偶函数,关于 轴对称,故答案为:项A符合题意.
令 即 ,解得: ,1, ,函数 有3个零点,故 错误;
令 , , 时,函数 , 都为递增函数,故 在 递增,故 正确;
由 时, 取得最小值 ,故 的最小值是 ,故 正确.
故答案为:ACD.
12.【答案】 A,C
【解】 ,
当 时, ,
当 时, ,
由于 在 , 上单调递减,
在 , 上单调递减,故 错误,
,
,当且仅当 时取等号,
,
,
综上所述 的值域为 , ,所以D错误,
故答案为:AC
三、填空题
13.【答案】
【解】令 ,则 ,
∴ ,∴ .
故答案为: .
14.【答案】 [1,2]
【解】因为函数 在区间 上为增函数,当 时, ,即 .
因此,函数 , 的值域为[1,2].
故答案为:[1,2].
15.【答案】
【解】由函数 定义域及 ,可知函数 为奇函数,
在 上对任意实数 都有 成立,
函数 在 上为增函数,
又函数 为奇函数, 函数 在 为增函数,
又 ,则 , 作出函数草图如图所示:
或 ,
根据 的图像可知 的解为: 。
故答案为: 。
16.【答案】
【解】由题意知, ,
解得 ,所以 .
故答案为:
四、解答题
17.【答案】 解:(Ⅰ)由 得
解得 .
,
所以 , .
(Ⅱ) ,所以
18.【答案】 (1)解:由题意得: ,
解得a=0;
(2)∵ ,
设-∞
∴ f(x)在R上是增函数。
19.【答案】 (1)解:设 时, , ,则
的解析式为 .
(2)解:图像如图所示
由图可知值域为 .
20.【答案】 (1)解:设 .因为 的图象经过点 ,所以 ,解得 .
故
(2)解:由(1)可知 是定义域为 的增函数.
因为 ,所以 ,解得 .
故 的取值范围为
21.【答案】 解:(Ⅰ)由题可知, ,解得 ;
∴当 时, .
当 时, , .
∴ , .
(Ⅱ)∵ ,
∴函数 在 上为增函数.
证明:设 , 是 上任意实数,且 .
则 .
∵ , 且 ,
∴ , , .
∴ ,即: .
∴函数 在 上为增函数
22.【答案】 (1)解:因为每件商品售价为0.05万元,则 千件商品销售额为 万元,
依题意得:
当 时, ,
当 时, ,
所以
(2)解:当 时, ,
此时,当 时,即 万元.
当 时, ,
此时 ,即 万元,
由于 ,
所以当年产量为30千件时,该厂在这一商品生产中所获利润最大,最大利润为250万元.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
