10.4《探索三角形相似条件（1）》

(共13张PPT)
初中数学八年级下册
（苏科版）
10.4探索三角形相似的条件（1）
小明用白纸遮住了3个三角形的一部分，你能画出这3个三角形吗？
尝试：
A′
B′
A″
B″
A
B
（1）
（2）
（3）
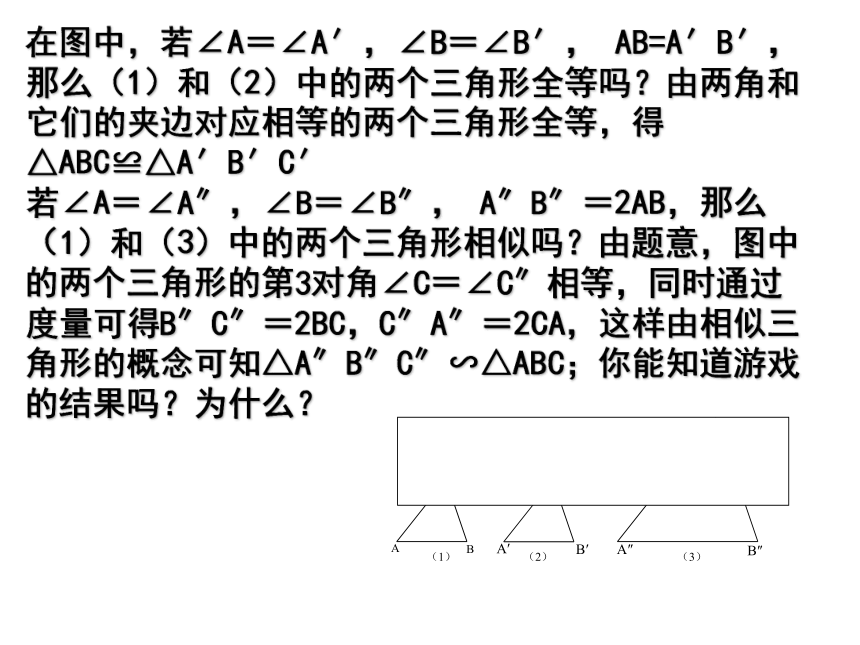
在图中，若∠A＝∠A′，∠B＝∠B′， AB=A′B′，那么（1）和（2）中的两个三角形全等吗？由两角和它们的夹边对应相等的两个三角形全等，得△ABC≌△A′B′C′
若∠A＝∠A″，∠B＝∠B″， A″B″＝2AB，那么（1）和（3）中的两个三角形相似吗？由题意，图中的两个三角形的第3对角∠C＝∠C″相等，同时通过度量可得B″C″＝2BC，C″A″＝2CA，这样由相似三角形的概念可知△A″B″C″∽△ABC；你能知道游戏的结果吗？为什么？
A′
B′
A″
B″
A
B
（1）
（2）
（3）
由此得判定方法一：如果一个三角形的
两个角与另一个三角形的两个角对应相
等，那么这两个三角形相似。　
几何语言：在△ABC与△A″B″C″中，
∵∠A＝∠A″，∠B＝∠B″，
∴△A″B″C″∽△ABC
试一试：
关于三角形相似下列叙述不正确的是 ( 　)
A、有一个底角对应相等的两个等腰三角形相似;
B、有一个角对应相等的两个等腰三角形相似;
C、所有等边三角形都相似;
D、顶角对应相等的两个等腰三角形相似.
试一试：
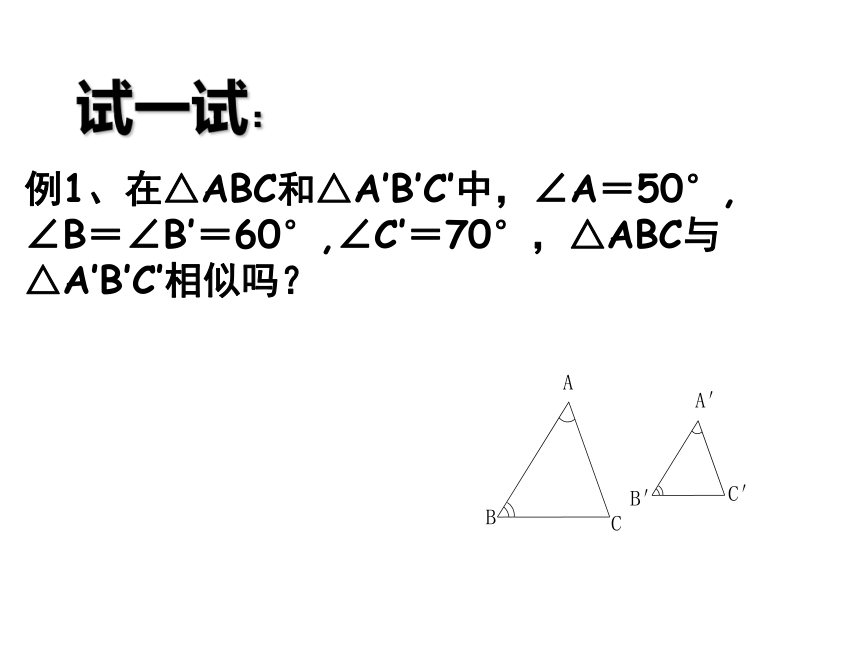
例1、在△ABC和△A′B′C′中，∠A＝50°,
∠B＝∠B′＝60°,∠C′＝70°，△ABC与
△A′B′C′相似吗？
A
B
C
A′
B′
C′
试一试：
例2、如图，在方格图中，画△A′B′C′，
使A′C′∥AC，B′C′∥BC,
(1)如果∠A＝25 ,∠B＝135 ，
那么∠A′＝ ，∠B′＝ ，
∠C′＝ ；
(2) 测量两个三角形的三边长后
判定△ABC与A′B′C′是否相似？
(3)发现：两角 的两三角形相似
B
B′
C′
A′
C
A
尝试：
如图，DE∥BC，分别交AB、AC于点D、E，
△ADE与△ABC相似吗？为什么？
【变题】如图，点A、B、D与点A、C、E
分别在一条直线上，如果DE∥BC，△ADE
与△ABC相似吗？为什么？
A
D
E
B
C
E
D
A
B
C
A
B
C
E
D
由此得：平行于三角形一边的直线与
其他两边（或两边的延长线）相交，
所构成的三角形与原三角形相似.
几何语言：∵DE∥BC ∴△ADE∽△ABC
尝试：
C
B
D
A
如图，Rt△ABC中，CD是斜边AB上的高,
（1）试说明△ABC∽△CBD∽△ACD.
（2）根据△ABC∽△ACD有
∴AC2＝AD·AB, 类似地,你还可以
得到哪些结论？
发散探究
过△ABC的边AB上一点D作一条直线与另一边ＡＣ相交，截得的小三角形与△ABC相似，这样的直线有几条？请把它们一一作出来。
这样的直线有几条？
C
D ●
Ａ
Ｂ
B
C
A
D
E
E
B
C
A
D
∴△ ADE∽ △ABC
∴△ AED∽ △ABC
∠AED=∠C(或DE∥BC)
∠AＥＤ=∠Ｂ
作DE,使
作DE,使
又∠ Ａ＝∠Ａ
又∠ Ａ＝∠Ａ
归纳总结
1、探索三角形相似的条件（1），并运用这一条件解决有关问题
2、经历“操作——观察——探索——说理”的数学活动过程，发展合情推理和有条理的表达能力.