苏科版七年级下学期期中复习讲义

(共33张PPT)
苏科版七下期中复习建议
期中复习教学中几个值得关注的问题
1.本学期以来的教学内容有哪些？
数与代数： 幂的运算、整式的乘法、因式分解
图形与几何：
1、图形的性质：平行线的性质与判定、三角形
2、图形的变化：图形的平移
综合与实践：
设计平移图案、比较生活中的较大数和较小数、拼图
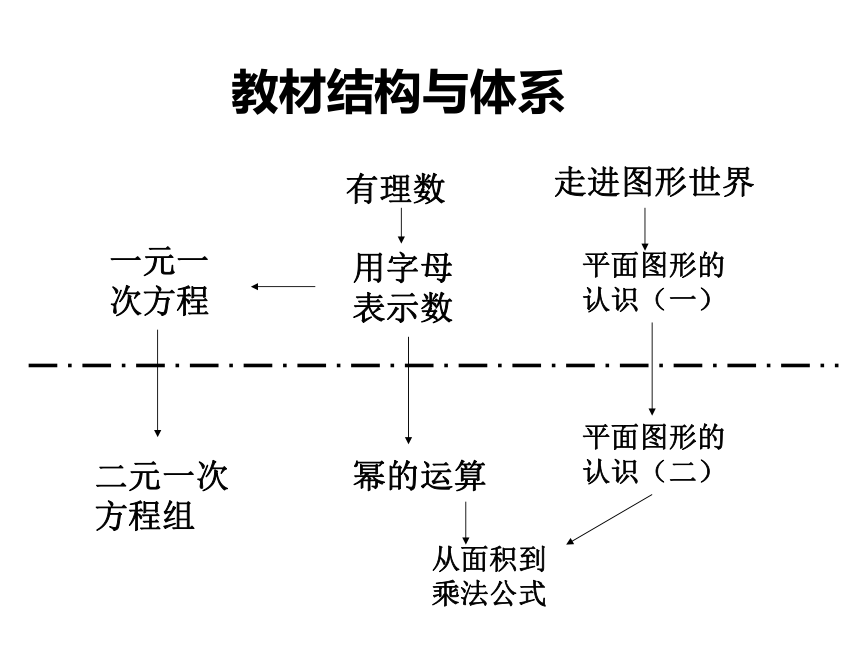
教材结构与体系
有理数
一元一次方程
用字母表示数
走进图形世界
平面图形的认识（一）
二元一次方程组
幂的运算
平面图形的认识（二）
从面积到乘法公式
整式
（1）了解整数指数幂的意义和基本性质，会用科学记数法表示数（包括在计算器上表示）.
（2）了解整式的概念，掌握合并同类项和去括号的法则，能进行简单的整式加法和减法运算；能进行简单的整式乘法运算（其中多项式相乘仅指一次式之间以及一次式与二次式相乘 ）.
（3）能推导乘法公式：(a + b)(a - b) = a 2- b 2；
(a + b)2 = a 2 + 2ab + b 2, 了解公式的几何背景，并能利用公式进行简单计算.
（4）能用提公因式法、公式法（直接利用公式不超过二次）进行因式分解（系数是正整数）.

课标要求
一、数与代数
1.相交线与平行线
（1）掌握基本事实：过一点有且只有一条直线与这条直线垂直.
（2）识别同位角、内错角、同旁内角.
（3）理解平行线概念；掌握基本事实：两条直线被第三条直线所截，如果同位角相等，那么两直线平行.
（4）掌握基本事实：过直线外一点有且只有一条直线与这条直线平行.
（5）掌握平行线的性质定理：两条平行直线被第三条直线所截，同位角相等.
（6）能用三角尺和直尺过已知直线外一点画这条直线的平行线.
（7）探索平行线的判定定理：两条直线被第三条直线所截，如果内错角相等（或同旁内角互补），那么两直线平行；探索平行线的性质定理：两条平行直线被第三条直线所截，内错角相等（或同旁内角互补）.
（8）了解平行于同一条直线的两条直线平行.
二、图形的性质
2.三角形
（1）理解三角形及其内角、外角、中线、高线、角平分线等概念，会按照角的大小对三角形进行分类，了解三角形的稳定性.
（2）探索三角形的内角和定理.掌握它的推论：三角形的外角等于与它不相邻的两个内角的和.
（3）理解三角形的任意两边之和大于第三边.
二、图形的性质
3.四边形、多边形
探索并掌握多边形内角和与外角和公式。
三、图形的变化
图形的平移
（1）通过具体实例认识平移，探索它的基本性质：一个图形和它经过平移所得的图形中，两组对应点的连线平行且相等.
（2）认识和欣赏平移在自然界和现实生活中的应用.
（3）运用图形的轴对称、旋转、平移进行图案设计.
2.注重课本中基本知识的内在联系，让学生形成整体知识网络.
第九章
《从面积到乘法公式》
课标要求：
数学知识的教学，应注重学生对所学知识的理解，体会数学知识之间的关联.
学生掌握数学知识，不能依赖死记硬背，而应以理解为基础，并在知识的应用中不断巩固和深化.
幂的运算
平面图形的认识（二）
从面积到乘法公式
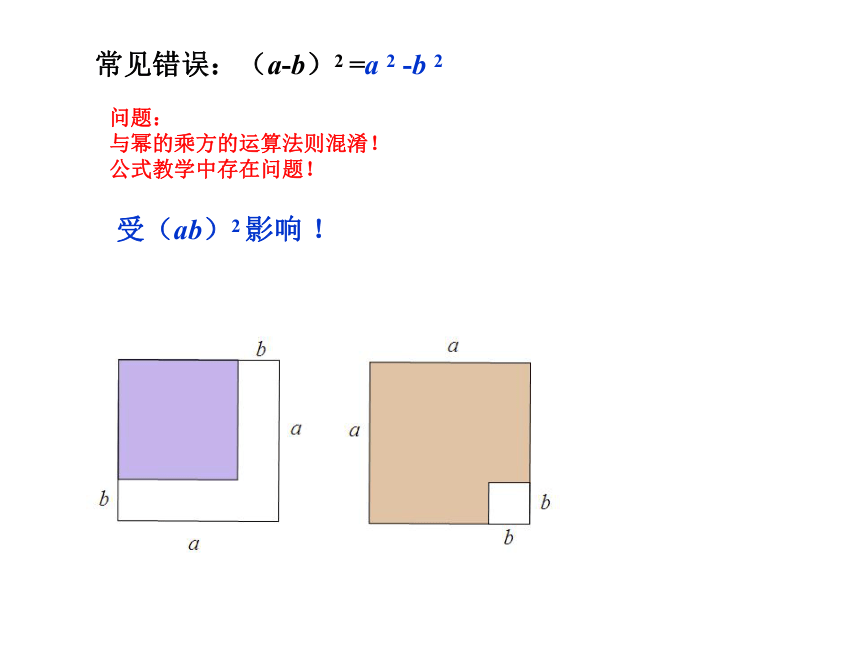
常见错误：（a-b）2 =a 2 -b 2
问题：
与幂的乘方的运算法则混淆！
公式教学中存在问题！
受（ab）2 影响 ！
3.有效的矫正练习，提高学生的运算能力.
例：（-a-b）2 = -(a+b) 2
问题：
算理不明！
学生只有理解了计算的道理，才能“创造”出计算的方法，才能理解和掌握计算方法，才能正确迅速地计算.
本题应分两步进行计算
第一步：提负号
第二步：运用（ab）n = （ab）n
正解：（-a-b）2 = [-(a+b) ]2 = (a+b)2
知其所以然，最终让你的学生
通过观察比较，归纳方法、结果，简化算法
符号化归
（-a 2 ）3 （-a 3 ）2
易错符号问题
（-x-y）(-x+y)
（-1）4
(x+2) (x-3) -（x+1）2
例：课本P.69
常见问题：老师评讲过，下次还错！
不如进行一次类比教学：
（2a-b+3）(2a-b-3) （2a-b+3）(2a+b+3)
（2a-b+3）(-2a-b+3) （2a-b+3）(2a+b-3)
（2a-b+3）(-2a-b-3) （2a-b+3）(-2a+b+3)
（2a-b+3）(-2a+b-3)
南京市中考数学命题以《全日制义务教育数学课程标准》（实验稿）为依据，全卷以初中学段的知识与技能为基准，突出对学生基本的数学素养的评价，恰当评价学生的基础知识和基本技能．特别关注教材中最基础和最核心的内容，即所有学生在学习数学和运用数学解决问题过程中最为重要的，必须掌握的核心观念、思想方法、基本概念和常用技能．
4.通过三章的学习，我们的学生积累了哪些解决问题的数学经验？
整体思想、转化、分类讨论、数形结合思想方法的应用
整体思想:
从问题的整体观点出发，通过研究问题的整体形式、整体结构、整体特征，从而对问题进行整体处理的解题思想方法，称为整体思想.
整体换元
整体代入
整体思想
课本P67
课本P80
本质：整体换元
a2+b2+2ab=7 a2+b2-2ab =3
转化思想： 转化也称化归，它是指将未知的，陌生的，复杂的问题通过演绎归纳转化为已知的，熟悉的，简单的问题，从而使问题顺利解决的数学思想.
常常把有待解决或难以解决的问题，通过某种转化手段，使它转化成已经解决或比较容易解决的问题，从而求得原问题的解答，这里运用的就是转化思想.
掌握转化思想有利于我们从更深的层次去揭示、把握数学知识、方法之间的内在联系，树立辩证的观点，提高分析问题和解决问题的能力.
(-a+b)(a–b)
化归
(a+b)2
(a-b)2
（-a+b）2 (-a–b) 2
(-a+b) (a–b)
(-a+b) (b–a)
课本P27--28
转化点：
多边形问题转化为三角形问题
转化点：
1.多乘多转化成单乘多
2.单乘多再转化为单乘单
课本61
分类讨论思想
分类讨论是比较数学对象本质属性的相同点和差异点，根据数量关系或空间形式的某一标准将数学对象分为不同种类，然后分别对它们进行讨论，得出各种情况下相应结论的数学思想方法.
分类是解决数学问题的手段和策略之一，通过分类可以化整为零，化一般为特殊，变抽象为具体，可以把一个复杂问题分解成若干个相对简单明了的问题.
有些数学概念是分类给出的，如：上学期绝对值的概念是分类给出的,
例：∣a∣=1，则a=_____.
有些数学问题（尤为几何题）依条件画出的图形的位置或形状不能确定，就要运用分类讨论的思想进行解答 ，如：遇到三角形高的问题
有些数学问题的数学表达式，它的已知量不是以确定的常数给出的,
例 x2+kx+4=(x+a)2 ，则a=____.
有些数学问题的条件或结论不唯一确定，它们有几种可能，这时，也需要进行分类讨论 ,如：
例：如图，它是由6个面积为1的小正方形组成的长方形，点A，B，C，D，E，F是小正方形的顶点，以这六个点中的任意三点为顶点，可以组成_____个面积是1的三角形．
10
数形结合思想：
所谓数形结合就是根据数学问题的条件和结论之间的内在联系，既分析其代数含义，又揭示其几何意义，使数量关系和几何形式巧妙、和谐的结合起来，并充分利用这种“结合”，寻求解题思路，使问题得以解决.
如图，有A、B、C三种不同型号的卡片，每种卡片各有10 张.其中A型卡片是边长为a的正方形，B型卡片是长为b、宽为a的长方形，C型卡片是边长为b的正方形．其中A型卡片是边长为a的正方形，B型卡片是长为b、宽为a的长方形，C型卡片是边长为b的正方形.
（1）从其中取出若干张卡片，每种卡片至少取一张，把取出的这些卡片拼成一个正方形（所拼的图中既不能有缝隙，也不能有重合部分），能拼成几种不同的正方形，并说说你这样拼的理由；
（2）从其中取出17张卡片，每种卡片至少取出一张，取出的这些卡片能否拼成一个正方形（所拼的图中既不能有缝隙，也不能有重合部分），说说你的理由.
问题(1)要求能拼成几种不同的正方形，并要说明拼图的理由，对于学生来说直接回答难度较大，我们可以设置一下问题，帮助学生来分析问题.
问1：利用这三种卡片能拼成边长为(a+b)的正方形吗？
问2：能拼成边长为(2a+b)的正方形吗？
问3：边长为(2a+3b)呢？
通过这三个问题的设置，学生可以通过拼图的方法来验证是否可行，在验证的过程中学生易发现：
边长为(a+b)时，拼成的正方形面积为(a+b)2=a2+2ab+b2，此时需要1张A卡片，2张B卡片，1张C卡片；
同理，边长为(2a+b)时，拼成的正方形面积为(2a+b)2=4a2+4ab+b2，此时需要4张A卡片，4张B卡片，1张C卡片；
而边长为(2a+3b)时，拼成的正方形面积为(2a+3b)2=4a2+12ab+9b2，此时需要4张A卡片，12张B卡片，9张C卡片，显然不符合题意.
从而发现问题(1)可以从拼图问题转化为完全平方公式的运用，实现从图形面积到整式乘法运算的数形结合.
形 数
本题是数形结合思想的典型应用，是从形到数的转化，对几何图形的整体分析，对完全平方公式的灵活应用变形整理是解决此题的关键．
有了问题(1)的经验，我们将拼图问题转化为完全平方公式的运用，那么对于问题(2)，是否能从其中取出17张卡片拼成正方形，实际上就转化为：
假设存在这样的正方形，不妨设这个正方形的边长为(xa+yb)，则这个正方形的面积为(xa+yb)2=x2a2+2xyab+y2b2，即此时需要x2张A卡片，2xy张B卡片，y2张C卡片，因此总共需要(x2+2xy+y2)张卡片，即(x+y)2张卡片.那么根据题意，(x+y)2=17，因此不存在这样的x、y满足题意，因此不能从其中取出17张卡片拼成正方形.
数形结合思想：课本P64
数形结合思想：课本P66
数形结合思想：课本P68
数形结合思想：课本P68
数形结合思想：课本P77
数形结合思想：课本P78
小结与思考
数形结合思想：课本P81
谢谢！