第13章 全等三角形 13.2.3边角边 练习题 2021-2022学年八年级数学华东师大版上册(word版含答案)
文档属性
| 名称 | 第13章 全等三角形 13.2.3边角边 练习题 2021-2022学年八年级数学华东师大版上册(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 148.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-03 11:24:06 | ||
图片预览



文档简介
13.2.3 边角边
【基础练习】
知识点
1 基本事实“S.A.S.”及其运用
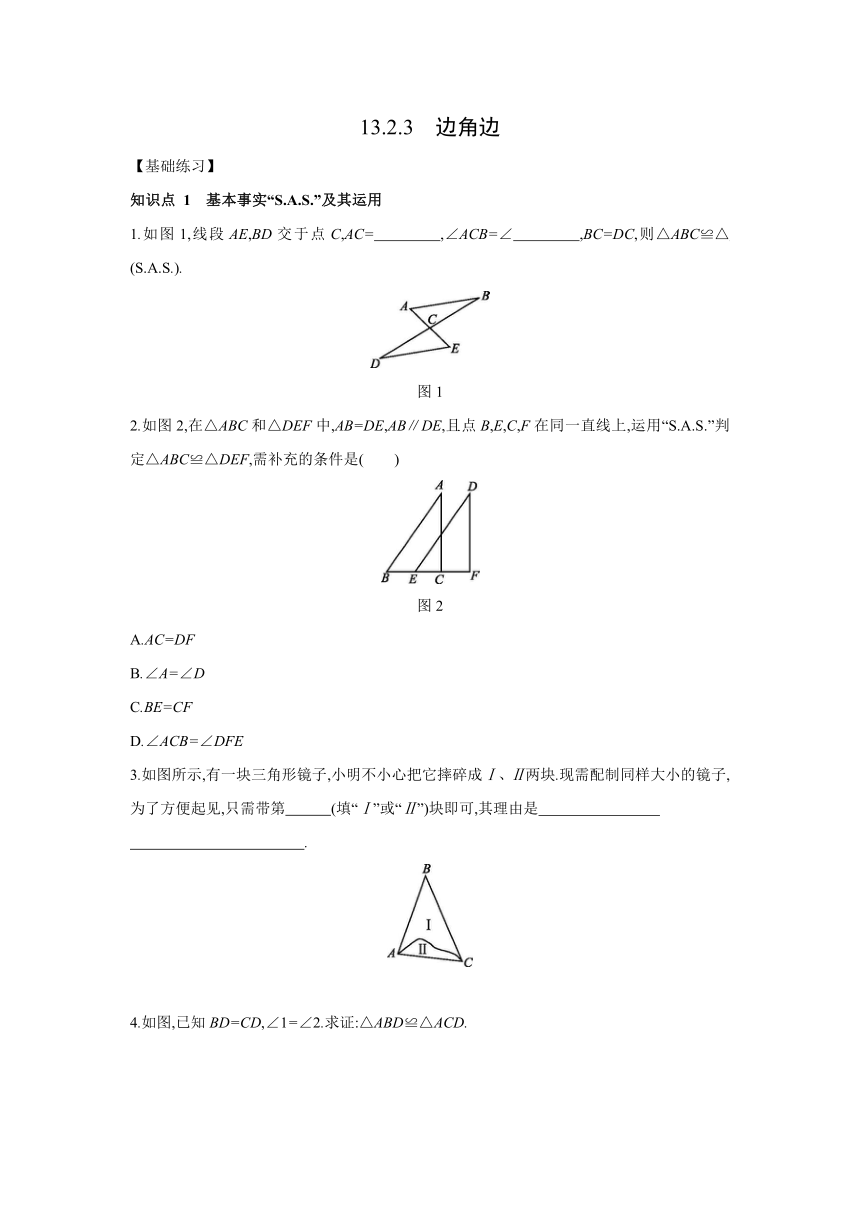
1.如图1,线段AE,BD交于点C,AC= ,∠ACB=∠ ,BC=DC,则△ABC≌△ (S.A.S.).?
图1
2.如图2,在△ABC和△DEF中,AB=DE,AB∥DE,且点B,E,C,F在同一直线上,运用“S.A.S.”判定△ABC≌△DEF,需补充的条件是( )
图2
A.AC=DF
B.∠A=∠D
C.BE=CF
D.∠ACB=∠DFE
3.如图所示,有一块三角形镜子,小明不小心把它摔碎成Ⅰ、Ⅱ两块.现需配制同样大小的镜子,为了方便起见,只需带第 (填“Ⅰ”或“Ⅱ”)块即可,其理由是
.?
4.如图,已知BD=CD,∠1=∠2.求证:△ABD≌△ACD.
5.已知:如图∠BAC=∠DAM,点N在AC上,且AN=AB,AD=AM.
求证:∠B=∠ANM.
知识点
2 “边边角”不能判定三角形全等
6.下面各组条件中,能使△ABC≌△DEF的是( )
A.AB=DE,∠A=∠D,BC=EF
B.AB=BC,∠B=∠E,DE=EF
C.AB=EF,∠A=∠D,AC=DF
D.BC=EF,∠C=∠F,AC=DF
7.下面是胡老师带领学生探究“S.S.A.”能否判定两个三角形全等的过程,请填空:
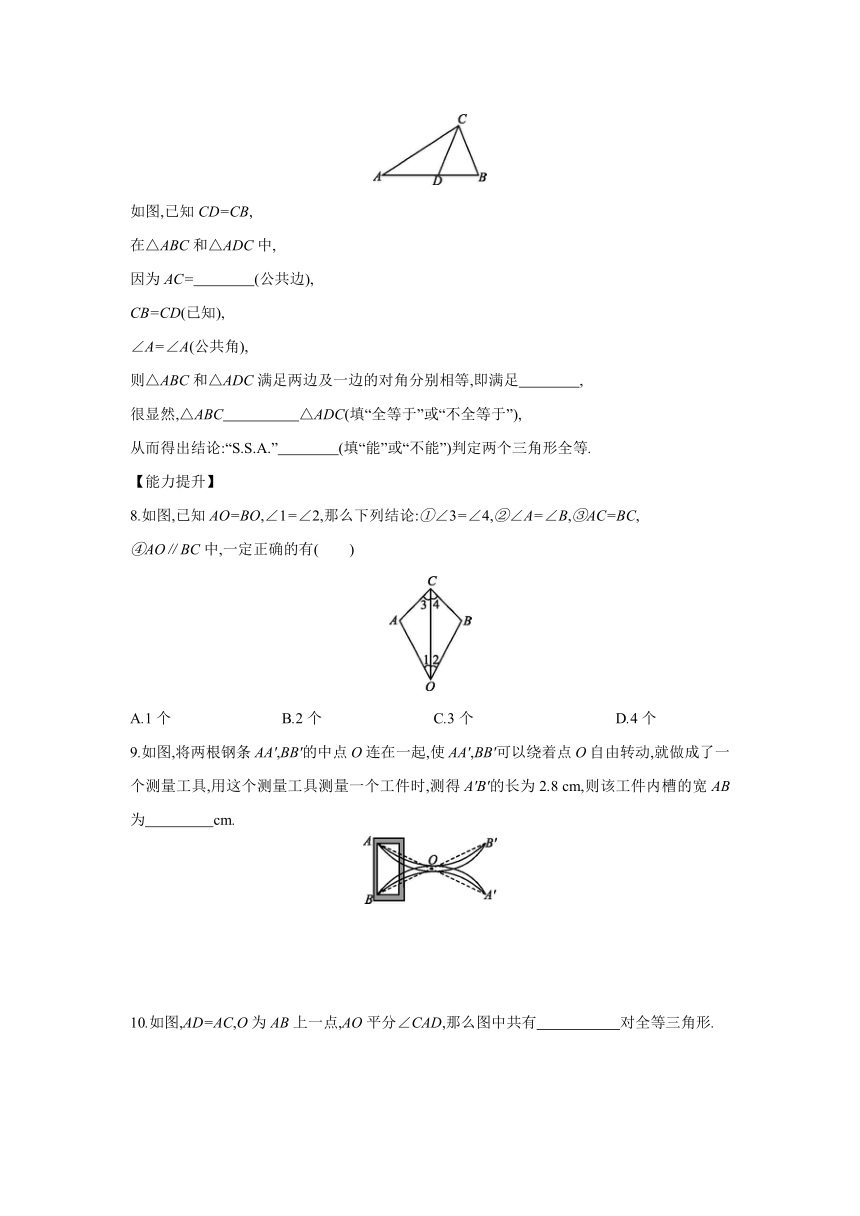
如图,已知CD=CB,
在△ABC和△ADC中,
因为AC= (公共边),?
CB=CD(已知),
∠A=∠A(公共角),
则△ABC和△ADC满足两边及一边的对角分别相等,即满足 ,?
很显然,△ABC △ADC(填“全等于”或“不全等于”),?
从而得出结论:“S.S.A.” (填“能”或“不能”)判定两个三角形全等.?
【能力提升】
8.如图,已知AO=BO,∠1=∠2,那么下列结论:①∠3=∠4,②∠A=∠B,③AC=BC,
④AO∥BC中,一定正确的有( )
A.1个
B.2个
C.3个
D.4个
9.如图,将两根钢条AA',BB'的中点O连在一起,使AA',BB'可以绕着点O自由转动,就做成了一个测量工具,用这个测量工具测量一个工件时,测得A'B'的长为2.8
cm,则该工件内槽的宽AB为
cm.?
10.如图,AD=AC,O为AB上一点,AO平分∠CAD,那么图中共有
对全等三角形.?
11.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠AFB=∠DEC.
12.如图,点B,F,C,E在同一直线上,AB=DE,BF=CE,AB∥DE.求证:AC=DF.
13.如图所示,已知AC=AD,AE平分∠CAD,在射线AE上任取除点A以外的一点F,连结FC,FD,所构成的两个三角形全等吗?若点F是在AE的反向延长线上取得的点呢?
14.学习了“全等三角形”的知识后,老师布置了一道作业题:如图①,已知在△ABC中,AB=AC,P是△ABC内任意一点,连结AP,将AP绕点A顺时针旋转至AQ处,使∠QAP=∠BAC,连结BQ,CP.求证:BQ=CP.
小亮是个爱动脑筋的学生,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP.之后,他将点P移到等腰三角形ABC外,原题中其他条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
答案
1.EC ECD EDC
2.C [解析]
补充BE=CF,理由如下:
∵AB∥DE,
∴∠ABC=∠DEF.
∵BE=CF,
∴BC=EF.
在△ABC和△DEF中,
∵AB=DE,∠ABC=∠DEF,BC=EF,
∴△ABC≌△DEF(S.A.S.).
故选C.
3.Ⅰ 根据“S.A.S.”确定三角形全等
4.证明:在△ABD与△ACD中,
∵BD=CD,∠1=∠2,AD=AD,
∴△ABD≌△ACD(S.A.S.).
5.证明:∵∠BAC=∠DAM,∠BAC=∠BAD+∠DAC,∠DAM=∠DAC+∠NAM,
∴∠BAD=∠NAM.
在△BAD和△NAM中,
∵AB=AN,∠BAD=∠NAM,AD=AM,
∴△BAD≌△NAM(S.A.S.),
∴∠B=∠ANM.
6.D 7.AC S.S.A. 不全等于 不能
8.C [解析]
在△AOC与△BOC中,因为AO=BO,∠1=∠2,OC=OC,所以△AOC≌△BOC,由此可得到①∠3=∠4,②∠A=∠B,③AC=BC.故选C.
9.2.8
10.3 [解析]
△AOC≌△AOD,△ABC≌△ABD,△BOC≌△BOD.
11.证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE.
在△ABF和△DCE中,
∵AB=DC,∠B=∠C,BF=CE,
∴△ABF≌△DCE(S.A.S.),
∴∠AFB=∠DEC.
12.证明:∵AB∥DE,
∴∠B=∠E.
∵BF=CE,
∴BF+FC=CE+FC,即BC=EF.
在△ABC和△DEF中,
∵AB=DE,∠B=∠E,BC=EF,
∴△ABC≌△DEF(S.A.S.),
∴AC=DF.
13.解:全等.在△ACF和△ADF中,因为AC=AD(已知),∠CAE=∠DAE(角平分线的定义),AF=AF(公共边),所以△ACF≌△ADF(S.A.S.).
若点F是在AE的反向延长线上取得的点,两三角形仍然全等.
因为点F在AE的反向延长线上,
所以∠CAF=180°-∠CAE,∠DAF=180°-∠DAE,而∠CAE=∠DAE,
所以∠CAF=∠DAF.
在△ACF和△ADF中,
因为AC=AD,∠CAF=∠DAF,AF=AF,
所以△ACF≌△ADF(S.A.S.).
14.证明:由旋转的性质可知AQ=AP.
∵∠QAP=∠BAC,
∴∠QAP+∠PAB=∠PAB+∠BAC,
即∠QAB=∠PAC.
在△ABQ和△ACP中,
∵AQ=AP,∠QAB=∠PAC,AB=AC,
∴△ABQ≌△ACP,∴BQ=CP.
【基础练习】
知识点
1 基本事实“S.A.S.”及其运用
1.如图1,线段AE,BD交于点C,AC= ,∠ACB=∠ ,BC=DC,则△ABC≌△ (S.A.S.).?
图1
2.如图2,在△ABC和△DEF中,AB=DE,AB∥DE,且点B,E,C,F在同一直线上,运用“S.A.S.”判定△ABC≌△DEF,需补充的条件是( )
图2
A.AC=DF
B.∠A=∠D
C.BE=CF
D.∠ACB=∠DFE
3.如图所示,有一块三角形镜子,小明不小心把它摔碎成Ⅰ、Ⅱ两块.现需配制同样大小的镜子,为了方便起见,只需带第 (填“Ⅰ”或“Ⅱ”)块即可,其理由是
.?
4.如图,已知BD=CD,∠1=∠2.求证:△ABD≌△ACD.
5.已知:如图∠BAC=∠DAM,点N在AC上,且AN=AB,AD=AM.
求证:∠B=∠ANM.
知识点
2 “边边角”不能判定三角形全等
6.下面各组条件中,能使△ABC≌△DEF的是( )
A.AB=DE,∠A=∠D,BC=EF
B.AB=BC,∠B=∠E,DE=EF
C.AB=EF,∠A=∠D,AC=DF
D.BC=EF,∠C=∠F,AC=DF
7.下面是胡老师带领学生探究“S.S.A.”能否判定两个三角形全等的过程,请填空:
如图,已知CD=CB,
在△ABC和△ADC中,
因为AC= (公共边),?
CB=CD(已知),
∠A=∠A(公共角),
则△ABC和△ADC满足两边及一边的对角分别相等,即满足 ,?
很显然,△ABC △ADC(填“全等于”或“不全等于”),?
从而得出结论:“S.S.A.” (填“能”或“不能”)判定两个三角形全等.?
【能力提升】
8.如图,已知AO=BO,∠1=∠2,那么下列结论:①∠3=∠4,②∠A=∠B,③AC=BC,
④AO∥BC中,一定正确的有( )
A.1个
B.2个
C.3个
D.4个
9.如图,将两根钢条AA',BB'的中点O连在一起,使AA',BB'可以绕着点O自由转动,就做成了一个测量工具,用这个测量工具测量一个工件时,测得A'B'的长为2.8
cm,则该工件内槽的宽AB为
cm.?
10.如图,AD=AC,O为AB上一点,AO平分∠CAD,那么图中共有
对全等三角形.?
11.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠AFB=∠DEC.
12.如图,点B,F,C,E在同一直线上,AB=DE,BF=CE,AB∥DE.求证:AC=DF.
13.如图所示,已知AC=AD,AE平分∠CAD,在射线AE上任取除点A以外的一点F,连结FC,FD,所构成的两个三角形全等吗?若点F是在AE的反向延长线上取得的点呢?
14.学习了“全等三角形”的知识后,老师布置了一道作业题:如图①,已知在△ABC中,AB=AC,P是△ABC内任意一点,连结AP,将AP绕点A顺时针旋转至AQ处,使∠QAP=∠BAC,连结BQ,CP.求证:BQ=CP.
小亮是个爱动脑筋的学生,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP.之后,他将点P移到等腰三角形ABC外,原题中其他条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
答案
1.EC ECD EDC
2.C [解析]
补充BE=CF,理由如下:
∵AB∥DE,
∴∠ABC=∠DEF.
∵BE=CF,
∴BC=EF.
在△ABC和△DEF中,
∵AB=DE,∠ABC=∠DEF,BC=EF,
∴△ABC≌△DEF(S.A.S.).
故选C.
3.Ⅰ 根据“S.A.S.”确定三角形全等
4.证明:在△ABD与△ACD中,
∵BD=CD,∠1=∠2,AD=AD,
∴△ABD≌△ACD(S.A.S.).
5.证明:∵∠BAC=∠DAM,∠BAC=∠BAD+∠DAC,∠DAM=∠DAC+∠NAM,
∴∠BAD=∠NAM.
在△BAD和△NAM中,
∵AB=AN,∠BAD=∠NAM,AD=AM,
∴△BAD≌△NAM(S.A.S.),
∴∠B=∠ANM.
6.D 7.AC S.S.A. 不全等于 不能
8.C [解析]
在△AOC与△BOC中,因为AO=BO,∠1=∠2,OC=OC,所以△AOC≌△BOC,由此可得到①∠3=∠4,②∠A=∠B,③AC=BC.故选C.
9.2.8
10.3 [解析]
△AOC≌△AOD,△ABC≌△ABD,△BOC≌△BOD.
11.证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE.
在△ABF和△DCE中,
∵AB=DC,∠B=∠C,BF=CE,
∴△ABF≌△DCE(S.A.S.),
∴∠AFB=∠DEC.
12.证明:∵AB∥DE,
∴∠B=∠E.
∵BF=CE,
∴BF+FC=CE+FC,即BC=EF.
在△ABC和△DEF中,
∵AB=DE,∠B=∠E,BC=EF,
∴△ABC≌△DEF(S.A.S.),
∴AC=DF.
13.解:全等.在△ACF和△ADF中,因为AC=AD(已知),∠CAE=∠DAE(角平分线的定义),AF=AF(公共边),所以△ACF≌△ADF(S.A.S.).
若点F是在AE的反向延长线上取得的点,两三角形仍然全等.
因为点F在AE的反向延长线上,
所以∠CAF=180°-∠CAE,∠DAF=180°-∠DAE,而∠CAE=∠DAE,
所以∠CAF=∠DAF.
在△ACF和△ADF中,
因为AC=AD,∠CAF=∠DAF,AF=AF,
所以△ACF≌△ADF(S.A.S.).
14.证明:由旋转的性质可知AQ=AP.
∵∠QAP=∠BAC,
∴∠QAP+∠PAB=∠PAB+∠BAC,
即∠QAB=∠PAC.
在△ABQ和△ACP中,
∵AQ=AP,∠QAB=∠PAC,AB=AC,
∴△ABQ≌△ACP,∴BQ=CP.
