第14章 勾股定理 14.1 2.直角三角形的判定 同步练习 2021—2022学年华东师大版数八年级学上册(word版含答案)
文档属性
| 名称 | 第14章 勾股定理 14.1 2.直角三角形的判定 同步练习 2021—2022学年华东师大版数八年级学上册(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 117.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-03 11:54:20 | ||
图片预览



文档简介
14.1
2.直角三角形的判定
一、选择题
1.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
A.∠A是直角
B.∠B是直角
C.∠C是直角
D.△ABC不是直角三角形
2.下列说法中正确的有
( )
①如果∠A+∠B=∠C,那么△ABC是直角三角形;②如果∠A∶∠B∶∠C=1∶2∶3,那么△ABC是直角三角形;③如果三角形的三边长分别为4,4,6,那么这个三角形不是直角三角形;④有一个角是直角的三角形是直角三角形.
A.1个
B.2个
C.3个
D.4个
3.下列四组数中,可以作为直角三角形三边长的有
( )
(1)9,12,15;(2)7,24,25;(3)9,16,25;(4)3a,4a,5a(a>0).
A.4组
B.3组
C.2组
D.1组
4.已知三角形两边的长分别为3和5,要使这个三角形为直角三角形,则第三边的长应该为
( )
A.4
B.
C.4或
D.8
5.若△ABC的三边长分别为a,b,c,且满足等式(a+b)2-c2=2ab,则此三角形是
( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
6.若三角形的三边长分别是6,8,10,则它最长边上的高为
( )
A.6
B.2.4
C.8
D.4.8
7.如图1,在由边长为1的小正方形组成的网格中,△ABC的顶点都在格点上,则△ABC的形状为
( )
图1
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上选项都不对
8.甲、乙两艘客轮同时离开港口,航行的速度都是40
m/min,甲客轮航行15
min到达点A,乙客轮航行20
min到达点B.若A,B两点的直线距离为1000
m,甲客轮沿北偏东30°的方向航行,则乙客轮的航行方向可能是
( )
A.南偏东60°
B.南偏西30°
C.北偏西30°
D.南偏西60°
二、填空题
9.有五根木棍,它们的长分别为3,4,5,12,13,取其中的三根木棍搭成直角三角形,其取法有_____种.
10.已知代数式|x-12|+(y-13)2与z2-10z+25的值互为相反数,则以x,y,z为边长的三角形是_______三角形.?
11.如图2,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为 .?
图2
12.[2019·北京]
如图3所示的网格是正方形网格,则∠PAB+∠PBA= °(点A,B,P是网格线的交点).?
图3
三、解答题
13.已知a,b,c是△ABC的三边长,且a+b+c=60
cm,a∶b∶c=3∶4∶5,求△ABC的面积.
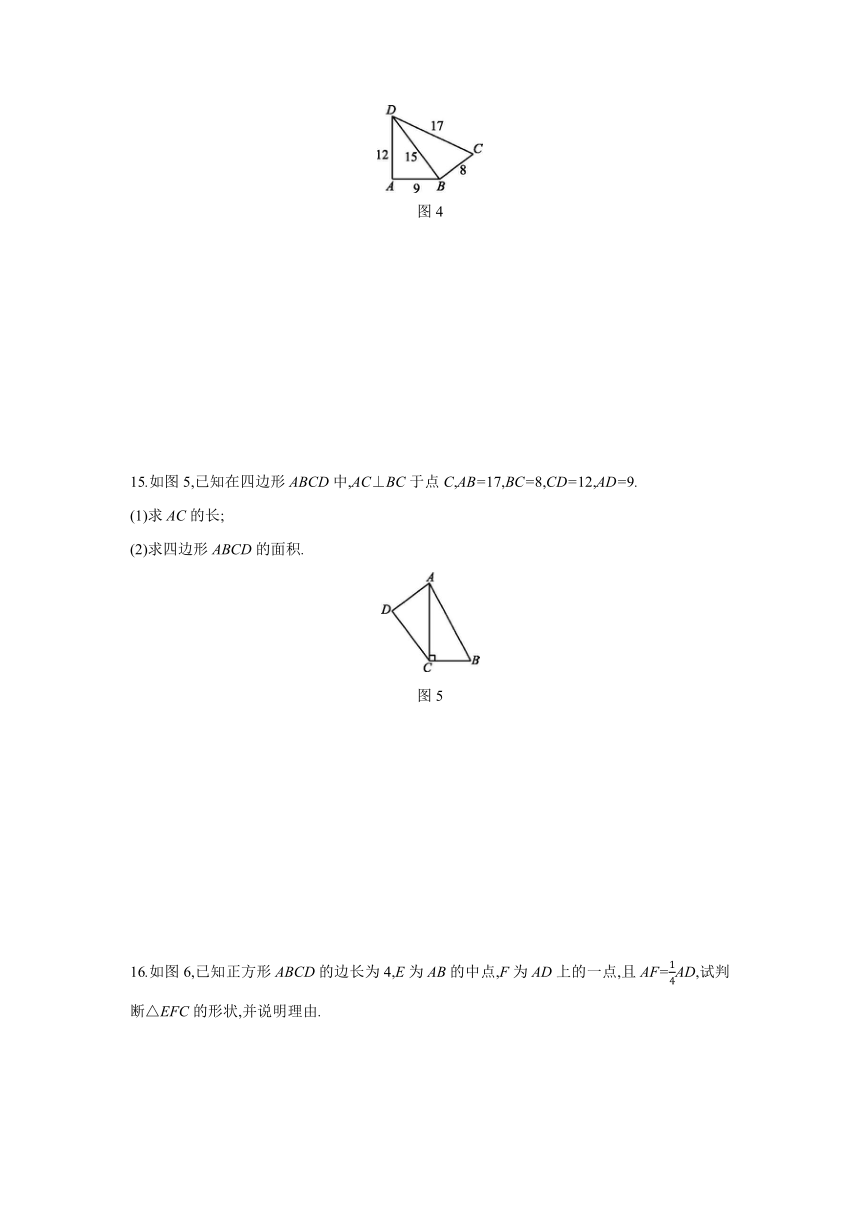
14.一种机器零件的形状如图4所示,按规定,这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如图所示,这个零件符合要求吗?请说明理由.
图4
15.如图5,已知在四边形ABCD中,AC⊥BC于点C,AB=17,BC=8,CD=12,AD=9.
(1)求AC的长;
(2)求四边形ABCD的面积.
图5
16.如图6,已知正方形ABCD的边长为4,E为AB的中点,F为AD上的一点,且AF=AD,试判断△EFC的形状,并说明理由.
图6
17.如图7所示是一块地,其中∠ADC=90°,AD=12
m,CD=9
m,AB=39
m,BC=36
m,求这块地的面积.
图7
18.如图8,在△ABC中,AB∶BC∶AC=3∶4∶5,且周长为36
cm,点P从点A开始沿AB边向点B以每秒1
cm的速度移动,点Q从点B开始沿BC边向点C以每秒2
cm的速度移动,如果两点同时出发,当运动时间为3
s时,△PBQ的面积为多少?
图8
答案
1.C 2.D
3.[解析]
B 在所给的4组数中,分别以(1)(2)(4)中的3个数为边长可以构成直角三角形.
4.[解析]
C 长为5的边可能是直角边,也可能是斜边.
5.[解析]
B ∵(a+b)2-c2=a2+b2+2ab-c2=2ab,∴a2+b2=c2,∴这个三角形是直角三角形.
6.[解析]
D ∵三角形的三边长分别为6,8,10,且62+82=102,
∴此三角形为直角三角形,且10为直角三角形的斜边长.
设三角形最长边上的高是h,
根据三角形的面积公式,得×6×8=×10h,
解得h=4.8.
7.[解析]
B 由勾股定理,得AC2=22+32=13,AB2=42+62=52,BC2=12+82=65,
则AC2+AB2=BC2,∴△ABC为直角三角形.
8.A 9.2 10.直角
11.[答案]
14
[解析]
由AD2+BD2=AB2,可知△ABD为直角三角形,且∠ADB=90°,则∠ADC=90°.在Rt△ACD中,由勾股定理,得CD2=AC2-AD2=152-122=81,所以CD=9,则BC=BD+CD=5+9=14.
12.[答案]
45
[解析]
如图,延长AP交网格于格点D,连结BD,
PD2=BD2=12+22=5,PB2=12+32=10,∴PD2+DB2=PB2,
∴∠PDB=90°,∴∠DPB=∠PAB+∠PBA=45°.故答案为45.
13.解:∵a+b+c=60
cm,a∶b∶c=3∶4∶5,
∴a=15
cm,b=20
cm,c=25
cm.
∵152+202=252,∴△ABC是直角三角形,
∴△ABC的面积为×15×20=150(cm2).
14.解:符合要求.理由:∵152=122+92,
∴BD2=AD2+AB2,
∴△ABD是直角三角形,且∠A=90°.
∵172=152+82,∴CD2=BD2+BC2,
∴△BCD是直角三角形,且∠DBC=90°,故这个零件符合要求.
15.解:(1)∵AC⊥BC,∴∠ACB=90°,
∴AC2=AB2-BC2=172-82=225,
∴AC=15.
(2)∵AD2+CD2=92+122=225=AC2,
∴△ACD是直角三角形,且∠D=90°,
∴S四边形ABCD=S△ABC+S△ACD=×8×15+×12×9=114.
16.解:△EFC是直角三角形.理由如下:
∵E为AB的中点,AB=4,
∴AE=BE=2,
∴CE2=BE2+BC2=22+42=20.
∵AF=AD,
∴AF=1,则DF=AD-AF=3,
∴EF2=AE2+AF2=22+12=5,
CF2=DF2+CD2=32+42=25,
∴CE2+EF2=CF2,
∴△EFC是直角三角形.
17.解:连结AC.
在Rt△ADC中,根据勾股定理,
得AC===15(m).
又∵AC2+BC2=152+362=1521,
AB2=392=1521,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°,
∴这块地的面积=S△ABC-S△ADC=AC·BC-AD·CD=×15×36-×12×9=216(m2).
故这块地的面积为216
m2.
18.解:根据题意,设AB=3x
cm,BC=4x
cm,AC=5x
cm.
∵△ABC的周长为36
cm,
∴AB+BC+AC=36
cm,
即3x+4x+5x=36,解得x=3,
∴AB=9
cm,BC=12
cm,AC=15
cm,
∴AB2+BC2=AC2,
∴△ABC是直角三角形,且∠B=90°.
当运动时间为3
s时,BP=9-3×1=6(cm),BQ=2×3=6(cm),
∴S△PBQ=BP·BQ=×6×6=18(cm2).
故当运动时间为3
s时,△PBQ的面积为18
cm2.
2.直角三角形的判定
一、选择题
1.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
A.∠A是直角
B.∠B是直角
C.∠C是直角
D.△ABC不是直角三角形
2.下列说法中正确的有
( )
①如果∠A+∠B=∠C,那么△ABC是直角三角形;②如果∠A∶∠B∶∠C=1∶2∶3,那么△ABC是直角三角形;③如果三角形的三边长分别为4,4,6,那么这个三角形不是直角三角形;④有一个角是直角的三角形是直角三角形.
A.1个
B.2个
C.3个
D.4个
3.下列四组数中,可以作为直角三角形三边长的有
( )
(1)9,12,15;(2)7,24,25;(3)9,16,25;(4)3a,4a,5a(a>0).
A.4组
B.3组
C.2组
D.1组
4.已知三角形两边的长分别为3和5,要使这个三角形为直角三角形,则第三边的长应该为
( )
A.4
B.
C.4或
D.8
5.若△ABC的三边长分别为a,b,c,且满足等式(a+b)2-c2=2ab,则此三角形是
( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
6.若三角形的三边长分别是6,8,10,则它最长边上的高为
( )
A.6
B.2.4
C.8
D.4.8
7.如图1,在由边长为1的小正方形组成的网格中,△ABC的顶点都在格点上,则△ABC的形状为
( )
图1
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上选项都不对
8.甲、乙两艘客轮同时离开港口,航行的速度都是40
m/min,甲客轮航行15
min到达点A,乙客轮航行20
min到达点B.若A,B两点的直线距离为1000
m,甲客轮沿北偏东30°的方向航行,则乙客轮的航行方向可能是
( )
A.南偏东60°
B.南偏西30°
C.北偏西30°
D.南偏西60°
二、填空题
9.有五根木棍,它们的长分别为3,4,5,12,13,取其中的三根木棍搭成直角三角形,其取法有_____种.
10.已知代数式|x-12|+(y-13)2与z2-10z+25的值互为相反数,则以x,y,z为边长的三角形是_______三角形.?
11.如图2,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为 .?
图2
12.[2019·北京]
如图3所示的网格是正方形网格,则∠PAB+∠PBA= °(点A,B,P是网格线的交点).?
图3
三、解答题
13.已知a,b,c是△ABC的三边长,且a+b+c=60
cm,a∶b∶c=3∶4∶5,求△ABC的面积.
14.一种机器零件的形状如图4所示,按规定,这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如图所示,这个零件符合要求吗?请说明理由.
图4
15.如图5,已知在四边形ABCD中,AC⊥BC于点C,AB=17,BC=8,CD=12,AD=9.
(1)求AC的长;
(2)求四边形ABCD的面积.
图5
16.如图6,已知正方形ABCD的边长为4,E为AB的中点,F为AD上的一点,且AF=AD,试判断△EFC的形状,并说明理由.
图6
17.如图7所示是一块地,其中∠ADC=90°,AD=12
m,CD=9
m,AB=39
m,BC=36
m,求这块地的面积.
图7
18.如图8,在△ABC中,AB∶BC∶AC=3∶4∶5,且周长为36
cm,点P从点A开始沿AB边向点B以每秒1
cm的速度移动,点Q从点B开始沿BC边向点C以每秒2
cm的速度移动,如果两点同时出发,当运动时间为3
s时,△PBQ的面积为多少?
图8
答案
1.C 2.D
3.[解析]
B 在所给的4组数中,分别以(1)(2)(4)中的3个数为边长可以构成直角三角形.
4.[解析]
C 长为5的边可能是直角边,也可能是斜边.
5.[解析]
B ∵(a+b)2-c2=a2+b2+2ab-c2=2ab,∴a2+b2=c2,∴这个三角形是直角三角形.
6.[解析]
D ∵三角形的三边长分别为6,8,10,且62+82=102,
∴此三角形为直角三角形,且10为直角三角形的斜边长.
设三角形最长边上的高是h,
根据三角形的面积公式,得×6×8=×10h,
解得h=4.8.
7.[解析]
B 由勾股定理,得AC2=22+32=13,AB2=42+62=52,BC2=12+82=65,
则AC2+AB2=BC2,∴△ABC为直角三角形.
8.A 9.2 10.直角
11.[答案]
14
[解析]
由AD2+BD2=AB2,可知△ABD为直角三角形,且∠ADB=90°,则∠ADC=90°.在Rt△ACD中,由勾股定理,得CD2=AC2-AD2=152-122=81,所以CD=9,则BC=BD+CD=5+9=14.
12.[答案]
45
[解析]
如图,延长AP交网格于格点D,连结BD,
PD2=BD2=12+22=5,PB2=12+32=10,∴PD2+DB2=PB2,
∴∠PDB=90°,∴∠DPB=∠PAB+∠PBA=45°.故答案为45.
13.解:∵a+b+c=60
cm,a∶b∶c=3∶4∶5,
∴a=15
cm,b=20
cm,c=25
cm.
∵152+202=252,∴△ABC是直角三角形,
∴△ABC的面积为×15×20=150(cm2).
14.解:符合要求.理由:∵152=122+92,
∴BD2=AD2+AB2,
∴△ABD是直角三角形,且∠A=90°.
∵172=152+82,∴CD2=BD2+BC2,
∴△BCD是直角三角形,且∠DBC=90°,故这个零件符合要求.
15.解:(1)∵AC⊥BC,∴∠ACB=90°,
∴AC2=AB2-BC2=172-82=225,
∴AC=15.
(2)∵AD2+CD2=92+122=225=AC2,
∴△ACD是直角三角形,且∠D=90°,
∴S四边形ABCD=S△ABC+S△ACD=×8×15+×12×9=114.
16.解:△EFC是直角三角形.理由如下:
∵E为AB的中点,AB=4,
∴AE=BE=2,
∴CE2=BE2+BC2=22+42=20.
∵AF=AD,
∴AF=1,则DF=AD-AF=3,
∴EF2=AE2+AF2=22+12=5,
CF2=DF2+CD2=32+42=25,
∴CE2+EF2=CF2,
∴△EFC是直角三角形.
17.解:连结AC.
在Rt△ADC中,根据勾股定理,
得AC===15(m).
又∵AC2+BC2=152+362=1521,
AB2=392=1521,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°,
∴这块地的面积=S△ABC-S△ADC=AC·BC-AD·CD=×15×36-×12×9=216(m2).
故这块地的面积为216
m2.
18.解:根据题意,设AB=3x
cm,BC=4x
cm,AC=5x
cm.
∵△ABC的周长为36
cm,
∴AB+BC+AC=36
cm,
即3x+4x+5x=36,解得x=3,
∴AB=9
cm,BC=12
cm,AC=15
cm,
∴AB2+BC2=AC2,
∴△ABC是直角三角形,且∠B=90°.
当运动时间为3
s时,BP=9-3×1=6(cm),BQ=2×3=6(cm),
∴S△PBQ=BP·BQ=×6×6=18(cm2).
故当运动时间为3
s时,△PBQ的面积为18
cm2.
