7.3.2正弦型函数的性质与图像 教案-2021-2022学年高一下学期数学人教B版(2019)必修第三册
文档属性
| 名称 | 7.3.2正弦型函数的性质与图像 教案-2021-2022学年高一下学期数学人教B版(2019)必修第三册 |

|
|
| 格式 | docx | ||
| 文件大小 | 113.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-02 00:00:00 | ||
图片预览




文档简介
7.3.2正弦型函数的性质与图像教案
教学课时:1课时
教学目标:
1、能根据解析式总结y=Asinx(A>0)、y=sin(x+φ)、y=sinωx(ω>0)、y=Asin(ωx+φ)的性质;
2、能用五点法作上述函数的简图。通过作图过程明确A、ω、φ对函数性质与图像的影响,概括出三角函数图像变换的实质和规律,并用图象变换画出函数y=Asin(ωx+φ)的图像;
3、结合观览车和弹簧实例,体会y=Asin(ωx+φ)这类函数模型与生活的联系,了解A、ω、φ的实际意义及周期、频率、初相的定义;
4、通过对探索过程的体验,培养观察能力和探索问题的能力,体会数形结合以及从特殊到一般的数学思想,锻炼从具体到抽象的思维方法,达到从感性认识到理性认识的飞跃.
教学重点:
A、ω、φ对函数性质与图像的影响及y=sinx的图像到y=Asin(ωx+φ)的图像变换过程.
教学难点:
y=sinx的图像到y=Asin(ωx+φ)的图像的变换过程.
教学过程:
一、创设情境、引出问题
问题1:如图,摩天轮圆C的半径为A,为圆C上一点,以射线C为终边的角为φ,点P从出发随着时间推移而逆时针运动,P点每秒转过的弧度为ω,记圆心C的高度为0.,你能用一个合适的函数模型刻画的高度y与时间x的关系吗?
【教师活动】用GGB展示摩天轮,提出问题1,先引导学生思考当φ=0时的纵坐标y,再将移动到图示所示位置,求y.
【学生活动】当φ=0,由正弦函数的定义,得到y=Asinωx;将置于如图所示位置,得到在时刻x秒时点P的纵坐标y=Asin(ωx+φ).
问题2:y=Asin(ωx+φ)图像与学过的哪个函数图像相似?它们有何关系?
【教师活动】用GGB动态展示纵坐标y随x变化形成的函数y=Asin(ωx+φ)图像,生活中的许多现象,例如弹簧振子在振动过程中离开平衡位置的位移,潮汐现象中水位的高度也是这类函数模型的应用,前面我们已经学习了正弦函数的性质与图像,今天我们就一起来探究正弦型函数y=Asin(ωx+φ)的性质与图像.
【学生活动】学生观察图像,回答老师问题.学生回答,和正弦函数相似.y=sinx就是y=Asin(ωx+φ)在A=1,ω=1,φ=0时的情况.
【设计意图】用数学的眼光观察世界,感悟函数y=Asin(ωx+φ)是刻画自然界周期现象的常见的数学模型,体会函数与生活的紧密联系,引导学生思考y=Asin(ωx+φ)与y=sinx的一般与特殊的关系.
二、自主建构,解决问题
问题1:你打算如何研究y=Asin(ωx+φ)的性质与图像?
【教师活动】用ppt展示y=Asin(ωx+φ)的图像,教师引导学生通过比较发现y=Asin(ωx+φ)的图像与正弦曲线形状很相似,但也有区别,引导学生思考如何分析参数A、ω、φ的影响.
【学生活动】先固定其中的两个,研究另外一个参数对函数性质与图像的影响,分别探讨函数y=Asinx(A>0)、y=sin(x+φ)、y=sinωx(ω>0)的性质与图象,再综合分析.
问题2:探究y=2sinx的定义域、值域和周期,并作出它在一个周期内的图像.
【教师活动】教师提出问题,引导学生比较y=2sinx与y=sinx的性质,发现最值不同,引出下一问题.
【学生活动】学生分析解析式得到函数性质,通过五点法作出函数图像.
问题3:y=2sinx的图像如何由y=sinx的图像得到?
【教师活动】教师引导学生结合五点法作图的表格找到两个函数的联系,可以提示同学们观察的关系.
【学生活动】通过五点法的作图过程,比较两个函数图像的关键点,可以发现横坐标不变,纵坐标变为原来的2倍.
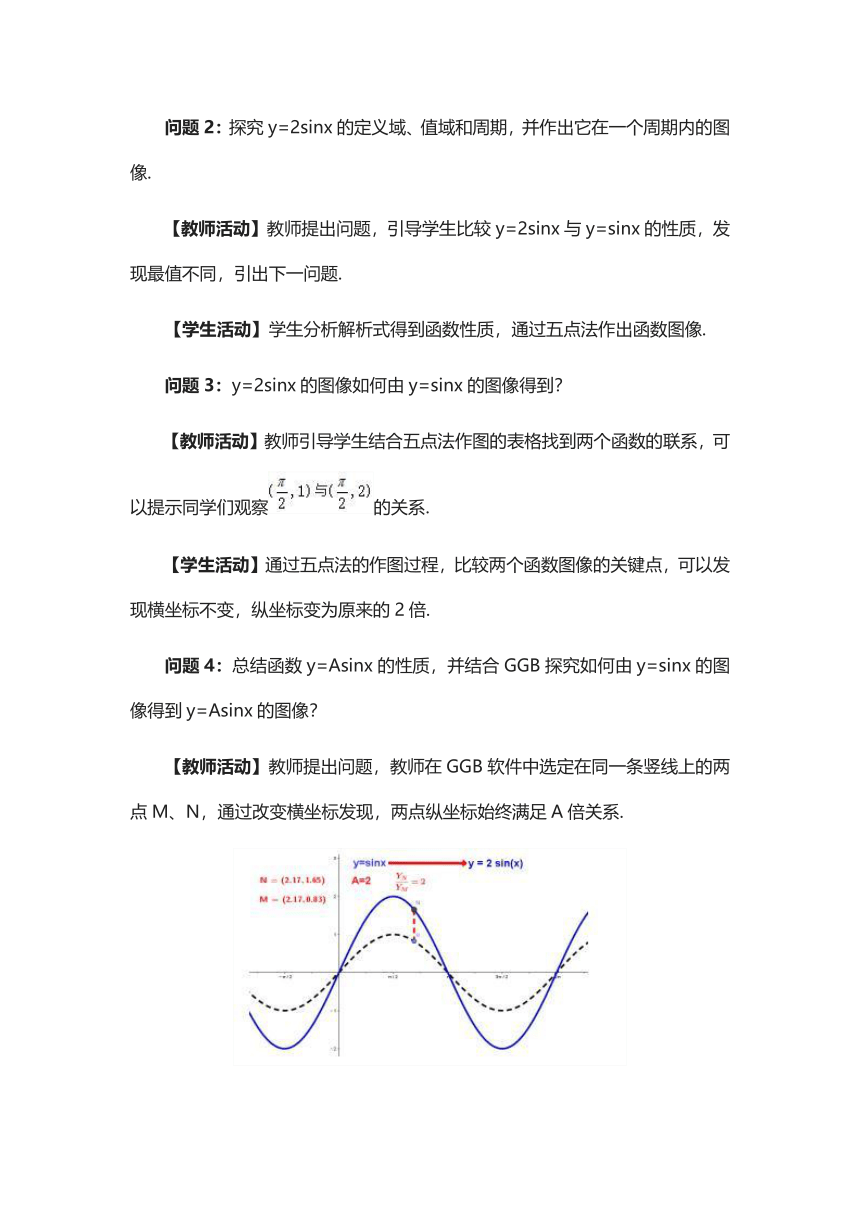
问题4:总结函数y=Asinx的性质,并结合GGB探究如何由y=sinx的图像得到y=Asinx的图像?
【教师活动】教师提出问题,教师在GGB软件中选定在同一条竖线上的两点M、N,通过改变横坐标发现,两点纵坐标始终满足A倍关系.
【学生活动】学生总结出函数y=Asinx的性质,定义域:R值域:[-A,A]
周期2π,通过平板操作GGB软件改变参数A的大小,通过观察点坐标的联系,分析得出函数图像之间的关系如下:
【设计意图】本环节将需要解决的三个参数进行分解,先逐个分析参数对图像的影响,从参数A入手,引导学生从特殊到一般分析A对函数性质与图像的影响,探究过程中,借助GGB的动态展示,合理的展现了探究结论的过程,较好的突破了探究难点,激发了学生的探究欲望,提高了学生分析问题、解决问题的能力.
三、类比方法,合作探究
问题1:总结y=sin(x+φ)的性质,并探究如何由y=sinx的图像得到y=sin(x+φ)的图像?
【教师活动】引导学生通过换元的方法分析y=sin(x+φ)的性质,再借助GGB演示当φ变化时图像的变化情况,提问学生图像的变化规律.
【学生活动】学生先总结y=sin(x+φ)的性质,再借助GGB进行数学实验,发现φ引起的是图像x轴方向的平移变换,规律为左加右减,总结出一般规律如下:
问题2:总结y=sin(ωx)的性质,并探究如何由y=sinx的图像得到y=sin(ωx)的图像?
【教师活动】在分析函数周期时,教师要提醒学生从周期的定义出发,找到x的改变量为多少时,函数值重复出现,再引导学生借助GGB的动态演示功能,结合点坐标的变化,找到ω变化时图像的变化规律.
【学生活动】学生类比之前的方法自主探究y=sin(ωx)的性质,发现ω与周期成反比的规律,总结出,借助GGB进行数学实验,发现ω引起的是图像x轴方向的伸缩变换,观察出ω越大,周期越小,验证了分析函数性质时得到的结论,得到图像变换如下的结论:
【设计意图】由具体到抽象,类比上一环节的探究过程,继续探究φ、ω对函数性质与图像的影响,图像变换的本质是图像上每个点的位置变化,而点的位置变化对应了点的坐标的变化,此处不仅从形的角度认识规律,更加突出从点的坐标这一数的本质去理解,实现思维水平的提升.
四、综合应用、深化提升
问题1:探究的定义域、值域和周期,并用五点法做出它在一个周期内的图像.
【教师活动】教师提出问题,引导学生思考,能否用前面的方法分析函数的性质?作图时的五点如何选择?除了五点法作图,我们还可以用什么方法得到图像?引出下一问题.
【学生活动】学生用整体分析的方法分析函数性质和五点作图,此外可以由y=sinx通过图像变换的方法得到图像.
问题2:如何由函数y=sinx的图像变成的图像?
【教师活动】教师提出问题,引导学生通过对比两个函数的性质与图像,提出综合应用图像变换的方案,用ppt分步骤展示图像的变换过程,对图像变换的难点和易错点,提醒学生对比图像坐标进行分析,通过引导学生发现和提出问题,激发学生的学习兴趣.
【学生活动】结合与y=sinx的函数性质,并观察五点法作出的图像,提出不同方案:先伸缩后平移,先平移后伸缩.学生在先伸缩后平移时,可能会认为是左移个单位长度,但是通过分析点坐标的变化最后发现这样做是错误的,从而激发他们求知欲,加深对图像变换的理解,第二种变换的难点在伸缩变化中,φ是否受到影响,同样从本质出发,通过分析点的变化来理解,最后结合GGB来验证.
巩固练习:1.如何由函数y=sinx的图像变成的图像?
2.如何由函数的图像变成的图像?
【教师活动】教师用ppt投影展示问题,随机提问两个小组回答。
【学生活动】学生独立思考,再小组讨论,比较不同的图像变换方案,加深对图像变换的理解。
问题3:总结y=Asin(ωx+φ)的定义域、值域、周期,并思考A、ω、φ有怎样的实际意义?
【教师活动】教师提出问题,提问一名学生总结性质,并用GGB回顾摩天轮和弹簧产生正弦型函数的过程,结合本节课对参数A、ω、φ的研究,总结三个参数的实际意义.
【学生活动】学生独立思考,由特殊到一般总结y=Asin(ωx+φ)的性质,联系实际得到三个参数的实际意义.
【设计意图】本环节是图像变换的综合应用,通过对比两个函数的性质与图像,提出方案,遇到问题时,先从本质出发通过分析点坐标的变化,从而解决问题,借助GGB软件,既能直观判断能否完成图像的合理变换,亦能找出是否合理的原因,使学生从感性和理性两个角度认识到变换的过程,最后,由特殊到一般,总结正弦型函数的性质及图像,联系实际,体现出数学既来自于生活,也服务于生活.
五、归纳总结,反思提高
问题:本节课你收获了什么?
1.
y=Asin(ωx+φ)的性质与图像及A、ω、φ的实际意义;
2.
y=sinx的图像变成y=Asin(ωx+φ)的图像的步骤.
【教师活动】教师提出问题,指定一名同学进行回答,在学生回答过程中进行引导和评价,通过激励性评价,提高学生的学习热情.
【学生活动】学生对本节课所学的知识与方法进行总结,一名同学回答问题,其他同学进行必要的补充.
【设计意图】引导学生对所学的知识、数学思想方法进行小结,培养学生的概括、归纳能力,从而为今后的学习打下坚实的基础.
教学课时:1课时
教学目标:
1、能根据解析式总结y=Asinx(A>0)、y=sin(x+φ)、y=sinωx(ω>0)、y=Asin(ωx+φ)的性质;
2、能用五点法作上述函数的简图。通过作图过程明确A、ω、φ对函数性质与图像的影响,概括出三角函数图像变换的实质和规律,并用图象变换画出函数y=Asin(ωx+φ)的图像;
3、结合观览车和弹簧实例,体会y=Asin(ωx+φ)这类函数模型与生活的联系,了解A、ω、φ的实际意义及周期、频率、初相的定义;
4、通过对探索过程的体验,培养观察能力和探索问题的能力,体会数形结合以及从特殊到一般的数学思想,锻炼从具体到抽象的思维方法,达到从感性认识到理性认识的飞跃.
教学重点:
A、ω、φ对函数性质与图像的影响及y=sinx的图像到y=Asin(ωx+φ)的图像变换过程.
教学难点:
y=sinx的图像到y=Asin(ωx+φ)的图像的变换过程.
教学过程:
一、创设情境、引出问题
问题1:如图,摩天轮圆C的半径为A,为圆C上一点,以射线C为终边的角为φ,点P从出发随着时间推移而逆时针运动,P点每秒转过的弧度为ω,记圆心C的高度为0.,你能用一个合适的函数模型刻画的高度y与时间x的关系吗?
【教师活动】用GGB展示摩天轮,提出问题1,先引导学生思考当φ=0时的纵坐标y,再将移动到图示所示位置,求y.
【学生活动】当φ=0,由正弦函数的定义,得到y=Asinωx;将置于如图所示位置,得到在时刻x秒时点P的纵坐标y=Asin(ωx+φ).
问题2:y=Asin(ωx+φ)图像与学过的哪个函数图像相似?它们有何关系?
【教师活动】用GGB动态展示纵坐标y随x变化形成的函数y=Asin(ωx+φ)图像,生活中的许多现象,例如弹簧振子在振动过程中离开平衡位置的位移,潮汐现象中水位的高度也是这类函数模型的应用,前面我们已经学习了正弦函数的性质与图像,今天我们就一起来探究正弦型函数y=Asin(ωx+φ)的性质与图像.
【学生活动】学生观察图像,回答老师问题.学生回答,和正弦函数相似.y=sinx就是y=Asin(ωx+φ)在A=1,ω=1,φ=0时的情况.
【设计意图】用数学的眼光观察世界,感悟函数y=Asin(ωx+φ)是刻画自然界周期现象的常见的数学模型,体会函数与生活的紧密联系,引导学生思考y=Asin(ωx+φ)与y=sinx的一般与特殊的关系.
二、自主建构,解决问题
问题1:你打算如何研究y=Asin(ωx+φ)的性质与图像?
【教师活动】用ppt展示y=Asin(ωx+φ)的图像,教师引导学生通过比较发现y=Asin(ωx+φ)的图像与正弦曲线形状很相似,但也有区别,引导学生思考如何分析参数A、ω、φ的影响.
【学生活动】先固定其中的两个,研究另外一个参数对函数性质与图像的影响,分别探讨函数y=Asinx(A>0)、y=sin(x+φ)、y=sinωx(ω>0)的性质与图象,再综合分析.
问题2:探究y=2sinx的定义域、值域和周期,并作出它在一个周期内的图像.
【教师活动】教师提出问题,引导学生比较y=2sinx与y=sinx的性质,发现最值不同,引出下一问题.
【学生活动】学生分析解析式得到函数性质,通过五点法作出函数图像.
问题3:y=2sinx的图像如何由y=sinx的图像得到?
【教师活动】教师引导学生结合五点法作图的表格找到两个函数的联系,可以提示同学们观察的关系.
【学生活动】通过五点法的作图过程,比较两个函数图像的关键点,可以发现横坐标不变,纵坐标变为原来的2倍.
问题4:总结函数y=Asinx的性质,并结合GGB探究如何由y=sinx的图像得到y=Asinx的图像?
【教师活动】教师提出问题,教师在GGB软件中选定在同一条竖线上的两点M、N,通过改变横坐标发现,两点纵坐标始终满足A倍关系.
【学生活动】学生总结出函数y=Asinx的性质,定义域:R值域:[-A,A]
周期2π,通过平板操作GGB软件改变参数A的大小,通过观察点坐标的联系,分析得出函数图像之间的关系如下:
【设计意图】本环节将需要解决的三个参数进行分解,先逐个分析参数对图像的影响,从参数A入手,引导学生从特殊到一般分析A对函数性质与图像的影响,探究过程中,借助GGB的动态展示,合理的展现了探究结论的过程,较好的突破了探究难点,激发了学生的探究欲望,提高了学生分析问题、解决问题的能力.
三、类比方法,合作探究
问题1:总结y=sin(x+φ)的性质,并探究如何由y=sinx的图像得到y=sin(x+φ)的图像?
【教师活动】引导学生通过换元的方法分析y=sin(x+φ)的性质,再借助GGB演示当φ变化时图像的变化情况,提问学生图像的变化规律.
【学生活动】学生先总结y=sin(x+φ)的性质,再借助GGB进行数学实验,发现φ引起的是图像x轴方向的平移变换,规律为左加右减,总结出一般规律如下:
问题2:总结y=sin(ωx)的性质,并探究如何由y=sinx的图像得到y=sin(ωx)的图像?
【教师活动】在分析函数周期时,教师要提醒学生从周期的定义出发,找到x的改变量为多少时,函数值重复出现,再引导学生借助GGB的动态演示功能,结合点坐标的变化,找到ω变化时图像的变化规律.
【学生活动】学生类比之前的方法自主探究y=sin(ωx)的性质,发现ω与周期成反比的规律,总结出,借助GGB进行数学实验,发现ω引起的是图像x轴方向的伸缩变换,观察出ω越大,周期越小,验证了分析函数性质时得到的结论,得到图像变换如下的结论:
【设计意图】由具体到抽象,类比上一环节的探究过程,继续探究φ、ω对函数性质与图像的影响,图像变换的本质是图像上每个点的位置变化,而点的位置变化对应了点的坐标的变化,此处不仅从形的角度认识规律,更加突出从点的坐标这一数的本质去理解,实现思维水平的提升.
四、综合应用、深化提升
问题1:探究的定义域、值域和周期,并用五点法做出它在一个周期内的图像.
【教师活动】教师提出问题,引导学生思考,能否用前面的方法分析函数的性质?作图时的五点如何选择?除了五点法作图,我们还可以用什么方法得到图像?引出下一问题.
【学生活动】学生用整体分析的方法分析函数性质和五点作图,此外可以由y=sinx通过图像变换的方法得到图像.
问题2:如何由函数y=sinx的图像变成的图像?
【教师活动】教师提出问题,引导学生通过对比两个函数的性质与图像,提出综合应用图像变换的方案,用ppt分步骤展示图像的变换过程,对图像变换的难点和易错点,提醒学生对比图像坐标进行分析,通过引导学生发现和提出问题,激发学生的学习兴趣.
【学生活动】结合与y=sinx的函数性质,并观察五点法作出的图像,提出不同方案:先伸缩后平移,先平移后伸缩.学生在先伸缩后平移时,可能会认为是左移个单位长度,但是通过分析点坐标的变化最后发现这样做是错误的,从而激发他们求知欲,加深对图像变换的理解,第二种变换的难点在伸缩变化中,φ是否受到影响,同样从本质出发,通过分析点的变化来理解,最后结合GGB来验证.
巩固练习:1.如何由函数y=sinx的图像变成的图像?
2.如何由函数的图像变成的图像?
【教师活动】教师用ppt投影展示问题,随机提问两个小组回答。
【学生活动】学生独立思考,再小组讨论,比较不同的图像变换方案,加深对图像变换的理解。
问题3:总结y=Asin(ωx+φ)的定义域、值域、周期,并思考A、ω、φ有怎样的实际意义?
【教师活动】教师提出问题,提问一名学生总结性质,并用GGB回顾摩天轮和弹簧产生正弦型函数的过程,结合本节课对参数A、ω、φ的研究,总结三个参数的实际意义.
【学生活动】学生独立思考,由特殊到一般总结y=Asin(ωx+φ)的性质,联系实际得到三个参数的实际意义.
【设计意图】本环节是图像变换的综合应用,通过对比两个函数的性质与图像,提出方案,遇到问题时,先从本质出发通过分析点坐标的变化,从而解决问题,借助GGB软件,既能直观判断能否完成图像的合理变换,亦能找出是否合理的原因,使学生从感性和理性两个角度认识到变换的过程,最后,由特殊到一般,总结正弦型函数的性质及图像,联系实际,体现出数学既来自于生活,也服务于生活.
五、归纳总结,反思提高
问题:本节课你收获了什么?
1.
y=Asin(ωx+φ)的性质与图像及A、ω、φ的实际意义;
2.
y=sinx的图像变成y=Asin(ωx+φ)的图像的步骤.
【教师活动】教师提出问题,指定一名同学进行回答,在学生回答过程中进行引导和评价,通过激励性评价,提高学生的学习热情.
【学生活动】学生对本节课所学的知识与方法进行总结,一名同学回答问题,其他同学进行必要的补充.
【设计意图】引导学生对所学的知识、数学思想方法进行小结,培养学生的概括、归纳能力,从而为今后的学习打下坚实的基础.
