上海市虹口区2020-2021学年高二下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 上海市虹口区2020-2021学年高二下学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 703.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-02 22:10:54 | ||
图片预览



文档简介
虹口区高二期末数学试卷
2021.06.
一?填空题
1.已知集合false,则false__________.
2.设false,若复数false是纯虚数,则false__________.
3.不等式false的解集为__________.
4.在false的二项展开式中,常数项是__________.(用数字作答)
5.已知圆锥的主视图为如图所示,则该圆锥的侧面积是__________.
6.已知复数false满足false,则false的取值范围是__________.
7.我校4位同学报考了某大学“强基计划”第1专业组,并顺利通过各项考核,已知4位同学将根据综合成绩和志愿顺序随机地进入数学类?物理学类?计算机类这三个专业中的某一个专业,则这三个专业都有我校学生的录取方法总数有__________种(用数字作答).
8.一个三位数,个位?十位?百位上的数字依次为false,当且仅当false时,称这样的数为“凸数”(如341),则从集合false中取出三个不相同的数组成的凸数个数为___________(用数字作答).
9.(A组题)若false,则false__________.
(B组题)若false,则false__________.
10.(A组题)已知正三棱柱false的侧棱长为4,底面边长为false,且它的六个顶点均在球false的球面上,则false两点的球面距离为__________.
(B组题)已知正三棱柱false的侧棱长为4,底面边长为false,且它的六个顶点均在球false的球面上,则球false的体积为__________.
二?选择题
11.“false”是“false”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
12.设false,且false,则( )
A.false B.false C.false D.false
13.正方体false中,false为线段false上的一个动点,则下列结论错误的是( )
A.false B.false平面false
C.三棱锥false的体积为定值 D.直线false直线false
14.已知false,则false的值不可能为( )
A.false B.false C.false D.false
15.(A组题)已知复数false满足false,复数false满足false或者false,且false对任意false成立,则正整数false的最大值( )
A.6 B.8 C.10 D.12
(B组题)对任意复数false,定义false,其中false是false的共轭复数,对任意复数false,有如下结论:
(1)false
(2)false
(3)false
(4)false
则正确结论的个数是( )
A.4 B.3 C.2 D.1
三?解答题
16.已知false.
(1)若false,求false;
(2)若“false”是“false”的充分不必要条件,求实数false的取值范围.
17.(1)在复数范围内解方程:false为虚数单位);
(2)已知系数为整数的一元二次方程false的一根为false,求false的最小值.
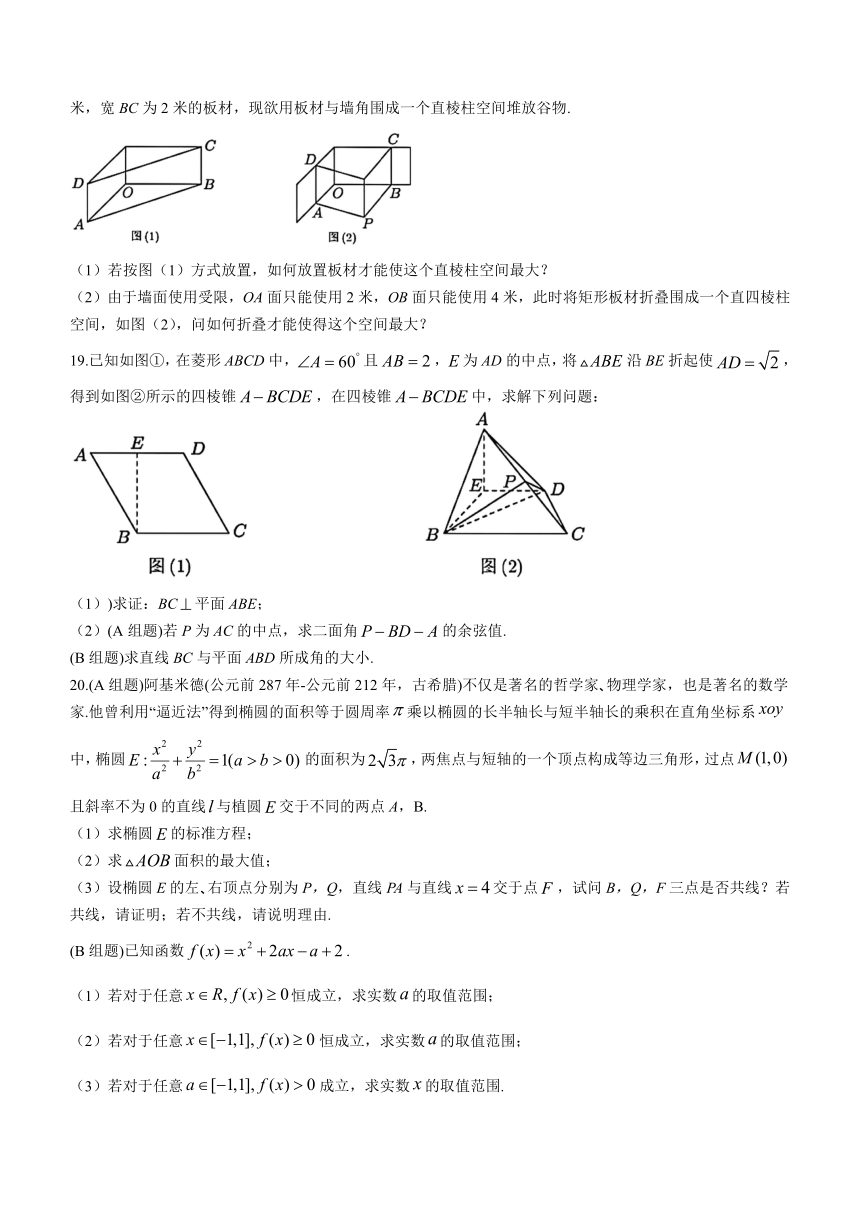
18.如图(1)是一直角墙角,false,墙角的两堵墙面和地面两两互相垂直,ABCD是一块长AB为6米,宽BC为2米的板材,现欲用板材与墙角围成一个直棱柱空间堆放谷物.
(1)若按图(1)方式放置,如何放置板材才能使这个直棱柱空间最大?
(2)由于墙面使用受限,OA面只能使用2米,OB面只能使用4米,此时将矩形板材折叠围成一个直四棱柱空间,如图(2),问如何折叠才能使得这个空间最大?
19.已知如图①,在菱形ABCD中,false且false,false为AD的中点,将false沿BE折起使false,得到如图②所示的四棱锥false,在四棱锥false中,求解下列问题:
(1))求证:BCfalse平面ABE;
(2)(A组题)若P为AC的中点,求二面角false的余弦值.
(B组题)求直线BC与平面ABD所成角的大小.
20.(A组题)阿基米德(公元前287年-公元前212年,古希腊)不仅是著名的哲学家?物理学家,也是著名的数学家.他曾利用“逼近法”得到椭圆的面积等于圆周率false乘以椭圆的长半轴长与短半轴长的乘积在直角坐标系false中,椭圆false的面积为false,两焦点与短轴的一个顶点构成等边三角形,过点false且斜率不为0的直线false与植圆false交于不同的两点A,B.
(1)求椭圆false的标准方程;
(2)求false面积的最大值;
(3)设椭圆E的左?右顶点分别为P,Q,直线PA与直线false交于点false,试问B,Q,F三点是否共线?若共线,请证明;若不共线,请说明理由.
(B组题)已知函数false.
(1)若对于任意false恒成立,求实数false的取值范围;
(2)若对于任意false恒成立,求实数false的取值范围;
(3)若对于任意false成立,求实数false的取值范围.
参考答案
1.false 2.2 3.false 4.20
5.false 6.false 7.36 8.20
9.(A组题)251;(B组题)252 10.(A组题)false;(B组题)false
11.A 12.D 13.D 14.A 15.(A组题)C;(B组题)C
16.(本题满分8分)本题共2小题,每小题4分.
解:(1)由条件,可得false.
当false时,false,故false.
(2)由于false的区间长度不相等,故当“false是false"
的充分不必要条件时,false
解得false,故实数m的取值范围为false
17.(本题满分10分)本题共2小题,每小题5分.
(1)设复数false,则原方程化为false
于是false,解得false
因此原方程的解为false,或falsei.
(2)由条件可得false
解得false,故false,又a,b,c均为整致,故false
因此false
18.(本题满分10分)本题共2小题,每小题5分.
解:(1)设false,则由条件,得false.
从而板材围成的直校柱空间的容积为false
由基本不等式,得false当且仅当false时,等号成立.
因此,放置板材使AOAB为等腰直角三角形,即false(米)时,围成的直梭柱空间的容积最大为18立方米.
(2)设false则由条件,得false
当false时false面积取最大值false
要使将矩形板材折叠围成的直四校柱空间最大,在false时,点P到边AB的距离必须是最大的,即false(M为AB的中点).
此时false
直四校柱空间的容积最大位为false(立方米)
19.(本题满分10分)本题共2小题,4小四5分.
证:(1)在图①中,述接BD,如图所示
因为四边形ABCD为变形.false,所以
false是等边三角形.
因为E为AD中点,所以false.
又false,所以false
在图②中,false,
所以false,即false
因为false,
所以false
又false均在平面false内.
所以false平面false
(2)(false组题)由(1)知,falseBCDE
以false为坐标原点,以射线false分别为false轴,false轴,false轴建立如图所示的空间直角坐标系,则false
false
设平面ABD的一个法向量为false
因为false
由false得false,令false,得false
设平面false的一个法向然为false,
因为false,
由false得false,
令false得false
解:(2)(B组题)由(1)知.false平面false
以E为坐标原点,以射线EB,ED,EA分别为x轴,y轴,z轴,建立如图所示的空间直
角坐标系,false.
false
设平面ABD的一个法向量为false
因为false,
由false得false,
令false,得false
设平面false的一个法向然为false,
因为false,
由false得false,
令false得false
因false,设直线false与平面false所戌角的大小为false,则
false
所以直线BC与平面ABD所成角的大小为false
20.(本题满分12分)(A组题,本题共3小愿,每小题4分)
(1)由题意可得:false,
解得false,false,false,
所以椭圆方程为false.
(2)设直线false的方程为false,false,false,
由false,整理得false,
false,
false,
令false(false),则false,
设false,函数false在区间false单调递增,知false
即当false,即false时,false取到最大值false.
(3)由(2)知点false在直线false的方程为false上,且false
易知椭圆false的左?右顶点分别为false,false,直线false方程为:false,
它与直线false交于点false,则false,
由于false,false都存在,且
false
false
故false于是于是B,Q,F三点共线.
2021.06.
一?填空题
1.已知集合false,则false__________.
2.设false,若复数false是纯虚数,则false__________.
3.不等式false的解集为__________.
4.在false的二项展开式中,常数项是__________.(用数字作答)
5.已知圆锥的主视图为如图所示,则该圆锥的侧面积是__________.
6.已知复数false满足false,则false的取值范围是__________.
7.我校4位同学报考了某大学“强基计划”第1专业组,并顺利通过各项考核,已知4位同学将根据综合成绩和志愿顺序随机地进入数学类?物理学类?计算机类这三个专业中的某一个专业,则这三个专业都有我校学生的录取方法总数有__________种(用数字作答).
8.一个三位数,个位?十位?百位上的数字依次为false,当且仅当false时,称这样的数为“凸数”(如341),则从集合false中取出三个不相同的数组成的凸数个数为___________(用数字作答).
9.(A组题)若false,则false__________.
(B组题)若false,则false__________.
10.(A组题)已知正三棱柱false的侧棱长为4,底面边长为false,且它的六个顶点均在球false的球面上,则false两点的球面距离为__________.
(B组题)已知正三棱柱false的侧棱长为4,底面边长为false,且它的六个顶点均在球false的球面上,则球false的体积为__________.
二?选择题
11.“false”是“false”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
12.设false,且false,则( )
A.false B.false C.false D.false
13.正方体false中,false为线段false上的一个动点,则下列结论错误的是( )
A.false B.false平面false
C.三棱锥false的体积为定值 D.直线false直线false
14.已知false,则false的值不可能为( )
A.false B.false C.false D.false
15.(A组题)已知复数false满足false,复数false满足false或者false,且false对任意false成立,则正整数false的最大值( )
A.6 B.8 C.10 D.12
(B组题)对任意复数false,定义false,其中false是false的共轭复数,对任意复数false,有如下结论:
(1)false
(2)false
(3)false
(4)false
则正确结论的个数是( )
A.4 B.3 C.2 D.1
三?解答题
16.已知false.
(1)若false,求false;
(2)若“false”是“false”的充分不必要条件,求实数false的取值范围.
17.(1)在复数范围内解方程:false为虚数单位);
(2)已知系数为整数的一元二次方程false的一根为false,求false的最小值.
18.如图(1)是一直角墙角,false,墙角的两堵墙面和地面两两互相垂直,ABCD是一块长AB为6米,宽BC为2米的板材,现欲用板材与墙角围成一个直棱柱空间堆放谷物.
(1)若按图(1)方式放置,如何放置板材才能使这个直棱柱空间最大?
(2)由于墙面使用受限,OA面只能使用2米,OB面只能使用4米,此时将矩形板材折叠围成一个直四棱柱空间,如图(2),问如何折叠才能使得这个空间最大?
19.已知如图①,在菱形ABCD中,false且false,false为AD的中点,将false沿BE折起使false,得到如图②所示的四棱锥false,在四棱锥false中,求解下列问题:
(1))求证:BCfalse平面ABE;
(2)(A组题)若P为AC的中点,求二面角false的余弦值.
(B组题)求直线BC与平面ABD所成角的大小.
20.(A组题)阿基米德(公元前287年-公元前212年,古希腊)不仅是著名的哲学家?物理学家,也是著名的数学家.他曾利用“逼近法”得到椭圆的面积等于圆周率false乘以椭圆的长半轴长与短半轴长的乘积在直角坐标系false中,椭圆false的面积为false,两焦点与短轴的一个顶点构成等边三角形,过点false且斜率不为0的直线false与植圆false交于不同的两点A,B.
(1)求椭圆false的标准方程;
(2)求false面积的最大值;
(3)设椭圆E的左?右顶点分别为P,Q,直线PA与直线false交于点false,试问B,Q,F三点是否共线?若共线,请证明;若不共线,请说明理由.
(B组题)已知函数false.
(1)若对于任意false恒成立,求实数false的取值范围;
(2)若对于任意false恒成立,求实数false的取值范围;
(3)若对于任意false成立,求实数false的取值范围.
参考答案
1.false 2.2 3.false 4.20
5.false 6.false 7.36 8.20
9.(A组题)251;(B组题)252 10.(A组题)false;(B组题)false
11.A 12.D 13.D 14.A 15.(A组题)C;(B组题)C
16.(本题满分8分)本题共2小题,每小题4分.
解:(1)由条件,可得false.
当false时,false,故false.
(2)由于false的区间长度不相等,故当“false是false"
的充分不必要条件时,false
解得false,故实数m的取值范围为false
17.(本题满分10分)本题共2小题,每小题5分.
(1)设复数false,则原方程化为false
于是false,解得false
因此原方程的解为false,或falsei.
(2)由条件可得false
解得false,故false,又a,b,c均为整致,故false
因此false
18.(本题满分10分)本题共2小题,每小题5分.
解:(1)设false,则由条件,得false.
从而板材围成的直校柱空间的容积为false
由基本不等式,得false当且仅当false时,等号成立.
因此,放置板材使AOAB为等腰直角三角形,即false(米)时,围成的直梭柱空间的容积最大为18立方米.
(2)设false则由条件,得false
当false时false面积取最大值false
要使将矩形板材折叠围成的直四校柱空间最大,在false时,点P到边AB的距离必须是最大的,即false(M为AB的中点).
此时false
直四校柱空间的容积最大位为false(立方米)
19.(本题满分10分)本题共2小题,4小四5分.
证:(1)在图①中,述接BD,如图所示
因为四边形ABCD为变形.false,所以
false是等边三角形.
因为E为AD中点,所以false.
又false,所以false
在图②中,false,
所以false,即false
因为false,
所以false
又false均在平面false内.
所以false平面false
(2)(false组题)由(1)知,falseBCDE
以false为坐标原点,以射线false分别为false轴,false轴,false轴建立如图所示的空间直角坐标系,则false
false
设平面ABD的一个法向量为false
因为false
由false得false,令false,得false
设平面false的一个法向然为false,
因为false,
由false得false,
令false得false
解:(2)(B组题)由(1)知.false平面false
以E为坐标原点,以射线EB,ED,EA分别为x轴,y轴,z轴,建立如图所示的空间直
角坐标系,false.
false
设平面ABD的一个法向量为false
因为false,
由false得false,
令false,得false
设平面false的一个法向然为false,
因为false,
由false得false,
令false得false
因false,设直线false与平面false所戌角的大小为false,则
false
所以直线BC与平面ABD所成角的大小为false
20.(本题满分12分)(A组题,本题共3小愿,每小题4分)
(1)由题意可得:false,
解得false,false,false,
所以椭圆方程为false.
(2)设直线false的方程为false,false,false,
由false,整理得false,
false,
false,
令false(false),则false,
设false,函数false在区间false单调递增,知false
即当false,即false时,false取到最大值false.
(3)由(2)知点false在直线false的方程为false上,且false
易知椭圆false的左?右顶点分别为false,false,直线false方程为:false,
它与直线false交于点false,则false,
由于false,false都存在,且
false
false
故false于是于是B,Q,F三点共线.
同课章节目录
