2012年中考第一轮复习精品教学案:七、图形变换
文档属性
| 名称 | 2012年中考第一轮复习精品教学案:七、图形变换 |  | |
| 格式 | zip | ||
| 文件大小 | 527.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-19 18:13:44 | ||
图片预览




文档简介
七、图形变换
一、学习目标
1、能识别轴对称图形、中心对称图形。
2、理解平移与旋转的定义和性质。
3、理解轴对称图形与中心对称图形的性质。
4、能利用图形的平移以及旋转变换的知识求作图形、并能设计有关的图案。
5、利用轴对称、平移和旋转的性质进行有关的计算。
二、中考透视
1、判断是否轴对称图形、中心对称图形,指出对称轴或对 称中心。
2、利用轴对称、中心对称作图。
3、用轴对称知识解决折叠等一些问题;
4、将图形旋转某一角度后进行相关的计算与证明。
三、考点再现
1.如图1所示是一张画有小白兔的卡片,卡片正对一面镜子,这张卡片镜子里的影像是下列各图中的( ).
图1 A. B. C. D.
2.(2011年江苏盐都中考模拟)图所示的汽车标志图案中,能用平移变换来分析形成过程的
图案是 ( )
A. B. C . D.
3. (2011湖南邵阳)下列图形不是轴对称图形的是( )
4. (2011浙江省舟山)如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为( )
(A)30° (B)45° (C)90° (D)135°
5.如果将一个图形的各个顶点的横坐标保持不变,纵坐标分别乘以-1,则所得的图案和原图案相比,其变化为( )
A. 关于x轴轴对称 B. 关于y轴轴对称
C. 关于原点中心对称 D. 无法确定
6. (2011山东菏泽)如图所示,已知在三角形纸片ABC中,BC=3, AB=6,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为
A.6 B.3 C. D.
四、典例剖析
例1 (2011四川)下列图形中,是中心对称图形的是 ( )
A. B. C. D.
分析:把图形沿某一直线对折,若直线两旁的部分能够完全重合,则该图形为轴对称图形;若把图形绕某一点旋转 HYPERLINK "http://www./" 后能与自身重合,则该图形为中心对称图形,因此,可知(B)是中心对称图形。另外,边数是奇数的正多边形是轴对称图形,是偶数的既是轴对称图形,又是中心对称图形。(C)可联系正五边形,(D)可联系正三角形。
解: 选B
例2 (2011昭通)如图所示,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3)。
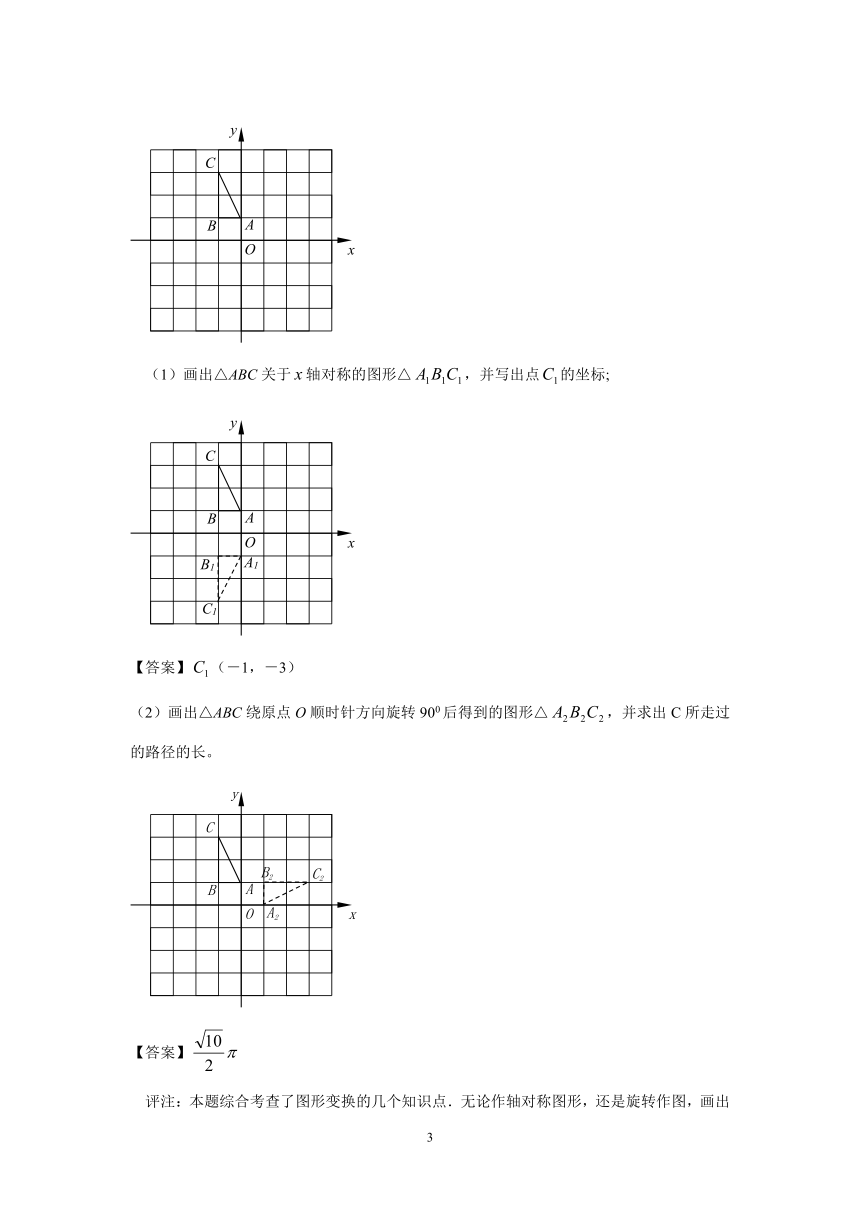
(1)画出△ABC关于轴对称的图形△,并写出点的坐标;
【答案】(-1,-3)
(2)画出△ABC绕原点O顺时针方向旋转900后得到的图形△,并求出C所走过的路径的长。
【答案】
评注:本题综合考查了图形变换的几个知识点.无论作轴对称图形,还是旋转作图,画出关键点变化以后的位置,再连线,是解决这类问题的基本方法.
例3. (2011广东珠海)如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连结AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
(1)解:旋转角的度数为60°.
(2)证明:∵点A、B、C1在一直线上.∴∠ABC1=180°∵∠ABC=∠A1BC1=120°.
∴∠ABA1=CBC1=60°∴∠A1BC=60°,又AB=A1B,所以△ABA1是等边三角形,
∴∠AA1B=∠A1BC1=60°,∴AA1∥BC,∴∠A1AC=∠C,∵△ABC≌△A1BC1,
∴∠C=∠C1,∴∠A1AC=∠C1.
评注:关键是理解旋转的定义和性质,旋转角对应点与旋转中心连线的夹角,所以∠CBC1和∠ABA1都是旋转角,而∠CBC1=180°-120°=60°,所以∠ABA1=60°,而BA=B A1,
所以△ABA1是等边三角形.
五、达标训练
一、选择题
1.(2011山东枣庄)下列图形中,既是轴对称图形,又是中心对称图形的是( )
2. (2011福建龙岩)下列图形中是中心对称图形的是( )
3. (2011 泸州)如图,该图形绕点O按下列角度旋转后,不能与其自身重合的是( )
A、72° B、108° C、144° D、216°
4.(2009 ·山东烟台)如图,数轴上两点表示的数分别为和,点B关于点A的对称点为C,则点C所表示的数为( )
A. B. C. ( http: / / www. / ) D.
5. (2009·四川泸州)如图,P是正△ABC内的一点,若将绕点B旋转到,则的度数是
A.45° B.60°
C.90° D.120°
6..将二次函数y=x2-2x-3的图像向上平移2个单位,再向右平移1个单位,得到的新的图像解析式为( )
A y=(x-2)2-2 B y=(x-2)2+2 C y=(x-2)2-3 D y= (x-2)2+3
7.以下几种位似图形的画法,其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题
1.通过平移把点A(2,-3)移到点(4,-2),按同样的方式,点B(3,1)移动到点,则点的坐标是___________.
2.如图,边长为1的正方形绕点逆时针旋转到正方形,图中阴影部分的面积为______ ______.
3. (2011江苏常州)把棱长为4的正方体分割成29个棱长为整数的正方体(且没有剩余),其中棱长为1的正方体的个数为______.
4. (2011内蒙古赤峰)如图:AD是△ABC的中线,∠ADC=60°,BC=6,把△ABC沿直线AD折叠,点C落在点处,连结B,那么B的长为___________。
5. (2011河北)如图两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A′B′D′的位置,则右图阴影部分的周长为
6.如图,直线与双曲线交于点,将直线向右平移个单位后,与双曲线交于点,与轴交于点. 若,则
7.如图,直线与轴、轴分别交于、两点,把绕点A顺时针旋转90°后得到,则点的坐标是
( http: / / )
三、解答题
1. (2011广东河源)如图4,在平面直角坐标系中,点A(-4,4),点B(-4,0),将△ABO绕原点O按顺时针方向旋转135°得到△A B O。回答下列问题:(直接写结果)
(1)∠AOB= °;
(2)顶点A从开始到经过的路径长为 ;
(3)点的坐标为
2. (2011天津)
在平面直角坐标系中,已知O为坐标原点,点A(3,0), B(0,4) ,以点A为旋转中心,把△ABO顺时针旋转,得△ACD,记旋转角为α,∠ABO=β。
(Ⅰ)如图①,当旋转后点D恰好落在AB边上,求点D的坐标;
(Ⅱ) 如图②,当旋转后满足BC∥x轴时,求α与β之间的数量关系;
(Ⅲ) 当旋转后满足∠AOD=β轴时,求直线CD的解析式(直接写出结果即可)
3.(2009·湖南益阳) 如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长.
小萍同学灵活运用轴对称知识,将图形进行翻折变换,
巧妙地解答了此题.
请按照小萍的思路,探究并解答下列问题:
(1)分别以AB、AC为对称轴,画出△ABD、△ACD的
轴对称图形,D点的对称点为E、F,延长EB、FC
相交于G点,证明四边形AEGF是正方形;
(2)设AD=x,利用勾股定理,建立关于x的方程模型,
求出x的值.
4.(2010四川眉山)如图,Rt△AB C 是由Rt△ABC绕点A顺时针旋转得到的,连结CC 交斜边于点E,CC 的延长线交BB 于点F.
(1)证明:△ACE∽△FBE;
(2)设∠ABC=,∠CAC =,
试探索、满足什么关系时,
△ACE与△FBE是全等三角形,并说明理由.
六、学习感悟
龙山中学 宋庆田 杜君才
七、图形变换 参考答案
考点再现 1---6 CDCCAC
达标训练 一选择1----7 BDBABAD
二填空 1 .(5,2) 2. 1- 3. 24 4. 3 5. 2 6. 12 7. (7,3)
三解答题 1.(1)450;(2);(3)(2,2)
2.解:(Ⅰ)∵点A(3,0),B(0,4),得OA=3,OB=4,
∴在Rt△ABO中,由勾股定理,得AB==5
根据题意,有DA=OA=3
如图①,过点D作DM⊥x轴于点M,
则DN∥OB
∴△ADM∽△ABO
有
得AM=·AO=×3=
DM=·BO=×4=
又OM=OA-AM,得OM=3-=
∴点D的坐标为(,)
(Ⅱ)如图②,由已知,得∠CAB=α,AC=AB
∴∠CBA=∠BCA
∴在ABC中,由∠CBA+∠BCA+∠CAB=180°
得α=180°-2∠CBA
又∵BC∥x轴,得∠OBC=90°
有∠CBA=90°-∠OBA=90°-β
∴α=2β
(Ⅲ)直线CD的解析式为y=-x+4或y=x-4
3.(1)
证明:由题意可得:△ABD≌△ABE,△ACD≌△ACF
∴∠DAB=∠EAB ,∠DAC=∠FAC ,又∠BAC=45°,
∴∠EAF=90°
又∵AD⊥BC
∴∠E=∠ADB=90°∠F=∠ADC=90°
又∵AE=AD,AF=AD
∴AE=AF
∴四边形AEGF是正方形
(2)解:设AD=x,则AE=EG=GF=x
∵BD=2,DC=3
∴BE=2 ,CF=3
∴BG=x-2,CG=x-3
在Rt△BGC中,BG2+CG2=BC2
∴(x-2)2+(x-3)2=52
化简得,x2-5x-6=0
解得x1=6,x2=-1(舍)
所以AD=x=6
4.(1)证明:∵Rt△AB C 是由Rt△ABC绕点A顺时针旋转得到的,
∴AC=AC ,AB=AB ,∠CAB=∠C AB
∴∠CAC =∠BAB
∴∠ACC =∠ABB 又∠AEC=∠FEB
∴△ACE∽△FBE
(2)解:当时,△ACE≌△FBE.
在△ACC中,∵AC=AC ,
∴
在Rt△ABC中,
∠ACC+∠BCE=90°,即,
∴∠BCE=.
∵∠ABC=,
∴∠ABC=∠BCE
∴CE=BE
由(1)知:△ACE∽△FBE,
∴△ACE≌△FBE.
( http: / / www. / )
(第4题)
A
B
C
D
E
y
x
A
B
C
O
y
x
A
B
C
O
A1
B1
C1
y
x
A
B
C
O
A2
B2
C2
A B C D
C
A
O
B
A
B
C
D
HYPERLINK "http://www./"
B
C
A
E
G
D
F
PAGE
9
一、学习目标
1、能识别轴对称图形、中心对称图形。
2、理解平移与旋转的定义和性质。
3、理解轴对称图形与中心对称图形的性质。
4、能利用图形的平移以及旋转变换的知识求作图形、并能设计有关的图案。
5、利用轴对称、平移和旋转的性质进行有关的计算。
二、中考透视
1、判断是否轴对称图形、中心对称图形,指出对称轴或对 称中心。
2、利用轴对称、中心对称作图。
3、用轴对称知识解决折叠等一些问题;
4、将图形旋转某一角度后进行相关的计算与证明。
三、考点再现
1.如图1所示是一张画有小白兔的卡片,卡片正对一面镜子,这张卡片镜子里的影像是下列各图中的( ).
图1 A. B. C. D.
2.(2011年江苏盐都中考模拟)图所示的汽车标志图案中,能用平移变换来分析形成过程的
图案是 ( )
A. B. C . D.
3. (2011湖南邵阳)下列图形不是轴对称图形的是( )
4. (2011浙江省舟山)如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为( )
(A)30° (B)45° (C)90° (D)135°
5.如果将一个图形的各个顶点的横坐标保持不变,纵坐标分别乘以-1,则所得的图案和原图案相比,其变化为( )
A. 关于x轴轴对称 B. 关于y轴轴对称
C. 关于原点中心对称 D. 无法确定
6. (2011山东菏泽)如图所示,已知在三角形纸片ABC中,BC=3, AB=6,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为
A.6 B.3 C. D.
四、典例剖析
例1 (2011四川)下列图形中,是中心对称图形的是 ( )
A. B. C. D.
分析:把图形沿某一直线对折,若直线两旁的部分能够完全重合,则该图形为轴对称图形;若把图形绕某一点旋转 HYPERLINK "http://www./" 后能与自身重合,则该图形为中心对称图形,因此,可知(B)是中心对称图形。另外,边数是奇数的正多边形是轴对称图形,是偶数的既是轴对称图形,又是中心对称图形。(C)可联系正五边形,(D)可联系正三角形。
解: 选B
例2 (2011昭通)如图所示,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3)。
(1)画出△ABC关于轴对称的图形△,并写出点的坐标;
【答案】(-1,-3)
(2)画出△ABC绕原点O顺时针方向旋转900后得到的图形△,并求出C所走过的路径的长。
【答案】
评注:本题综合考查了图形变换的几个知识点.无论作轴对称图形,还是旋转作图,画出关键点变化以后的位置,再连线,是解决这类问题的基本方法.
例3. (2011广东珠海)如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连结AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
(1)解:旋转角的度数为60°.
(2)证明:∵点A、B、C1在一直线上.∴∠ABC1=180°∵∠ABC=∠A1BC1=120°.
∴∠ABA1=CBC1=60°∴∠A1BC=60°,又AB=A1B,所以△ABA1是等边三角形,
∴∠AA1B=∠A1BC1=60°,∴AA1∥BC,∴∠A1AC=∠C,∵△ABC≌△A1BC1,
∴∠C=∠C1,∴∠A1AC=∠C1.
评注:关键是理解旋转的定义和性质,旋转角对应点与旋转中心连线的夹角,所以∠CBC1和∠ABA1都是旋转角,而∠CBC1=180°-120°=60°,所以∠ABA1=60°,而BA=B A1,
所以△ABA1是等边三角形.
五、达标训练
一、选择题
1.(2011山东枣庄)下列图形中,既是轴对称图形,又是中心对称图形的是( )
2. (2011福建龙岩)下列图形中是中心对称图形的是( )
3. (2011 泸州)如图,该图形绕点O按下列角度旋转后,不能与其自身重合的是( )
A、72° B、108° C、144° D、216°
4.(2009 ·山东烟台)如图,数轴上两点表示的数分别为和,点B关于点A的对称点为C,则点C所表示的数为( )
A. B. C. ( http: / / www. / ) D.
5. (2009·四川泸州)如图,P是正△ABC内的一点,若将绕点B旋转到,则的度数是
A.45° B.60°
C.90° D.120°
6..将二次函数y=x2-2x-3的图像向上平移2个单位,再向右平移1个单位,得到的新的图像解析式为( )
A y=(x-2)2-2 B y=(x-2)2+2 C y=(x-2)2-3 D y= (x-2)2+3
7.以下几种位似图形的画法,其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题
1.通过平移把点A(2,-3)移到点(4,-2),按同样的方式,点B(3,1)移动到点,则点的坐标是___________.
2.如图,边长为1的正方形绕点逆时针旋转到正方形,图中阴影部分的面积为______ ______.
3. (2011江苏常州)把棱长为4的正方体分割成29个棱长为整数的正方体(且没有剩余),其中棱长为1的正方体的个数为______.
4. (2011内蒙古赤峰)如图:AD是△ABC的中线,∠ADC=60°,BC=6,把△ABC沿直线AD折叠,点C落在点处,连结B,那么B的长为___________。
5. (2011河北)如图两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A′B′D′的位置,则右图阴影部分的周长为
6.如图,直线与双曲线交于点,将直线向右平移个单位后,与双曲线交于点,与轴交于点. 若,则
7.如图,直线与轴、轴分别交于、两点,把绕点A顺时针旋转90°后得到,则点的坐标是
( http: / / )
三、解答题
1. (2011广东河源)如图4,在平面直角坐标系中,点A(-4,4),点B(-4,0),将△ABO绕原点O按顺时针方向旋转135°得到△A B O。回答下列问题:(直接写结果)
(1)∠AOB= °;
(2)顶点A从开始到经过的路径长为 ;
(3)点的坐标为
2. (2011天津)
在平面直角坐标系中,已知O为坐标原点,点A(3,0), B(0,4) ,以点A为旋转中心,把△ABO顺时针旋转,得△ACD,记旋转角为α,∠ABO=β。
(Ⅰ)如图①,当旋转后点D恰好落在AB边上,求点D的坐标;
(Ⅱ) 如图②,当旋转后满足BC∥x轴时,求α与β之间的数量关系;
(Ⅲ) 当旋转后满足∠AOD=β轴时,求直线CD的解析式(直接写出结果即可)
3.(2009·湖南益阳) 如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长.
小萍同学灵活运用轴对称知识,将图形进行翻折变换,
巧妙地解答了此题.
请按照小萍的思路,探究并解答下列问题:
(1)分别以AB、AC为对称轴,画出△ABD、△ACD的
轴对称图形,D点的对称点为E、F,延长EB、FC
相交于G点,证明四边形AEGF是正方形;
(2)设AD=x,利用勾股定理,建立关于x的方程模型,
求出x的值.
4.(2010四川眉山)如图,Rt△AB C 是由Rt△ABC绕点A顺时针旋转得到的,连结CC 交斜边于点E,CC 的延长线交BB 于点F.
(1)证明:△ACE∽△FBE;
(2)设∠ABC=,∠CAC =,
试探索、满足什么关系时,
△ACE与△FBE是全等三角形,并说明理由.
六、学习感悟
龙山中学 宋庆田 杜君才
七、图形变换 参考答案
考点再现 1---6 CDCCAC
达标训练 一选择1----7 BDBABAD
二填空 1 .(5,2) 2. 1- 3. 24 4. 3 5. 2 6. 12 7. (7,3)
三解答题 1.(1)450;(2);(3)(2,2)
2.解:(Ⅰ)∵点A(3,0),B(0,4),得OA=3,OB=4,
∴在Rt△ABO中,由勾股定理,得AB==5
根据题意,有DA=OA=3
如图①,过点D作DM⊥x轴于点M,
则DN∥OB
∴△ADM∽△ABO
有
得AM=·AO=×3=
DM=·BO=×4=
又OM=OA-AM,得OM=3-=
∴点D的坐标为(,)
(Ⅱ)如图②,由已知,得∠CAB=α,AC=AB
∴∠CBA=∠BCA
∴在ABC中,由∠CBA+∠BCA+∠CAB=180°
得α=180°-2∠CBA
又∵BC∥x轴,得∠OBC=90°
有∠CBA=90°-∠OBA=90°-β
∴α=2β
(Ⅲ)直线CD的解析式为y=-x+4或y=x-4
3.(1)
证明:由题意可得:△ABD≌△ABE,△ACD≌△ACF
∴∠DAB=∠EAB ,∠DAC=∠FAC ,又∠BAC=45°,
∴∠EAF=90°
又∵AD⊥BC
∴∠E=∠ADB=90°∠F=∠ADC=90°
又∵AE=AD,AF=AD
∴AE=AF
∴四边形AEGF是正方形
(2)解:设AD=x,则AE=EG=GF=x
∵BD=2,DC=3
∴BE=2 ,CF=3
∴BG=x-2,CG=x-3
在Rt△BGC中,BG2+CG2=BC2
∴(x-2)2+(x-3)2=52
化简得,x2-5x-6=0
解得x1=6,x2=-1(舍)
所以AD=x=6
4.(1)证明:∵Rt△AB C 是由Rt△ABC绕点A顺时针旋转得到的,
∴AC=AC ,AB=AB ,∠CAB=∠C AB
∴∠CAC =∠BAB
∴∠ACC =∠ABB 又∠AEC=∠FEB
∴△ACE∽△FBE
(2)解:当时,△ACE≌△FBE.
在△ACC中,∵AC=AC ,
∴
在Rt△ABC中,
∠ACC+∠BCE=90°,即,
∴∠BCE=.
∵∠ABC=,
∴∠ABC=∠BCE
∴CE=BE
由(1)知:△ACE∽△FBE,
∴△ACE≌△FBE.
( http: / / www. / )
(第4题)
A
B
C
D
E
y
x
A
B
C
O
y
x
A
B
C
O
A1
B1
C1
y
x
A
B
C
O
A2
B2
C2
A B C D
C
A
O
B
A
B
C
D
HYPERLINK "http://www./"
B
C
A
E
G
D
F
PAGE
9
同课章节目录
