七年级上册数学课件-第六章章末复习 北师版(共23张ppt)
文档属性
| 名称 | 七年级上册数学课件-第六章章末复习 北师版(共23张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-03 19:11:47 | ||
图片预览








文档简介
北师大版·七年级上册
章末复习
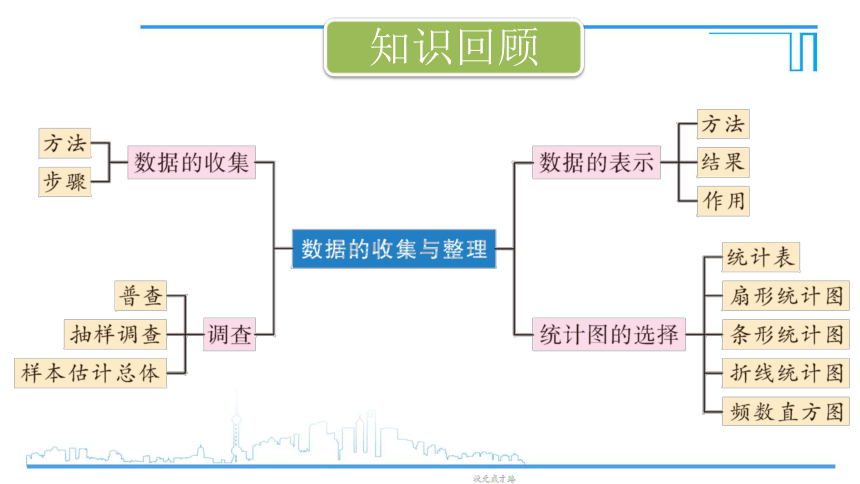
知识回顾
1.普查和抽样调查的概念
为某一特定目的而对所有考察对象进行的全面调查叫做普查.
当不必要或不可能对某一总体进行普查时,我们只要从总体中抽取一部分个体进行调查,这种调查方式称为抽样调查.
下列调查中,调查方式选择合理的是( )
A.为了解福建省初中生每天锻炼所用时间,选择
全面调查
B.为了解福建省《福建新闻》栏目的收视率,选择全面调查
C.为了解神舟飞船设备零件的质量情况,选择抽
样调查
D.为了解一批节能灯的使用寿命,选择抽样调查
D
2.总体、个体、样本的概念
总体是所要考察对象的全体.
样本要指出是在什么样的总体中的一个样本.
个体是总体中的每一个考察对象.
某市今年共有7万名考生参加中考,为了了解这7万名考生的数学成绩,从中抽取了1 000名考生的数学成绩进行统计分析.以下说法正确的有( )
①这种调查采取了抽样调查的方式
②7万名考生是总体
③1 000名考生是总体的一个样本
④每名考生的数学成绩是个体
A.2个 B.3个 C.4个 D.0个
√
7万名考生的数学成绩
1000名考生的数学成绩是总体的一个样本.
√
A
统计图的画法
1.扇形统计图的画法
圆心角度数 = 360°×各部分所占的百分比
下表是某学校学生上学时使用的交通工具
调查统计表.
根据上面的数据,绘制扇形统计图.
解:总人数是 500 + 100 + 160 + 40 = 800(人)
各部分占总体的百分比为:
步行:500÷800×100%=62.5%;
骑自行车:100÷800×100%=12.5%;
乘公共汽车:160÷800×100%=20%;
其他:40÷800×100%=5%.
所对应的扇形圆心角的度数分别为:
步行:360°×62.5%=225°;
骑自行车:360°×12.5%=45°;
乘公共汽车:360°×20%=72°;
其他:360°×5%=18°.
扇形统计图如图所示.
2.频数直方图的画法
为了解上一次七年级数学测验成绩情况,随机抽取了40名学生的成绩进行统计分析.这40名学生的成绩数据如下:
(1)将样本数据适当分组,制作频数直方表:
分组
频数
[50,59]
[60,69]
[70,79]
[80,89]
[90,100]
5
10
15
6
4
(2)根据频数分布表,绘制频数直方图:
分组
频数
[50,59]
[60,69]
[70,79]
[80,89]
[90,100]
5
10
15
6
4
(3)从图可以看出,这40名学生的成绩都分布在什么范围内?分布在哪个范围的人数最多?
从图中可以看出,这40名学生的成绩都分布在50~100分范围内,分数70~80分范围内的人数最多.
条形统计图能清楚地表示出每个项目的具体数目.
折线统计图能清楚地反映事物的变化情况.
扇形统计图能清楚地表示出各部分在总体中所占的百分比.
条形统计图、折线统计图、扇形统计图各有什么特点?
随堂练习
如图表示某校七年级360位同学购买不同品牌计算器人数的扇形统计图,每位同学购买一个计算器,试回答下列问题:
(1)分别求出购买各品牌计算器的人数;
(2)试画出表示购买不同品牌计算器人数的条形统计图.
(1)购买甲品牌计算器的人数:
360×20% = 72(人),
购买乙品牌计算器的人数:
360×30% = 108(人),
购买丙品牌计算器的人数:
360×50% = 180(人).
(2)条形统计图如下图所示.
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
章末复习
知识回顾
1.普查和抽样调查的概念
为某一特定目的而对所有考察对象进行的全面调查叫做普查.
当不必要或不可能对某一总体进行普查时,我们只要从总体中抽取一部分个体进行调查,这种调查方式称为抽样调查.
下列调查中,调查方式选择合理的是( )
A.为了解福建省初中生每天锻炼所用时间,选择
全面调查
B.为了解福建省《福建新闻》栏目的收视率,选择全面调查
C.为了解神舟飞船设备零件的质量情况,选择抽
样调查
D.为了解一批节能灯的使用寿命,选择抽样调查
D
2.总体、个体、样本的概念
总体是所要考察对象的全体.
样本要指出是在什么样的总体中的一个样本.
个体是总体中的每一个考察对象.
某市今年共有7万名考生参加中考,为了了解这7万名考生的数学成绩,从中抽取了1 000名考生的数学成绩进行统计分析.以下说法正确的有( )
①这种调查采取了抽样调查的方式
②7万名考生是总体
③1 000名考生是总体的一个样本
④每名考生的数学成绩是个体
A.2个 B.3个 C.4个 D.0个
√
7万名考生的数学成绩
1000名考生的数学成绩是总体的一个样本.
√
A
统计图的画法
1.扇形统计图的画法
圆心角度数 = 360°×各部分所占的百分比
下表是某学校学生上学时使用的交通工具
调查统计表.
根据上面的数据,绘制扇形统计图.
解:总人数是 500 + 100 + 160 + 40 = 800(人)
各部分占总体的百分比为:
步行:500÷800×100%=62.5%;
骑自行车:100÷800×100%=12.5%;
乘公共汽车:160÷800×100%=20%;
其他:40÷800×100%=5%.
所对应的扇形圆心角的度数分别为:
步行:360°×62.5%=225°;
骑自行车:360°×12.5%=45°;
乘公共汽车:360°×20%=72°;
其他:360°×5%=18°.
扇形统计图如图所示.
2.频数直方图的画法
为了解上一次七年级数学测验成绩情况,随机抽取了40名学生的成绩进行统计分析.这40名学生的成绩数据如下:
(1)将样本数据适当分组,制作频数直方表:
分组
频数
[50,59]
[60,69]
[70,79]
[80,89]
[90,100]
5
10
15
6
4
(2)根据频数分布表,绘制频数直方图:
分组
频数
[50,59]
[60,69]
[70,79]
[80,89]
[90,100]
5
10
15
6
4
(3)从图可以看出,这40名学生的成绩都分布在什么范围内?分布在哪个范围的人数最多?
从图中可以看出,这40名学生的成绩都分布在50~100分范围内,分数70~80分范围内的人数最多.
条形统计图能清楚地表示出每个项目的具体数目.
折线统计图能清楚地反映事物的变化情况.
扇形统计图能清楚地表示出各部分在总体中所占的百分比.
条形统计图、折线统计图、扇形统计图各有什么特点?
随堂练习
如图表示某校七年级360位同学购买不同品牌计算器人数的扇形统计图,每位同学购买一个计算器,试回答下列问题:
(1)分别求出购买各品牌计算器的人数;
(2)试画出表示购买不同品牌计算器人数的条形统计图.
(1)购买甲品牌计算器的人数:
360×20% = 72(人),
购买乙品牌计算器的人数:
360×30% = 108(人),
购买丙品牌计算器的人数:
360×50% = 180(人).
(2)条形统计图如下图所示.
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
